接上篇
CART算法的全称是Classification And Regression Tree，采用的是Gini指数（选Gini指数最小的特征s）作为分裂标准,同时它也是包含后剪枝操作。ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息，但其生成的决策树分支较大，规模较大。为了简化决策树的规模，提高生成决策树的效率，就出现了根据GINI系数来选择测试属性的决策树算法CART。

CART分类与回归树本质上是一样的，构建过程都是逐步分割特征空间，预测过程都是从根节点开始一层一层的判断直到叶节点给出预测结果。只不过分类树给出离散值，而回归树给出连续值(通常是叶节点包含样本的均值），另外分类树基于Gini指数选取分割点，而回归树基于平方误差选取分割点。

6.CART分类树

基尼指数，分类问题中，假设有K个类，样本点属于第k类的概率为 $p_{k}$ ，则概率分布的基尼指数定义为：
$Gini(p)=1-\sum_{k=1}^{K}p_k(1-p_k)=1-\sum_{k=1}^{K}p_k^2$

如果样本集合D根据特征A是否取某一肯值 $a$ 被分割成 $D_1$ 和 $D_2$ 两部分，即：
$D_1={(x,y)∈D|A(x)=a} , D_2=D-D_1$

则在特征A的条件下，集合D的基尼指数定义为：
$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$
基尼指数 $G i n i (D)$ 表示D的不确定性，基尼指数 $G i n i (D, A)$ 表示 $A = a$ 分割后集合D的不确定性，基尼指数值越大，样本集合的不确定性就越大，与熵类似。

CART分类树算法逻辑，《统计学习方法》李航，P70-71页：在这里插入图片描述

按传入数据最后一列y值求gini指数

# 计算传入数据的Gini指数
def calcGini(dataSet):#dataSet=dataSet[list(dataSet[:,0]=='青年')]# 获得y中分类标签的唯一值y_lables = np.unique(dataSet[: , -1])y_counts=len(dataSet) # y总数据条数y_p={}             # y中每一个分类的概率，字典初始化为空，y分类数是不定的，按字典存储更方便取值gini=1.0for y_lable in y_lables:y_p[y_lable]=len(dataSet[dataSet[:, -1]==y_lable])/y_counts  # y中每一个分类的概率（其实就是频率）gini-=y_p[y_lable]**2return gini

切分数据，每一列x找一个最优的特征进行划分

#划分数据集
def splitDataSet(dataSet, i, value,types=1):#dataSet[list(dataSet[:,0]!='青年')]if types==1: # 使用此列特征中的value进行划分数据subDataSet=dataSet[list(dataSet[:,i]==value)]  # 按照数据x第i列==value即可判断，不需要像《机器学习实战》书里写的那么复杂subDataSet = np.array(subDataSet)           # 强制转换为array类型elif types==2: # 使用此列特征中的不等于value的进行划分数据subDataSet=dataSet[list(dataSet[:,i]!=value)]  # 按照数据x第i列==value即可判断，不需要像《机器学习实战》书里写的那么复杂subDataSet = np.array(subDataSet)           # 强制转换为array类型return subDataSet ,len(subDataSet)

遍历所有x特征列中的所有特征，寻找最优划分特征

# 计算Gini指数，选择最好的特征划分数据集，即返回最佳特征下标及传入数据集各列的Gini指数
def chooseBestFeature(dataSet,types='Gini'):numTotal=dataSet.shape[0]              # 记录本数据集总条数numFeatures = len(dataSet[0]) - 1      # 最后一列为y，计算x特征列数bestFeature = -1                       # 初始化参数，记录最优特征列i，下标从0开始columnFeaGini={}                       # 初始化参数，记录每一列x的每一种特征的基尼 Gini(D,A)for i in range(numFeatures):           # 遍历所有x特征列# i=2prob = {}                          # 按x列计算各个分类的概率featList = list(dataSet[:,i])      # 取这一列x中所有数据，转换为list类型prob=dict(Counter(featList))       # 使用Counter函数计算这一列x各特征数量for value in prob.keys():          # 循环这一列的特征，计算H(D|A)# value='是'feaGini = 0.0bestFlag = 1.00001  # 对某一列x中，会出现x=是，y=是的特殊情况，这种情况下按“是”、“否”切分数据得到的Gini都一样，设置此参数将所有特征都乘以一个比1大一点点的值，但按某特征划分Gini为0时，设置为1subDataSet1,sublen1 = splitDataSet(dataSet, i, value, 1)  # 获取切分后的数据subDataSet2,sublen2 = splitDataSet(dataSet, i, value, 2)if (sublen1/numTotal) * calcGini(subDataSet1)==0: # 判断按此特征划分Gini值是否为0（全部为一类）bestFlag = 1 feaGini += (sublen1/numTotal) * calcGini(subDataSet1) + (sublen2/numTotal) * calcGini(subDataSet2)columnFeaGini['%d_%s'%(i,value)]=feaGini*bestFlagbestFeature=min(columnFeaGini,key=columnFeaGini.get) # 找到最小的Gini指数益对应的数据列return bestFeature,columnFeaGini

CART分类树创建主函数，递归调用产生整颗决策树

def createTree(dataSet,features,types='Gini'):"""输入：训练数据集D，特征集A，阈值ε输出：决策树T"""y_lables = np.unique(dataSet[: , -1])#1、如果数据集D中的所有实例都属于同一类label（Ck），则T为单节点树，并将类label（Ck）作为该结点的类标记，返回Tif len(set(y_lables)) == 1:return y_lables[0]#2、若特征集A=空，则T为单节点，并将数据集D中实例树最大的类label（Ck）作为该节点的类标记，返回Tif len(dataSet[0]) == 1:labelCount = {}labelCount=dict(Counter(y_lables))return max(labelCount,key=labelCount.get)#3、否则，按CART算法就计算特征集A中各特征对数据集D的Gini，选择Gini指数最小的特征bestFeature（Ag）进行划分bestFeature,columnFeaGini=chooseBestFeature(dataSet,types) bestFeatureLable = features[int(bestFeature.split('_')[0])]    #最佳特征decisionTree = {bestFeatureLable:{}}        #构建树，以Gini指数最小的特征bestFeature为子节点del(features[int(bestFeature.split('_')[0])])                  #该特征已最为子节点使用，则删除，以便接下来继续构建子树#使用beatFeature进行划分，划分产生2各节点，成树T，返回Ty_lables_split=dataSet[list(dataSet[:,int(bestFeature.split('_')[0])]==bestFeature.split('_')[1])][:,-1] # 获取按此划分后y数据列表y_lables_grp=dict(Counter(y_lables_split)) # 统计最优划分应该属于哪个i叶子节点“是”、“否”y_leaf=max(y_lables_grp,key=y_lables_grp.get) # 获得划分后出现概率最大的y分类decisionTree[bestFeatureLable][bestFeature.split('_')[1]]= y_leaf # 设定左枝叶子值#4、删除此最优划分数据x列，使用其他x列数据，递归地调用步1-3，得到子树Ti，返回TidataSetNew= np.delete(dataSet,int(bestFeature.split('_')[0]),axis=1) # 删除此最优划分x列，使用剩余的x列进行数据划分subFeatures = features[:]# 判断右枝类型，划分后的左右枝“是”、“否”是不一定的，所以这里进行判断y1=y_lables[0] # CART树y只能有2个分类y2=y_lables[1] if y_leaf==y1:decisionTree[bestFeatureLable][y2]= {}decisionTree[bestFeatureLable][y2] = createTree(dataSetNew, subFeatures,types)elif y_leaf==y2:decisionTree[bestFeatureLable][y1]= {}decisionTree[bestFeatureLable][y1] = createTree(dataSetNew, subFeatures,types)return decisionTree

cart决策树结果验证，计算结果与《统计学习方法》李航，P71页一致。
在这里插入图片描述

cart决策树及画图结果：
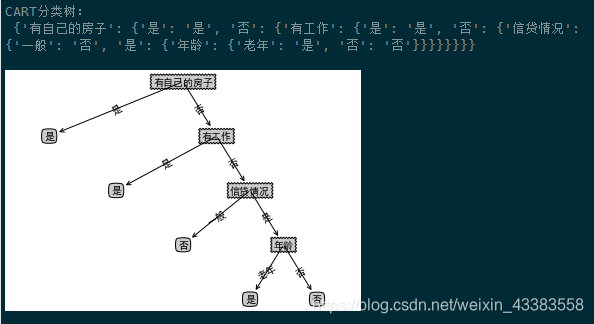
在这里插入图片描述

7.CART回归树

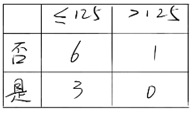
CART回归树样本空间细分成若干子空间，子空间内样本的输出y(连续值)的均值即为该子空间内的预测值。故对于输入X为一维时，预测结果可表示为阶梯函数。
评估方式采用平方误差：yi 属于某个数据集，c为该数据上输出向量y的均值。
$err=\sum(y_i-c)$

CART回归树算法逻辑，《统计学习方法》李航，P69页：
在这里插入图片描述

最小二乘损失

def err(dataSet):#return sum((dataSet[:,-1]- dataSet[:,-1].mean())**2) # 最原始的写法return np.var(dataSet[:,-1])*dataSet.shape[0]  #均方差*数据总条数

划分数据集，按出入的数据列fea，数据值value将数据划分为两部分

def splitDataSet(dataSet, fea, value):dataSet1=dataSet[dataSet[:,fea]<=value]dataSet2=dataSet[dataSet[:,fea]>value]return dataSet1,dataSet2

#选择最好的特征划分数据集，min_sample每次划分后每部分最少的数据条数，epsilon误差下降阈值，值越小划分的决策树越深

def chooseBestFeature(dataSet,min_sample=4,epsilon=0.5):features=dataSet.shape[1]-1   # x特征列数量sErr=err(dataSet) # 整个数据集的损失minErr=np.infbestColumn = 0 # 划分最优列bestValue = 0  # 划分最优的值nowErr=0       # 当前平方误差if len(np.unique(dataSet[:,-1].T.tolist())) == 1: # 数据全是一类的情况下 返回return None, np.mean(dataSet[:,-1])for fea in range(0,features): # 按x特征列循环for row in range(0,dataSet.shape[0]): # 遍历每行数据，寻找最优划分dataSet1,dataSet2=splitDataSet(dataSet, fea,dataSet[row,fea]) # 获得切分后的数据if len(dataSet1) < min_sample or len(dataSet2) < min_sample:  # 按行遍历时总会有一些划分得到的集合不满足最小数据条数约束，跳过此类划分continuenowErr=err(dataSet1)+err(dataSet2) # 计算当前划分的平方误差#print('fea:',fea,'row:',row,'datavalue',dataSet[row,fea],'nowErr',nowErr)if nowErr<minErr: # 判断获得最优切分值minErr=nowErrbestColumn=feabestValue=dataSet[row,fea]#print('fea',fea,'minErr',minErr,'bestColumn',bestColumn,'bestValue',bestValue)if (sErr - minErr) < epsilon: # 当前误差下降较小时，返回return None, np.mean(dataSet[:,-1])# 当前最优划分集合dataSet1,dataSet2=splitDataSet(dataSet, bestColumn,bestValue)if len(dataSet1) < min_sample or len(dataSet2) < min_sample: # 如果划分的数据集很小，返回return None, np.mean(dataSet[:,-1])return bestColumn,bestValue

CART回归树控制主函数，递归调用产生整颗树

def createTree(dataSet):"""输入：训练数据集D，特征集A，阈值ε输出：决策树T"""bestColumn,bestValue=chooseBestFeature(dataSet)if bestColumn == None:  # 所有列均遍历完毕，返回return bestValueretTree = {}  # 决策树 retTree['spCol'] = bestColumn # 最优分割列retTree['spVal'] = bestValue  # 最优分割值lSet, rSet = splitDataSet(dataSet, bestColumn,bestValue) # 按当前最优分割列级值划分为左右2枝retTree['left'] = createTree(lSet)  # 迭代继续划分左枝retTree['right'] = createTree(rSet) # 迭代继续划分右枝return retTree

CART回归树输出结果：
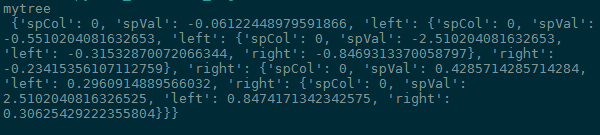
在这里插入图片描述

CART分类树完整代码：

# -*- coding: utf-8 -*-
"""@Time    : 2018/11/16 09:58@Author  : hanzi5@Email   : hanzi5@yeah.net@File    : cart_classification.py@Software: PyCharm
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
from collections import Countermatplotlib.rcParams['font.family']='SimHei'  # 用来正常显示中文
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")# 计算传入数据的Gini指数
def calcGini(dataSet):#dataSet=dataSet[list(dataSet[:,0]=='青年')]# 获得y中分类标签的唯一值y_lables = np.unique(dataSet[: , -1])y_counts=len(dataSet) # y总数据条数y_p={}             # y中每一个分类的概率，字典初始化为空，y分类数是不定的，按字典存储更方便取值gini=1.0for y_lable in y_lables:y_p[y_lable]=len(dataSet[dataSet[:, -1]==y_lable])/y_counts  # y中每一个分类的概率（其实就是频率）gini-=y_p[y_lable]**2return gini# 计算Gini指数的另一种写法
def getGini(dataSet):# 计算基尼指数c = Counter(dataSet[:,-1])ret=1 - sum([(val / dataSet[:,-1].shape[0]) ** 2 for val in c.values()])return ret#划分数据集
def splitDataSet(dataSet, i, value,types=1):#dataSet[list(dataSet[:,0]!='青年')]if types==1: # 使用此列特征中的value进行划分数据subDataSet=dataSet[list(dataSet[:,i]==value)]  # 按照数据x第i列==value即可判断，不需要像《机器学习实战》书里写的那么复杂subDataSet = np.array(subDataSet)           # 强制转换为array类型elif types==2: # 使用此列特征中的不等于value的进行划分数据subDataSet=dataSet[list(dataSet[:,i]!=value)]  # 按照数据x第i列==value即可判断，不需要像《机器学习实战》书里写的那么复杂subDataSet = np.array(subDataSet)           # 强制转换为array类型return subDataSet ,len(subDataSet)# 计算Gini指数，选择最好的特征划分数据集，即返回最佳特征下标及传入数据集各列的Gini指数
def chooseBestFeature(dataSet,types='Gini'):numTotal=dataSet.shape[0]              # 记录本数据集总条数numFeatures = len(dataSet[0]) - 1      # 最后一列为y，计算x特征列数bestFeature = -1                       # 初始化参数，记录最优特征列i，下标从0开始columnFeaGini={}                       # 初始化参数，记录每一列x的每一种特征的基尼 Gini(D,A)for i in range(numFeatures):           # 遍历所有x特征列# i=2prob = {}                          # 按x列计算各个分类的概率featList = list(dataSet[:,i])      # 取这一列x中所有数据，转换为list类型prob=dict(Counter(featList))       # 使用Counter函数计算这一列x各特征数量for value in prob.keys():          # 循环这一列的特征，计算H(D|A)# value='是'feaGini = 0.0bestFlag = 1.00001  # 对某一列x中，会出现x=是，y=是的特殊情况，这种情况下按“是”、“否”切分数据得到的Gini都一样，设置此参数将所有特征都乘以一个比1大一点点的值，但按某特征划分Gini为0时，设置为1subDataSet1,sublen1 = splitDataSet(dataSet, i, value, 1)  # 获取切分后的数据subDataSet2,sublen2 = splitDataSet(dataSet, i, value, 2)if (sublen1/numTotal) * calcGini(subDataSet1)==0: # 判断按此特征划分Gini值是否为0（全部为一类）bestFlag = 1 feaGini += (sublen1/numTotal) * calcGini(subDataSet1) + (sublen2/numTotal) * calcGini(subDataSet2)columnFeaGini['%d_%s'%(i,value)]=feaGini*bestFlagbestFeature=min(columnFeaGini,key=columnFeaGini.get) # 找到最小的Gini指数益对应的数据列return bestFeature,columnFeaGinidef createTree(dataSet,features,types='Gini'):"""输入：训练数据集D，特征集A，阈值ε输出：决策树T"""y_lables = np.unique(dataSet[: , -1])#1、如果数据集D中的所有实例都属于同一类label（Ck），则T为单节点树，并将类label（Ck）作为该结点的类标记，返回Tif len(set(y_lables)) == 1:return y_lables[0]#2、若特征集A=空，则T为单节点，并将数据集D中实例树最大的类label（Ck）作为该节点的类标记，返回Tif len(dataSet[0]) == 1:labelCount = {}labelCount=dict(Counter(y_lables))return max(labelCount,key=labelCount.get)#3、否则，按CART算法就计算特征集A中各特征对数据集D的Gini，选择Gini指数最小的特征bestFeature（Ag）进行划分bestFeature,columnFeaGini=chooseBestFeature(dataSet,types) bestFeatureLable = features[int(bestFeature.split('_')[0])]    #最佳特征decisionTree = {bestFeatureLable:{}}        #构建树，以Gini指数最小的特征bestFeature为子节点del(features[int(bestFeature.split('_')[0])])                  #该特征已最为子节点使用，则删除，以便接下来继续构建子树#使用beatFeature进行划分，划分产生2各节点，成树T，返回Ty_lables_split=dataSet[list(dataSet[:,int(bestFeature.split('_')[0])]==bestFeature.split('_')[1])][:,-1] # 获取按此划分后y数据列表y_lables_grp=dict(Counter(y_lables_split)) # 统计最优划分应该属于哪个i叶子节点“是”、“否”y_leaf=max(y_lables_grp,key=y_lables_grp.get) # 获得划分后出现概率最大的y分类decisionTree[bestFeatureLable][bestFeature.split('_')[1]]= y_leaf # 设定左枝叶子值#4、删除此最优划分数据x列，使用其他x列数据，递归地调用步1-3，得到子树Ti，返回TidataSetNew= np.delete(dataSet,int(bestFeature.split('_')[0]),axis=1) # 删除此最优划分x列，使用剩余的x列进行数据划分subFeatures = features[:]# 判断右枝类型，划分后的左右枝“是”、“否”是不一定的，所以这里进行判断y1=y_lables[0] # CART树y只能有2个分类y2=y_lables[1] if y_leaf==y1:decisionTree[bestFeatureLable][y2]= {}decisionTree[bestFeatureLable][y2] = createTree(dataSetNew, subFeatures,types)elif y_leaf==y2:decisionTree[bestFeatureLable][y1]= {}decisionTree[bestFeatureLable][y1] = createTree(dataSetNew, subFeatures,types)return decisionTree####以下是用来画图的完全复制的《机器学习实战》第三章的内容，不感兴趣的可以略过#############################################
def getNumLeafs(myTree):numLeafs = 0firstStr = list(myTree.keys())[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodesnumLeafs += getNumLeafs(secondDict[key])else:   numLeafs +=1return numLeafsdef getTreeDepth(myTree):maxDepth = 0firstStr = list(myTree.keys())[0]#myTree.keys()[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodesthisDepth = 1 + getTreeDepth(secondDict[key])else:   thisDepth = 1if thisDepth > maxDepth: maxDepth = thisDepthreturn maxDepthdef plotNode(nodeTxt, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )def plotMidText(cntrPt, parentPt, txtString):xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split onnumLeafs = getNumLeafs(myTree)  #this determines the x width of this tree#depth = getTreeDepth(myTree)firstStr = list(myTree.keys())[0]#myTree.keys()[0]     #the text label for this node should be thiscntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)plotMidText(cntrPt, parentPt, nodeTxt)plotNode(firstStr, cntrPt, parentPt, decisionNode)secondDict = myTree[firstStr]plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalDfor key in secondDict.keys():if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   plotTree(secondDict[key],cntrPt,str(key))        #recursionelse:   #it's a leaf node print the leaf nodeplotTree.xOff = plotTree.xOff + 1.0/plotTree.totalWplotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dictdef createPlot(myTree):fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses plotTree.totalW = float(getNumLeafs(myTree))plotTree.totalD = float(getTreeDepth(myTree))plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;plotTree(myTree, (0.5,1.0), '')plt.show()
####画图结束，不感兴趣的可以略过#############################################if __name__ == "__main__":  #读入数据，《统计学习方法》李航，P59，表5.1df_data=pd.read_csv('D:/python_data/loan_application.csv')features = list(df_data.columns[1:-1]) # x的表头dataSet=np.array(df_data.values[:,1:]) # 数据处理为numpy.array类型，其实pandas.Dataframe类型更方便计算# 结果验证，计算结果与《统计学习方法》李航，P71页一致。bestFeature,columnFeaGini=chooseBestFeature(dataSet,'Gini')print('\nbestFeature:',bestFeature,'\nGini(D,A):',columnFeaGini)dt_Gini = createTree(dataSet, features,'Gini')   #建立决策树，CART分类树print( 'CART分类树：\n',dt_Gini)# 画出决策树createPlot(dt_Gini)

CART回归树完整代码：

# -*- coding: utf-8 -*-
"""@Time    : 2018/11/19 14:45@Author  : hanzi5@Email   : hanzi5@yeah.net@File    : cart_reg.py@Software: PyCharm
"""import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 最小二乘损失
def err(dataSet):#return sum((dataSet[:,-1]- dataSet[:,-1].mean())**2) # 最原始的写法return np.var(dataSet[:,-1])*dataSet.shape[0]  #均方差*数据总条数#划分数据集，按出入的数据列fea，数据值value将数据划分为两部分
def splitDataSet(dataSet, fea, value):dataSet1=dataSet[dataSet[:,fea]<=value]dataSet2=dataSet[dataSet[:,fea]>value]return dataSet1,dataSet2# 选择最好的特征划分数据集，min_sample每次划分后每部分最少的数据条数，epsilon误差下降阈值，值越小划分的决策树越深
def chooseBestFeature(dataSet,min_sample=4,epsilon=0.5):features=dataSet.shape[1]-1   # x特征列数量sErr=err(dataSet) # 整个数据集的损失minErr=np.infbestColumn = 0 # 划分最优列bestValue = 0  # 划分最优的值nowErr=0       # 当前平方误差if len(np.unique(dataSet[:,-1].T.tolist())) == 1: # 数据全是一类的情况下 返回return None, np.mean(dataSet[:,-1])for fea in range(0,features): # 按x特征列循环for row in range(0,dataSet.shape[0]): # 遍历每行数据，寻找最优划分dataSet1,dataSet2=splitDataSet(dataSet, fea,dataSet[row,fea]) # 获得切分后的数据if len(dataSet1) < min_sample or len(dataSet2) < min_sample:  # 按行遍历时总会有一些划分得到的集合不满足最小数据条数约束，跳过此类划分continuenowErr=err(dataSet1)+err(dataSet2) # 计算当前划分的平方误差#print('fea:',fea,'row:',row,'datavalue',dataSet[row,fea],'nowErr',nowErr)if nowErr<minErr: # 判断获得最优切分值minErr=nowErrbestColumn=feabestValue=dataSet[row,fea]#print('fea',fea,'minErr',minErr,'bestColumn',bestColumn,'bestValue',bestValue)if (sErr - minErr) < epsilon: # 当前误差下降较小时，返回return None, np.mean(dataSet[:,-1])# 当前最优划分集合dataSet1,dataSet2=splitDataSet(dataSet, bestColumn,bestValue)if len(dataSet1) < min_sample or len(dataSet2) < min_sample: # 如果划分的数据集很小，返回return None, np.mean(dataSet[:,-1])return bestColumn,bestValuedef createTree(dataSet):"""输入：训练数据集D，特征集A，阈值ε输出：决策树T"""bestColumn,bestValue=chooseBestFeature(dataSet)if bestColumn == None:  # 所有列均遍历完毕，返回return bestValueretTree = {}  # 决策树 retTree['spCol'] = bestColumn # 最优分割列retTree['spVal'] = bestValue  # 最优分割值lSet, rSet = splitDataSet(dataSet, bestColumn,bestValue) # 按当前最优分割列级值划分为左右2枝retTree['left'] = createTree(lSet)  # 迭代继续划分左枝retTree['right'] = createTree(rSet) # 迭代继续划分右枝return retTreeif __name__ == '__main__':# 使用sin函数随机产生x，y数据X_data_raw = np.linspace(-3, 3, 50)np.random.shuffle(X_data_raw)  # 随机打乱数据y_data = np.sin(X_data_raw)    # 产生数据yx = np.transpose([X_data_raw]) # 将x进行转换y = y_data + 0.1 * np.random.randn(y_data.shape[0]) # 产生数据y，增加随机噪声dataSet=np.column_stack((x,y.reshape((-1,1))))      # 将x与y进行合并#    data=pd.read_table('D:/python_data/ex0.txt',header=None)
#    dataSet=data.valuesmytree=createTree(dataSet) print('mytree\n',mytree)

注意，以上实现的CART分类树与CART回归树均没有进行减枝操作。

参考资料：
1、Machine-Learning-With-Python
2、《机器学习实战》Peter Harrington著
3、《机器学习》西瓜书，周志华著
4、斯坦福大学公开课：机器学习课程
5、机器学习视频，邹博
6、《统计学习方法》李航
7、《机器学习实战》基于信息论的三种决策树算法(ID3,C4.5,CART)
8、分类回归——CART分类与回归以及Python实现