1.Numpy的核心array对象以及创建array的方法

Numpy的核心数据结构，就叫做array就是数组，array对象可以是一维数组，也可以是多维数组；
Python的List也可以实现相同的功能，但是array比List的优点在于性能好、包含数组元数据信息、大量的便捷函数；
Numpy成为事实上的Scipy、Pandas、Scikit-Learn、Tensorflow、PaddlePaddle等框架的“通用底层语言”
Numpy的array和Python的List的一个区别，是它元素必须都是同一种数据类型，比如都是数字int类型，这也是Numpy高性能的一个原因；

array本身的属性

shape：返回一个元组，表示array的维度x.shape
ndim：一个数字，表示array的维度的数目
size：一个数字，表示array中所有数据元素的数目
dtype：array中元素的数据类型

创建array的方法

从Python的列表List和嵌套列表创建array
使用预定函数arange、ones/ones_lik（全为1）e、zeros/zeros_like（全为0）、empty/empty_like（全为空）、full/full_like（指定数值）、eye（单位矩阵）等函数创建
生成随机数的np.random模块构建

1.1创建array的便捷函数

np.arange(10)

#2开始8结束，步长为2
np.arange(2, 10, 2

)

#跟x形状相同，里面变成1
np.ones_like(x)

使用random模块生成随机数的数组

#三维数组
np.random.randn(3, 2, 4)

1.2array本身支持的大量操作和函数

直接逐元素的加减乘除等算数操作
更好用的面向多维的数组索引
求sum/mean等聚合函数
线性代数函数，比如求解逆矩阵、求解方程组

A = np.arange(10).reshape(2,5)

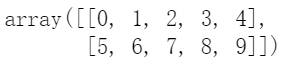
A+1

2.Numpy对数组按索引查询

三种索引方法：

基础索引
神奇索引
布尔索引

2.1基础索引（切片）

行列用都逗号分隔，：表示从哪到n-1的位置

一维数组

不包括-1

二维数组

#-1是最后一行，-是最后

# 筛选多行，：右边不包括-1
X[:-1]

# 筛选多行，然后筛选多列，右边不包括2，4
X[:2, 2:4]

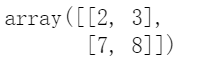
# 筛选所有行，然后筛选多列
X[:, 2]

2.2神奇索引（用整数数组进行的索引，叫神奇索引）数组里面套数组

一维数组

对应位置和形式

indexs = np.array([[0, 2], [1, 3]]) 两行两列对应四个位置索引
x[indexs]

。。。。。。。。。。。。。。。。。。。。。。。。。。。。

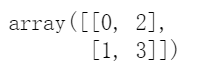
# 随机生成1到100之间的，10个数字
arr = np.random.randint(1,100,10)

# arr.argsort()会返回排序后的索引index
# 取最大值对应的3个下标
arr.argsort()[-3:]

arr[arr.argsort()[-3:]]

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

二维数组就是有行有列了，用逗号分割

X = np.arange(20).reshape(4, 5)

# 筛选多行，列可以省略，逗号是位置
X[[0, 2]]

# 筛选多列，行不能省略，:列可省略
X[:, [0,2,3]]

# 同时指定行列-列表-----------指定了行列可以定位了
# 返回的是[(0,1), (2,3), (3,4)]位置的数字
X[[0, 2, 3], [1, 3, 4]]

2.3布尔索引

一维数组

# 实例：把一维数组进行01化处理
# 比如把房价数字，变成“高房价”为1，“低房价”为0
x[x<=5] = 0
x[x>5] = 1

x = np.arange(10)
x[x < 5] += 20

二维数组

X = np.arange(20).reshape(4,5)

X > 5

# X>5的boolean数组，既有行，又有列，，，，，降维
# 因此返回的是（行，列）一维结果
X[X>5]

。。。。。。。。。。。。。。。。。。。。。。。。

怎样把第3列大于5的行筛选出来

X[:, 3]>5

# 这里是按照行进行的筛选
X[X[:, 3]>5]

。。。。。。。。。。。。。。。。。。。。。。。。。。。。

条件的组合

# 注意，每个条件都得加小括号
condition = (x%2==0) | (x>7)
condition

3.Numpy常用random随机函数汇总

3.1 rand(d0, d1, ..., dn)

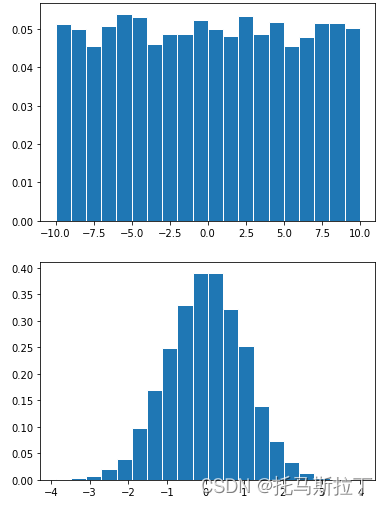
返回数据在[0, 1)之间，具有均匀分布

均匀分布

若连续型随机变量具有概率密度

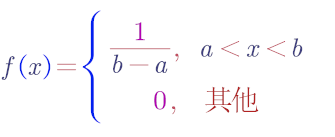
则称X在区间（a，b）上服从均匀分布.记为X～U（a，b）

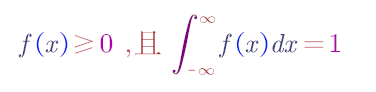
在区间（a，b）上服从均匀分布的随机变量 X，落在区间（a，b）中任意等长度的子区间内的可能性是相同的.

或者它落在（a，b）的子区间内的概率只依赖于子区间的长度而与子区间的位置无关.

事实上，对于任一长度l的子区间（c，c+l），a≤c<c＋l≤b，

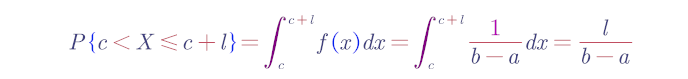
X的分布函数为

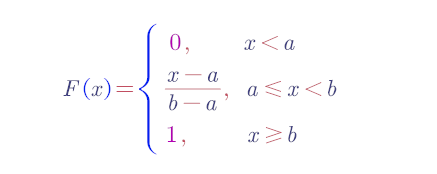
f（x）及F（x）的图形

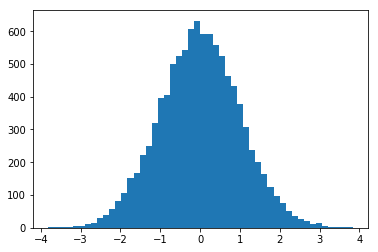
3.2 randn(d0, d1, ..., dn)

返回数据具有标准正态分布（均值0，方差1）

a = 0并且b = 1，所得分布U（0,1）称为标准均匀分布。

正态分布的平均数为μ，标准差为σ；不同的正态分布可能有不同的μ值和σ值，正态分布曲线形态因此不同。

标准正态分布平均数μ=0，标准差σ=1，μ和σ都是固定值；标准正态分布曲线形态固定。

(2)联系：正态分布可以通过标准化处理，转化为标准正态分布。具体方法是使用z=(X-μ)/σ将原始数据转化为标准分数。

正态分布：

正态分布（Normal distribution）又名高斯分布（Gaussiandistribution），若随机变量X服从一个数学期望为μ、方差为σ2的高斯分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布。当μ=0，σ=1时，正态分布就成为标准正态分布N（0，1)。概率密度函数为：

正态分布的密度函数的特点是：关于μ对称，并在μ处取最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点，形状呈现中间高两边低，图像是一条位于x轴上方的钟形曲线。

3.3 randint(low[, high, size, dtype])

生成随机整数，包含low，不包含high
如果high不指定，则从[0, low)中生成数字

3.4random([size])

生成[0.0, 1.0)的随机数

3.5. choice(a[, size, replace, p])

a是一维数组，从它里面生成随机结果

# 这时候，a是数字，则从range(5)中生成，size为3
np.random.choice(5, 3)

# 这时候，a是数组，从里面随机取出数字
np.random.choice([2, 3, 6, 7, 9], 3)

3.6 shuffle(x)

把一个数组x进行随机排列

# 如果数组是多维的，则只会在第一维度打散数据

np.random.shuffle(a)

3.7permutation(x)

把一个数组x进行随机排列，或者数字的全排列

# 注意，这里不会更改原来的arr，会返回一个新的copy

# 这时候，生成range(10)的随机排列
np.random.permutation(10)

np.random.permutation(arr)

3.8normal([loc, scale, size])普通正态分布

按照平均值loc和方差scale生成高斯分布的数字

态分布（Normal distribution），也称“常态分布”，又名高斯分布

np.random.normal(1, 10, 10)

3.9uniform([low, high, size])普通均匀分布

在[low, high)之间生成均匀分布的数字

.。。。。。。。。。。。。。。。

对数组加入随机噪声

rand均匀分布

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0) 用于返回指定区间等间隔的数组。

。。。。。。。。。。。。。。。。

4.Numpy的数学统计函数

。。。。。。。。。。。。。

机器学习将数据进行标准化

array([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]])

arr如果对应到现实世界的一种解释：

行：每行对应一个样本数据
列：每列代表样本的一个特征

数据标准化：

对于机器学习、神经网络来说，不同列的量纲应该相同，训练收敛的更快；
比如商品的价格是0到100元、销量是1万到10万个，这俩数字没有可比性，因此需要先都做标准化；
不同列代表不同的特征，因此需要axis=0做计算
标准化一般使用A = (A - mean(A, axis=0)) / std(A, axis=0)公式进行

计算分子，注意(3行）每行都会分别减去mean[4., 5., 6., 7.]，这叫做numpy的广播

5.怎样给数组增加一个维度

背景：
很多数据计算都是二维或三维的，对于一维的数据输入为了形状匹配，经常需升维变成二维

需要：
在不改变数据的情况下，添加数组维度；（注意观察这个例子，维度变了，但数据不变）
原始数组：一维数组arr=[1,2,3,4]，其shape是(4, )，取值分别为arr[0],arr[1],arr[2],arr[3]
变形数组：二维数组arr[[1,2,3,4]]，其shape实(1,4), 取值分别为a[0,0],a[0,1],a[0,2],a[0,3]

实操：
经常需要在纸上手绘数组的形状，来查看不同数组是否形状匹配，是否需要升维降维

3种方法：

np.newaxis：关键字，使用索引的语法给数组添加维度
np.expand_dims(arr, axis)：方法，和np.newaxis实现一样的功能，给arr在axis位置添加维度
np.reshape(a, newshape)：方法，给一个维度设置为1完成升维

5.1np.newaxis

注意：np.newaxis其实就是None的别名np.newaxis == None

给一维向量添加一个行维度

arr[np.newaxis, :]

数据现在是一行*五列，数据本身没有增减，只是多了一级括号

给一维向量添加一个列维度

arr[:, np.newaxis]

5.2np.expand_dims(arr, axis)

np.expand_dims(arr, axis=0)

np.expand_dims(arr, axis=1)

5.3np.reshape(a, newshape)

np.reshape(arr, (1, -1))意为(1, 5) -1是最后一个=5/1

np.reshape(arr, (-1, 1))意为(5, 1)

6.Numpy非常重要有用的数组合并操作

背景：在给机器学习准备数据的过程中，经常需要进行不同来源的数据合并的操作。

两类场景：

给已有的数据添加多行，比如增添一些样本数据进去；
给已有的数据添加多列，比如增添一些特征进去；

以下操作均可以实现数组合并：

np.concatenate(array_list, axis=0/1）：沿着指定axis进行数组的合并
np.vstack或者np.row_stack(array_list)：垂直vertically、按行row wise进行数据合并
np.hstack或者np.column_stack(array_list)：水平horizontally、按列column wise进行数据合并

按行合并

np.concatenate([a,b])

np.vstack([a,b])

np.row_stack([a, b])

按列合并

np.concatenate([a,b], axis=1)

np.hstack([a,b])

np.column_stack([a,b])

7.K折交叉验证

背景：K折交叉验证

为什么需要这个？
在机器学习中，因为如下原因，使用K折交叉验证能更好评估模型效果：

样本量不充足，划分了训练集和测试集后，训练数据更少；
训练集和测试集的不同划分，可能会导致不同的模型性能结果；

K折验证是什么
K折验证（K-fold validtion）将数据划分为大小相同的K个分区。
对每个分区i，在剩余的K-1个分区上训练模型，然后在分区i上评估模型。
最终分数等于K个分数的平均值，使用平均值来消除训练集和测试集的划分影响；

.............................................................................

用样本的角度解释下data数组：

这是一个二维矩阵，行代表每个样本，列代表每个特征
这里有9个样本，每个样本有4个特征

这是scikit-learn模型训练输入的标准格式

# 我们想进行4折交叉验证
k = 4

# 算出来每个fold的样本个数=2
k_samples_count = data.shape[0]//k

#range(k)=[0,1,2,3]
for fold in range(k):
validation_begin = k_samples_count*fold
validation_end = k_samples_count*(fold+1)
#取的是行data[validation_begin:validation_end]【0：2】【2：4】【4:6】【6:8】
validation_data = data[validation_begin:validation_end]

# np.vstack按行合并，沿着垂直的方向堆叠数组，validation_begin之前的数据和validation_end之后的数据进行合并
#[:0][2:] [:2][4:]
train_data = np.vstack([
data[:validation_begin],
data[validation_end:]
])

print()
print(f"#####第{fold}折#####")
print("验证集：\n", validation_data)
print("训练集：\n", train_data

#####第0折#####
验证集：[[0 1 2 3][4 5 6 7]]
训练集：[[ 8  9 10 11][12 13 14 15][16 17 18 19][20 21 22 23][24 25 26 27][28 29 30 31][32 33 34 35]]

#####第1折#####
验证集：[[ 8  9 10 11][12 13 14 15]]
训练集：[[ 0  1  2  3][ 4  5  6  7][16 17 18 19][20 21 22 23][24 25 26 27][28 29 30 31][32 33 34 35]]

#####第2折#####
验证集：[[16 17 18 19][20 21 22 23]]
训练集：[[ 0  1  2  3][ 4  5  6  7][ 8  9 10 11][12 13 14 15][24 25 26 27][28 29 30 31][32 33 34 35]]

#####第3折#####
验证集：[[24 25 26 27][28 29 30 31]]
训练集：[[ 0  1  2  3][ 4  5  6  7][ 8  9 10 11][12 13 14 15][16 17 18 19][20 21 22 23][32 33 34 35]]

8.numpy对数组排序

Numpy给数组排序的三个方法：

numpy.sort：返回排序后数组的拷贝
array.sort：原地排序数组而不是返回拷贝
numpy.argsort：间接排序，返回的是排序后的数字索引

3个方法都支持一个参数kind，可以是以下一个值：

quicksort：快速排序，平均O(nlogn)，不稳定情况
mergesort：归并排序，平均O(nlogn)，稳定排序
heapsort：堆排序，平均O(nlogn)，不稳定排序
stable：稳定排序

kind默认值是quicksort，快速排序平均情况是最快，保持默认即可

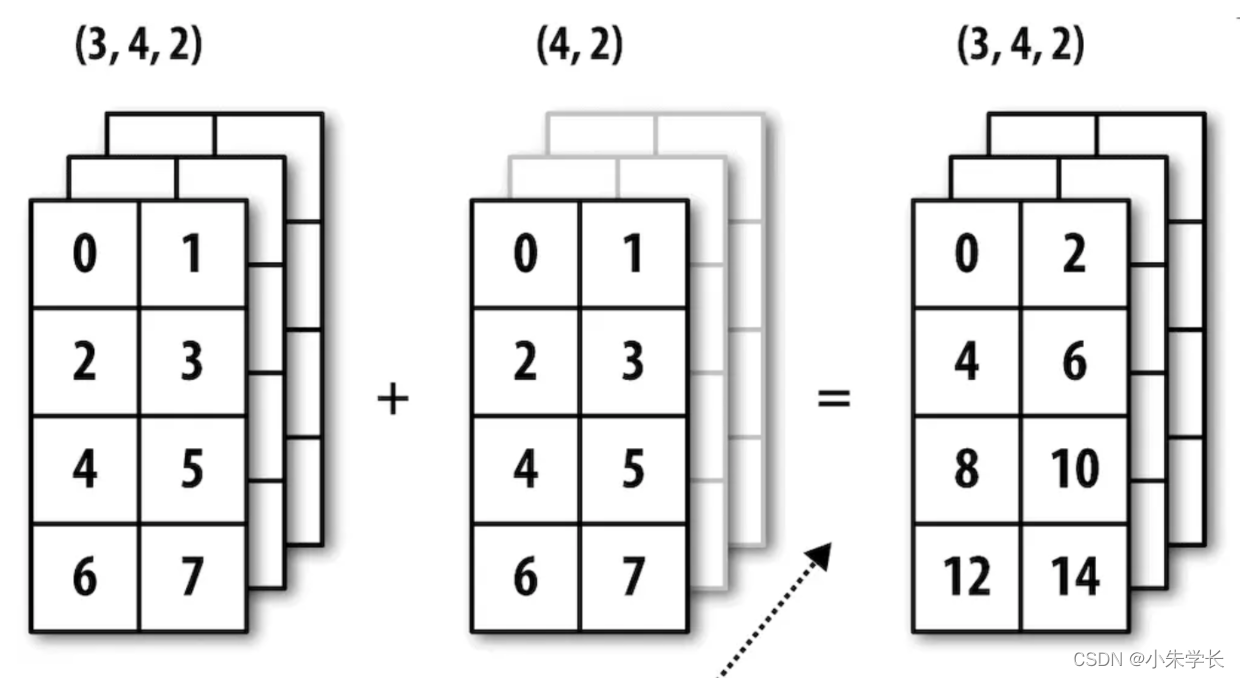
9.广播

广播：
简单理解为用于不同大小数组的二元通用函数（加、减、乘等）的一组规则

广播的规则：

如果两个数组的维度数dim不相同，那么小维度数组的形状将会在左边补1
如果shape的维度不匹配，但是有维度是1，那么可以扩展维度是1的维度匹配另一个数组；
如果shape的维度不匹配，但是没有任何一个维度是1，则匹配失败引发错误；

分析：a.shape=(2, 3), b.shape=(3,)

根据规则1，b.shape会变成(1, 3)
根据规则2，b.shape再变成(2, 3)，相当于在行上复制
完成匹配

扩展的是维度是1的(3, 2)变不成（3，3）

10.Numpy实现SVD矩阵分解

1 简介

SVD 全称：Singular Value Decomposition。SVD 是一种提取信息的强大工具，它提供了一种非常便捷的矩阵分解方式，能够发现数据中十分有意思的潜在模式。

主要应用领域包括：

隐性语义分析 (Latent Semantic Analysis, LSA) 或隐性语义索引 (Latent Semantic Indexing, LSI)；
推荐系统 (Recommender system)，可以说是最有价值的应用点；
矩阵形式数据（主要是图像数据）的压缩。

计算 MMH 和 MHM；
分别计算MMH和MHM的特征向量及其特征值；
MMH的特征向量组成U；而MHM的特征向量组成 V；
对MMH和MHM的非零特征值求平方根，对应上述特征向量的位置，填入Σ的对角元。

11.Numpy实现多项式曲线拟合

问题定义：
对于一堆数据点(x, y)，能否只根据这些数据，找出一个函数，使得函数画出来的曲线和原始数据曲线尽量匹配？

多项式拟合问题：
任何可微连续的函数，都可以用一个N次多项式来估计，而比N次幂更高阶的部分为无穷小可以忽略不计

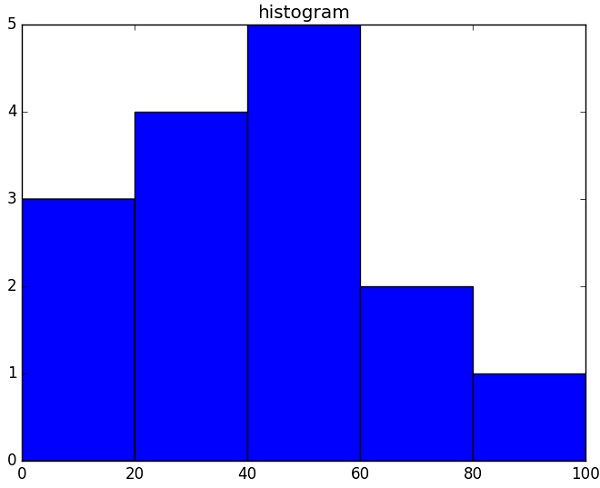
12.Numpy使用Matplotlib实现可视化绘图

13.Numpy数据输入给Sklearn实现模型训练

import numpy as np
# 使用sklearn自带的数据集，这些数据集都是Numpy的形式
# 我们自己的数据，也可以处理成这种格式，然后就可以输入给模型
from sklearn import datasets
# 用train_test_split可以拆分训练集和测试集
from sklearn.model_selection import train_test_split
# 使用LinearRegression训练线性回归模型
from sklearn.linear_model import LinearRegression

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。

13.1. 加载波斯顿房价数据集

# 加载数据集，存入特征矩阵data、预测结果向量target

#每个二维的数据集对应着一个一维的标签集，用于标识每个样本的所属类别或属性值。通常数据集用大写字母X表示，标签集用小写字母y表示。
data, target = datasets.load_boston(return_X_y=True)

参数:
return_X_y : 布尔值,默认为False,如果是True的话,返回(data, target)代替Bunch对象.

返回值:
Bunch对象.类似于字典的对象.其中的属性有:‘data’, the data to learn, ‘target’, the regression targets, and ‘DESCR’, the full description of the dataset.
或者是(data, target) :当return_X_y设为True的时候.