本文为视觉 SLAM 学习笔记，讲解视觉里程计中的特征点法。

本讲内容概要

• 图像特征的意义，在单幅及多幅图像中提取特征点。
• 对极几何的原理，利用对极几何的约束恢复图像间相机的三维运动
• PnP 问题，利用已知三维结构与图像的对应关系求解相机的三维运动
• ICP 问题，利用点云的匹配关系求解相机的三维运动
• 通过三角化获得二维图像上对应点的三维结构

特征点法

经典 SLAM 模型中以位姿——路标（Landmark）来描述 SLAM 过程。我们在经典 SLAM 系统中说的运动方程是位姿与位姿之间的关系，而观测方程说的是位姿与路标的关系。

路标是三维空间中固定不变的点，且需满足以下的特点：

• 数量充足，以实现良好的定位
• 较好的区分性，以实现数据关联

在视觉 SLAM 中，·通常利用图像特征点作为 SLAM 中的路标，称为特征法。

特征点

特征点是图像中比较有代表性的部分，例如下图中的角点、边缘、区块：

好的特征点需要满足以下几个特点：

• 可重复性：在不同地方观察同一特征点，相差不应该过大
• 可区分性：不同特征点应该易于辨别
• 高效：特征点的提取和匹配效率要高
• 本地：特征只与图像局部性质有关

我们很容易看出，区分性排序为：角点＞边缘＞区块。因此在视觉 SLAM 中，我们通常使用角点作为特征点，边缘在某些情况下会用到，区块一般不用。

特征点的信息

特征点自己的信息有位置、大小、方向、评分等，称为关键点。

我们一般不通过特征点本身来区分特征点，而是通过点周围的图像来区分，因为同一特征点可能因为光照等因素的变化亮度差很大，误被识别为不同特征点。特征点周围的图像信息被称为描述子。描述子随着相机角度或光照的变化而变化不大。

当我们要找到表现好的描述子，其计算量会变大。SIFT 具有平移、缩放和旋转的不变性，性能高但计算量很大。比如 ORB 描述子为简单描述子，只有平移或缩放（尺度）不变性，性能不高但计算量小，可以满足实时性。目前 ORB 描述子在 SLAM 中是一种很好的描述。

如果你对各种关键点和描述子感兴趣，建议参考 OpenCV features2d 模块。

ORB 特征

因为 ORB 是 SLAM 中较为成功的一种描述，我们以它为代表介绍特征。SIFT 的相关资料已经有很多介绍，可自行查阅。

ORB 的关键点是一个 Oriented FAST，即带旋转的 FAST ，其描述也是带旋转的 BRIEF。FAST 和 BRIEF 都是在特征描述中属于较为简单实时性好，但精度不好的方式，SLAM 中图像位移不大时也是可以匹配到的。

FAST 是一种关键点。其思想为：以一个点为中心，周围取像素，如果连续有 n 个点的灰度值与中心点相差一个阈值以上，我们就认为该点为关键点。这种方式计算量很小，只是比大小，因此提取 FAST 点速度很快，还可以使用一些加速手段。如取中心点周围 10 个点进行比较，则称为 FAST10。但是这样提取到 FAST 点太多，我们还需要网格等计算评分来筛选出好的特征点，然后特征点就可以使用了。

但是这样提出的 FAST 只是一个位置，我们还需要计算一个 FAST 旋转。旋转相当于图像的重心，如果左边为暗右边为亮则指向右边，最后计算得到的是图像梯度指向的角度。旋转的计算过程如下：

1. 在一个小的图像块 $B$ 中，定义图像块的矩为：

   m p q = ∑ x , y ∈ B x p y q I ( x , y ) , p , q = { 0 , 1 } m_{pq}=\sum\limits_{x,y∈B}x^py^qI(x,y),\quad p,q=\{0,1\} mpq​=x,y∈B∑​xpyqI(x,y),p,q={0,1}

2. 通过矩可以找到图像块的质心：
   $$C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})$$

3. 连接图像块的几何中心 $O$ 与质心 $C$，得到一个方向向量 $\overrightarrow{OC}$，于是特征点的方向可以定义为：
   $$\theta =arctan(m_{01}/m_{10})$$

FAST 只有平移不变性和旋转不变性，但没有尺度（缩放）不变性。尺度不变性为：当从远处和近处看向 FAST 是否还是角点，或者分辨率不同的情况下 FAST 角点还是不是角点。解决这个问题，我们一般会将图像做一个图像金字塔。最底层为图像最原始的分辨率，上面几层为原始图像缩小后的图像，最终构成一个分辨率不同大小的图像为金字塔。我们可以给每层提取一个 FAST，这样就获得了各种尺度下的 FAST 特征，我们可认为其具有一定程度上的尺度不变性。

BRIEF

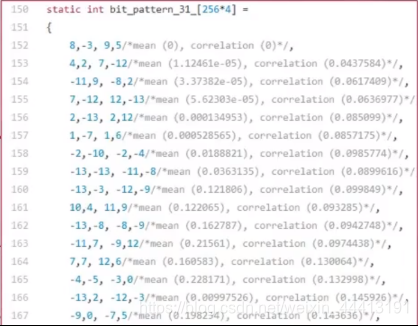
BRIEF 是一种二进制的描述子，如 BRIEF-128 为 128 位，每一位表示附近每个点对 A、B 的大小关系，使用汉明距离进行计算。BRIEF 描述了附近图像的信息，可作为 FAST 点的描述。A、B 点对的选取可随机均匀分布、满足高斯分布或满足特定 pattern。已有文献对不同的选取方式进行了测试，结果相差不大，我们可以随机选取。在选定某种固定的 pattern 后不能再变，否则失去了比较的意义。

在计算描述的时候，需要先将图像按照 FAST 中计算的角度进行旋转，再去进行比较，称为旋转后的 BRIEF。下图为 ORB-SLAM 的 pattern：

特征匹配

我们已经有了两张图的特征点，现在需要通过判断描述子的差异来判断哪些特征为同一个点。

最简单的特征匹配方法为暴力匹配，即 A 中一特征点与 B 中所有特征点之间计算描述子的距离，哪个最小就匹配哪个。描述子距离表示了两特征间的相似程度，可取不同的距离量度范数。对于浮点类型的描述子，使用欧氏距离，对于二进制的描述子（如 BRIEF），使用汉明距离。

当想要某帧和一张地图时，暴力匹配运算量过大，需要**快速近似最近邻（FLANN）**算法来加速。因为其过程较为复杂，且实现已经集成到 OpenCV，这里不进行介绍，如果感兴趣可自行百度。

实践：特征提取和匹配

OpenCV 的安装见 Ubuntu 安装 OpenCV。

首先读取两张图像，在这两张图像间进行特征匹配：

if ( argc != 3 )
{cout<<"usage: feature_extraction img1 img2"<<endl;return 1;
}
//-- 读取图像
Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );

然后申请关键点、描述子和匹配：

//-- 初始化
std::vector<KeyPoint> keypoints_1, keypoints_2;
Mat descriptors_1, descriptors_2;
Ptr<FeatureDetector> detector = ORB::create(); // 在这里可以设置提取特征点的数量
Ptr<DescriptorExtractor> descriptor = ORB::create();
// 不能使用欧氏距离，要声明汉明距离
Ptr<DescriptorMatcher> matcher  = DescriptorMatcher::create ( "BruteForce-Hamming" );

第一步：检测 Oriented FAST 角点位置

detector->detect ( img_1,keypoints_1 );
detector->detect ( img_2,keypoints_2 );

第二步：根据角点位置计算 BRIEF 描述子

descriptor->compute ( img_1, keypoints_1, descriptors_1 );
descriptor->compute ( img_2, keypoints_2, descriptors_2 );
Mat outimg1;
// 画出提取的特征
drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
imshow("ORB特征点",outimg1);

第三步：对两幅图像中的 BRIEF 描述子进行匹配，使用 Hamming 距离

vector<DMatch> matches;
//BFMatcher matcher ( NORM_HAMMING );
matcher->match ( descriptors_1, descriptors_2, matches );

第四步：匹配点对筛选。因为使用了暴力匹配，第一个图中的每个点不一定都在第二张图中有匹配，因此存在很多误匹配的点，要进行筛选。

double min_dist=10000, max_dist=0;//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for ( int i = 0; i < descriptors_1.rows; i++ )
{double dist = matches[i].distance;if ( dist < min_dist ) min_dist = dist;if ( dist > max_dist ) max_dist = dist;
}// 仅供娱乐的写法
min_dist = min_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance;
max_dist = max_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance;printf ( "-- Max dist : %f \n", max_dist );
printf ( "-- Min dist : %f \n", min_dist );//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
std::vector< DMatch > good_matches;
for ( int i = 0; i < descriptors_1.rows; i++ )
{if ( matches[i].distance <= max ( 2*min_dist, 30.0 ) ){good_matches.push_back ( matches[i] );}
}

第五步：绘制匹配结果

Mat img_match;
Mat img_goodmatch;
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
imshow ( "所有匹配点对", img_match );
imshow ( "优化后匹配点对", img_goodmatch );
waitKey(0);

如果此时发生报错：

pose_estimation_3d2d.cpp:151:50: error: no matching function for call to ‘g2o::BlockSolver<g2o::BlockSolverTraits<6, 3> >::BlockSolver(g2o::BlockSolver<g2o::BlockSolverTraits<6, 3> >::LinearSolverType*&)’Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器^
In file included from /usr/local/include/g2o/core/block_solver.h:199:0,from /home/xin/Slam/slambook/slambook-master/ch7/pose_estimation_3d2d.cpp:10:

出现这种错误的原因是 g2o 的新旧版本间指针类型不匹配。我们需要进行修改。

在 pose_estimation_3d2d.cpp 中，第 151-152 行，修改前代码如下：

Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );

修改后代码（修改的是 151-152 行）：

Block* solver_ptr = new Block ( std::unique_ptr<Block::LinearSolverType>(linearSolver) );     // 矩阵块求解器
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::unique_ptr<Block>(solver_ptr) );

在 pose_estimation_3d3d.cpp 中，第 279-280 行，修改前代码如下：

Block* solver_ptr = new Block( linearSolver );      // 矩阵块求解器
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );

修改后代码：

Block* solver_ptr = new Block( std::unique_ptr<Block::LinearSolverType>(linearSolver) ); // 矩阵块求解器
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( std::unique_ptr<Block>(solver_ptr) );

最后在 1.png, 2.png 下执行：

./build/feature_extraction 1.png 2.png

提取的特征点如下图，可见特征点都集中在灰度变化明显的地方：

暴力匹配得到的匹配结果，存在大量误匹配：

经过筛选之后，剩下的匹配大多都是正确的匹配：

特征点匹配后，得到了特征点之间的关系：

• 若只有两个单目图像，得到 2D-2D 间的关系——对极约束
• 若匹配的是帧和地图，得到 3D-2D 间的关系——PnP
• 若匹配的是 RGB-D 图，得到 3D-3D 间的关系——ICP

2D-2D：对极几何

对极约束

现在，我们以及找到了很对匹配的点，下面为其中的一个点对：

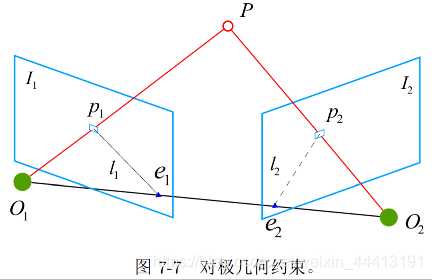
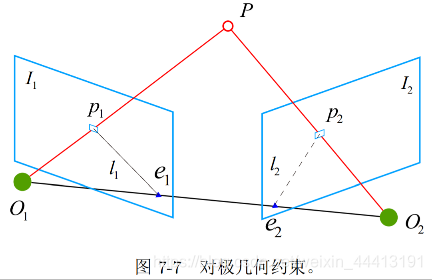
几何关系：

• 两个相机中心分别为 $O_1,O_2$，$P$ 在两个图像的投影为 $p_1,p_2$，连线 $\overrightarrow{O_1{p}_1},\overrightarrow{O_2{p}_2}$ 在三维空间中相交于点 $P$，为路标点

• $l_1$ 为 $\overrightarrow{O_2{p}_2}$ 在平面 $I_1$ 的投影，称为极线，$e_1,e_2$ 称为极点

• 两个相机之间的变换为 $T_{12}$

实践中：

• $p_1,p_2$ 通过特征匹配得到，$P$ 未知，$e_1,e_2$ 未知，$T_{12}$ 待求。
• 这是一个通过匹配点建图和求解位姿的问题，是经典的 SLAM 问题

我们设世界坐标为 $P=[X,Y,Z{]}^T$。由相机模型，两个像素点 $p_1,p_2$ 的像素位置为：
$$s_1{p}_1=KP,s_2{p}_2=K(RP+t)$$
使用归一化坐标（去掉内参）：
$$x_1=K^{-1}{p}_1,x_2=K^{-1}{p}_2$$
$x_1,x_2$ 是两个像素点的归一化平面上的坐标，带入上式得齐次关系：
$$x_2=R{x}_1+t$$
两侧左乘 $\hat{t}$，相当于两边同时与 $t$ 叉乘：
$$\hat{t}{x}_2=\hat{t}R{x}_1$$
两边左乘 $x_2^T$：
$$x_2^T\hat{t}{x}_2=x_2^T\hat{t}R{x}_1$$
因为 $\hat{t}{x}_2$ 是一个与 $t$ 和 $x_2$ 都垂直的向量，与 $x_2$ 做内积时为 0：
$$x_2^T\hat{t}R{x}_1=0$$
重新代入 $p_1,p_2$：
$$p_2^T{K}^{-T}\hat{t}R{K}^{-1}{p}_1=0$$
上面两个式子为对极约束。

设本质矩阵 $E=\hat{t}R$，基础矩阵 $F=K^{-T}E{K}^{-1}$，上式化简为：
$$x_2^{T}E{x}_1=p_2^{T}F{p}_1=0$$
在 SLAM 中内参 $K$ 已知，可以使用 $E$。

尺度不确定性

在前面 $x_2^T\hat{t}R{x}_1=0$ 中，给 $R$ 数乘后等式仍成立，则 $E=\hat{t}R$ 有多解，为尺度不确定性。

位姿估计的步骤

1. 根据匹配点对的像素位置求出 $E$
2. 由 $E$ 恢复 $R,t$

对极约束性质：

• 乘任意非零常数，对极约束仍满足，$E$ 在不同尺度下等价
• 平移和旋转共 3 个自由度，$\hat{t}R$ 共 6 个自由度，由于尺度不变性会丢失一个自由度，故 $E$ 只有 5 个自由度。但 $E$ 的非线性性质会使 5 对点求解困难
• 将 $E$ 当作普通矩阵用 8 点法估计 $E$，只利用了 $E$ 的线性性质。

本质矩阵——八点法求 $E$

考虑一对匹配点的对极约束：

将 $E$ 展开为向量形式：
$$\vec{e}=[e_1,e_2,e_3,e_4,e_5,e_6,e_7,e_8,e_9{]}^T$$
对极约束可以写为线性形式：
$$[u_1{u}_1,u_1{v}_2,u_1,v_1{u}_2,v_1{v}_2,v_1,u_2,v_2,1]\cdot \vec{e}=0$$
将 8 对点放入方程中，得到线性方程组：

$ax=0$，解出 $x$ 得到 $E$ 即可。方程的解是欠定的，$ke$ 也是方程的解。这与 $e$ 的尺度等价性是一致的。

从 $E$ 计算 $R,t$：奇异值（SVD）分解：
$$E=U\Sigma V^T$$

$$\widehat{t_1}=U{R}_Z(\frac{\pi }{2})\Sigma U^T,R_1=U{R}_Z^T(\frac{\pi }{2})V^T$$

$$\widehat{t_2}=U{R}_Z(-\frac{\pi }{2}\Sigma U^T),R_2=U{R}_Z^T(-\frac{\pi }{2})V^T$$

得到四组解：

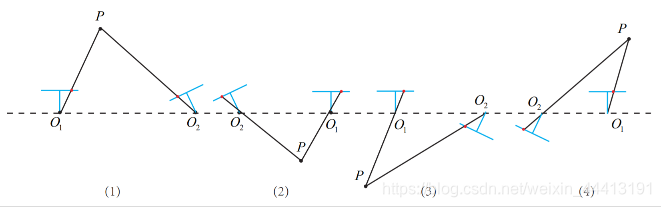
将验证点带入解中，只有 1 个为正，即为正确解。

讨论八点法

1. 用于单目初始化。相机运动过程中地图为 3D 的，可以使用 PnP 求解，因此八点法只在初始化时使用
2. 尺度不确定性：将轨迹和地图缩放任意倍，得到观测值相同。因此在实际中，我们将 $t$ 归一化或将特征点的平均深度设为 1。即要么限制运动，要么限制结构，否则会任意倍的放缩
3. 纯旋转时，即 $t=0$ 时，$E=0$ 无法分解
4. 因为两张图有很多特征点，当多于 8 对时，我们计算最小二乘法或 RANSAC（后面会详细讲解）。

单应矩阵

从单应矩阵恢复 $R,t$ 时，八点法在特征点共面时会退化。设特征点位于某平面上：$n^{T}P+d=0$ 或 $-\frac{n^{T}P}{d}=1$。则两个图像特征点的坐标关系为：
$$p_2=K(RP+t)=\dots =K(R-\frac{t{n}^T}{d})K^{-1}{p}_1$$
我们得到了直接描述图像坐标 $p_1$ 和 $p_2$ 间的变换。将中间的部分记为 $H$：
$$p_2=H{p}_1$$
展开后有：

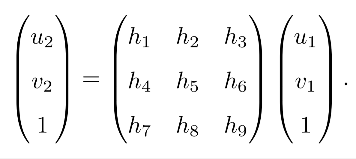
写成关于 $H$ 的线性方程：

类似八点法，先计算 $H$，再用 $H$ 恢复 $R,t,n,d,K$。

小结

在 2D-2D 情况下，只知道图像坐标之间的对应关系。

• 当特征点在平面上时（例如俯视和仰视），使用 $H$ 恢复 $R,t$
• 否则使用 $E$ 或 $F$ 恢复 $R,t$

求得 $R,t$ 后，利用三角化计算特征点的 3D 位置，即深度。

实践：对极约束求解相机运动

首先是特征点匹配封装为一个函数，具体内容与前面实践相同：

void find_feature_matches (const Mat& img_1, const Mat& img_2,std::vector<KeyPoint>& keypoints_1,std::vector<KeyPoint>& keypoints_2,std::vector< DMatch >& matches );

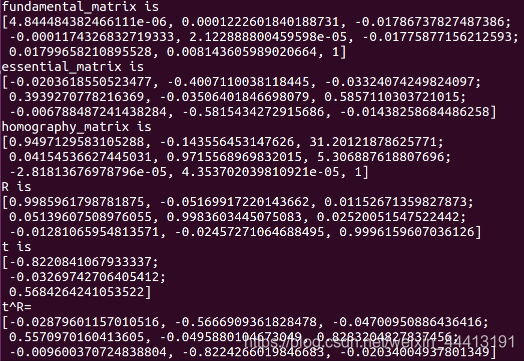
然后计算基础矩阵、本质矩阵和单应矩阵，并恢复相机位姿 $R_{21},t_{21}$：

//-- 计算基础矩阵
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
cout<<"fundamental_matrix is "<<endl<< fundamental_matrix<<endl;//-- 计算本质矩阵
Point2d principal_point ( 325.1, 249.7 );	//相机光心, TUM dataset标定值
double focal_length = 521;			//相机焦距, TUM dataset标定值
Mat essential_matrix;
essential_matrix = findEssentialMat ( points1, points2, focal_length, principal_point );
cout<<"essential_matrix is "<<endl<< essential_matrix<<endl;//-- 计算单应矩阵
Mat homography_matrix;
homography_matrix = findHomography ( points1, points2, RANSAC, 3 );
cout<<"homography_matrix is "<<endl<<homography_matrix<<endl;//-- 从本质矩阵中恢复旋转和平移信息.
recoverPose ( essential_matrix, points1, points2, R, t, focal_length, principal_point );
cout<<"R is "<<endl<<R<<endl;
cout<<"t is "<<endl<<t<<endl;

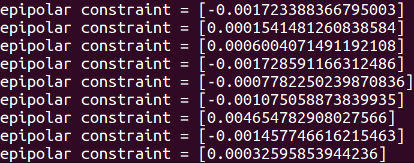
然后还可以对其进行验证，验证对极约束是否近似为 0：

Mat K = ( Mat_<double> ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
for ( DMatch m: matches )
{Point2d pt1 = pixel2cam ( keypoints_1[ m.queryIdx ].pt, K );Mat y1 = ( Mat_<double> ( 3,1 ) << pt1.x, pt1.y, 1 );Point2d pt2 = pixel2cam ( keypoints_2[ m.trainIdx ].pt, K );Mat y2 = ( Mat_<double> ( 3,1 ) << pt2.x, pt2.y, 1 );Mat d = y2.t() * t_x * R * y1;cout << "epipolar constraint = " << d << endl;
}

得到的矩阵输出结果如下，其中 $E$ 与 $\hat{t}R$ 只差一个倍数：

验证对极约束，因为误差的存在，得到的结果近似为 0：

OpenCV 中仅使用了 $E$ 来求解 $R,t$，关于如何使用 $H$ 求解位姿没有直接提供，可以参考 ORB-SLAM 和 SVO。

三角测量

前面已经求解出了运动，现在要根据运动求解特征点的 3D 位置。几何关系为：
$$s_1{x}_1=s_{2}R{x}_2+t$$
求 $s_2$ 时，两侧乘 $\widehat{x_1}$：
$$s_1\widehat{x_1}{x}_1=0=s_2\widehat{x_1}R{x}_2+\widehat{x_1}t$$
反之亦然。

或者同时解 $s_1,s_2$，求 $[-R{x}_2,x_1]\left[\begin{array}{c}{s}_1\\ s_2\end{array}\right]=t$ 的最小二乘解：
$$x=(A^{T}A{)}^{-1}{A}^{T}b$$
系数矩阵的伪逆不可靠，$A^{T}A$ 行列式近似 0。

解得深度的质量与平移相关，但平移大时特征匹配可能不成功。相机前进时虽然有位移，但位于图像中心的点无法三角化（没有视差）。

实践：三角测量

直接调用 OpenCV 中的接口，传入 2D 位姿，得到齐次坐标：

Mat pts_4d;
cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );

3D-2D：PnP

已知 3D 点的空间位置（世界坐标）和相机上的投影点，求解相机的旋转和平移（外参）。有两种方法：

• 代数：构造线性方程问题，用线性代数方法求解。不鲁棒。方法有 DLT、P3P 等。
• 优化：构建优化问题，通常定义误差，最小化误差。有初始值时通常选择优化方法。方法有 Bundle Adjustment

直接线性变换（DLT）

设空间点 $P=(X,Y,Z{)}^T$，其投影点位 $x=(u,v,1)$，用归一化坐标表示。投影关系为 $sx=[R|t]p$，这里 $[R|t]$ 为增广矩阵，展开后有：

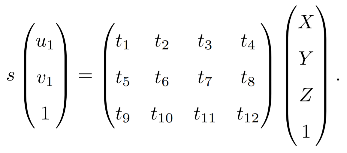
其中 $x,p$ 已知。将其看成关于 $t$ 的线性方程，求解 $t$。注意最下面的一行：
$$s=[t_9,t_{10},t_{11},t_{12}][X,Y,Z,1{]}^T$$
用它消去前两行的 $s$，则一对特征点可以提供 2 个方程：
$$t_1^{T}P-t_3^{T}P{u}_1=0,t_2^{T}P-t_3^{T}P{v}_1=0$$
因此，为了求解 12 个未知数，需要 $12/6=6$ 对点。如果超出 6 对，求解最小二乘解。

我们在 DLT 时将 $R,t$ 看作了独立的未知量，因此求解后的结果可能不满足旋转矩阵的约束，因此我们还需要使用 QR 分解将矩阵投影回 $SO(3)$。

P3P

利用 3 对点求相机外参。

对应关系：
$$\Delta Oab-\Delta OAB,\Delta Obc-\Delta OBC,\Delta Oac-\Delta OAC$$
由余弦定理有：
$$O{A}^2+O{B}^2-2OA\cdot OB\cdot cos<a,b>=A{B}^2$$

$$O{B}^2+O{C}^2-2OB\cdot OC\cdot cos<b,c>=B{C}^2$$

$$O{A}^2+O{C}^2-2OA\cdot OC\cdot cos<a,c>=A{C}^2$$

对上面 3 个式子同时除以 $O{C}^2$，并记 $x=OA/OC,y=OB/OC$ 得：
$$x^2+y^2-2xycos<a,b>=A{B}^2/O{C}^2$$

$$y^2+1-2ycos<b,c>=B{C}^2/O{C}^2$$

$$x^2+1-2xcos<a,c>=A{C}^2/O{C}^2$$

记 $v=A{B}^2/O{C}^2,uv=B{C}^2/O{C}^2,wv=A{C}^2/O{C}^2$，有：
$$x^2+y^2-2xycos<a,b>-v=0$$

$$y^2+1-2ycos<b,c>-uv=0$$

$$x^2+1-2xcos<a,c>-wv=0$$

用第一个式子代入下面两个消去 $v$，得到关于 $x,y$ 的二元二次方程，用吴氏消元法解析解得：
$$(1-u)y^2-u{x}^2-cos<b,c>+2uxycos<a,b>+1=0$$

$$(1-w)x^2-w{y}^2-cos<a,c>x+2wxycos<a,b>+1=0$$

得到 $x,y$ 后，利用：
$$x^2+y^2-2xycos<a,b>=v$$
解得 $v$，从而得到 $OC$ 的长度，进而得到各点的距离。

但是 P3P 对三个点以上的情况难以处理，并且误匹配时算法会失效。

Bundle Adjustment

Bundle Adjustment 是一个最小重投影误差问题，下面给出两个视图间的形式。

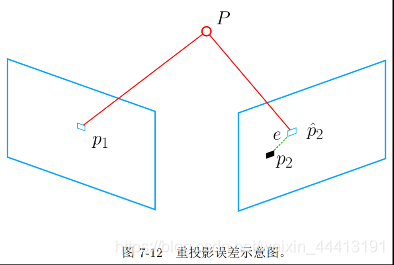
$p_2$ 为 $P$ 的真实投影点，但因为相机位姿估计上的误差，投影点会变为 $\widehat{p_2}$，因此我们需要最小化重投影的误差来优化相机位姿。

在第六讲我们讲过非线性优化，因此这里只需要定义一个最小二乘问题，并将 $J$ 推导出来即可。

投影关系：
$$s_i{u}_i=K\exp (\hat{\xi })P_i$$
因为外参是估计的，因此等式存在误差。定义重投影误差并对其二范数的平方和取最小化：
$${\xi }^{\ast }=\arg \underset{\xi }{\min }\frac{1}{2}\sum _{i=1}^n||u_i-\frac{1}{s_i}K\exp (\hat{\xi })P_i|{|}_2^2$$
因为我们需要知道误差对应着的位姿，需要利用扰动模型求误差相对于位姿的导数。最后用非线性优化的知识进行求解即可，中间推导过程有些复杂，限于篇幅不做介绍。

实践：求解 PnP

首先使用前面介绍的特征匹配找到 ORB 特征，然后计算相机位姿，调用了 OpenCV 的 solvePnP 函数

// 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
// 给定2d和世界坐标3d点和内参，返回R、t
solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false );

也可以用 Bundle Adjustment 解决 PnP 问题，使用 g2o 优化，选好顶点和边即可。顶点为用李代数表示的相机位姿（VertexSE3Expmap），误差定义为 $X,Y,Z$ 投影到 $u,v$ 的投影误差（VertexSBAPointXYZ）。本实验中使用的是 g2o 自带的 edge，没有必要把雅可比再实现一遍。但以后在实际当中如果自己定义了 edge，就要计算导数。

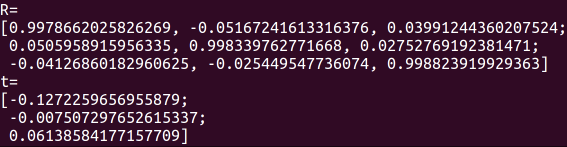
EPnP 计算得到的结果：

然后是用 Bundle Adjustment 优化得到的结果：

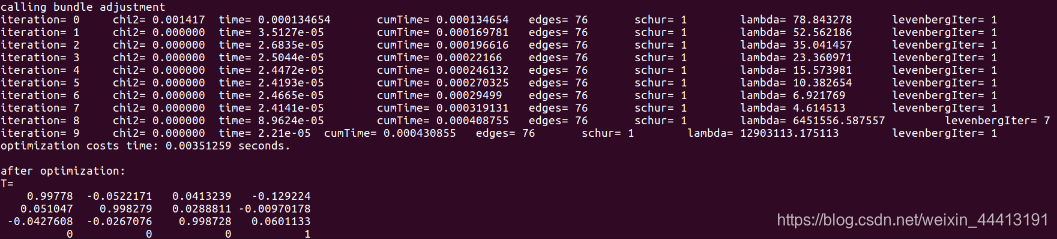
一开始误差较大，随着迭代次数的增加，误差 $\xi$ 逐渐减小。优化后的位姿与优化前相差不大，但更加平滑。

3D-3D：ICP

给定匹配好的两组 3D 点，求其旋转和平移，可用迭代最近邻点（ICP）求解。

设 P = { p 1 , … , p n } , P ′ = { p 1 ′ , … , p n ′ } P=\{p_1,…,p_n\}, \quad P'=\{p_1',…,p_n'\} P={p1​,…,pn​},P′={p1′​,…,pn′​}，运动关系为 $p_i=R{p}_i^{\prime }+t$。

我们有两种方法求解这个问题。

SVD 方法

定义误差项 $e_i=p_i-(R{p}_i^{\prime }+t)$，以及最小二乘问题：
$$\underset{R,t}{\min }J=\frac{1}{2}\sum _{i=1}^n||(p_i-(R{p}_i^{\prime }+t))|{|}_2^2$$
稍加推导，定义质心 $p=\frac{1}{n}\sum _{i=1}^n(p_i),p^{\prime }=\frac{1}{n}\sum _{i=1}^n(p_i^{\prime })$，改写目标函数：
$$\frac{1}{2}\sum _{i=1}^n||(p_i-(R{p}_i^{\prime }+t))|{|}_2^2=\frac{1}{2}\sum _{i=1}^n||(p_i-R{p}_i^{\prime }-t-p+R{p}^{\prime }+p-R{p}^{\prime })|{|}^2$$

$$=\frac{1}{2}\sum _{i=1}^n||(p_i-p-R(p_i^{\prime }-p^{\prime }))+(p-R{p}^{\prime }-t)|{|}^2$$

展开后：
$$=\frac{1}{2}\sum _{i=1}^n(||p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2+||p-R{p}^{\prime }-t|{|}^2+2(\dots ))$$
其中交叉项求和为 0。目标函数简化为：
$$\underset{R,t}{\min }J=\frac{1}{2}\sum _{i=1}^n(||p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2+||p-R{p}^{\prime }-t|{|}^2$$
其中第一项只和 $R$ 有关，第二项和 $R,t$ 有关，我们可以最小化第一项，然后令第二项为 0 得到 $t$。

现在对左侧的式子（旋转）进行求解。

定义去质心坐标 $q_i=p_i-p,q_i=p_i^{\prime }-p^{\prime }$，简化为：
$$R^{\ast }=\arg \underset{R}{\min }\frac{1}{2}\sum _{i=1}^n||q_i-R{q}_i^{\prime }|{|}^2$$
展开后：
$$=\frac{1}{2}\sum _{i=1}^n{q}_i^T{q}_i+q_i^{\prime T}{R}^{T}R{q}_i^{\prime }-2q_i^{T}R{q}_i^{\prime }$$
其中第一项与 $R$ 无关，第二项 $R^{T}R$ 的结果为 $I$，因此只需要最小化最后一项：
$$\sum _{i=1}^n-q_i^{T}R{q}_i^{\prime }=\sum _{i=1}^n-tr(R{q}_i^{\prime }{q}_i^T)=-tr(R\sum _{i=1}^n{q}_i^{\prime }{q}_i^T)$$
利用 SVD 可以解出结果：
$$W=\sum _{i=1}^n{q}_i{q}_i^T,W=U\Sigma V^T,R=U{V}^T$$

非线性优化

已知匹配时，ICP 问题存在唯一解或无穷多解。唯一解时问题为凸问题，极小值就是全局最优解，初始值可以随意指定。非线性优化的结果与 SVD 一样，且优化很快收敛。

在激光情况下，可能未知匹配关系，我们认为距离最近的两个点为同一个，所以该方法称为迭代最近点。

由于一个像素的深度数据可能测量不到，我们可以混用 PnP 和 ICP 优化，将所有误差放在同一个问题中考虑，方便求解。

实践：求解 ICP

这里演示两种求解 ICP 的方法。

SVD 方法

只需要根据我们刚才的推导过程写出代码即可。首先计算质心：

Point3f p1, p2;
int N = pts1.size();
for ( int i=0; i<N; i++ )
{p1 += pts1[i];p2 += pts2[i];
}
p1 = Point3f( Vec3f(p1) /  N);
p2 = Point3f( Vec3f(p2) / N);

然后去质心：

vector<Point3f>     q1 ( N ), q2 ( N );
for ( int i=0; i<N; i++ )
{q1[i] = pts1[i] - p1;q2[i] = pts2[i] - p2;
}

计算 $W$：

// compute q1*q2^T
Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for ( int i=0; i<N; i++ ){W += Eigen::Vector3d ( q1[i].x, q1[i].y, q1[i].z ) * Eigen::Vector3d ( q2[i].x, q2[i].y, q2[i].z ).transpose();
}
cout<<"W="<<W<<endl;

对 $W$ 进行 SVD 分解，求出 $U,V$：

Eigen::JacobiSVD<Eigen::Matrix3d> svd ( W, Eigen::ComputeFullU|Eigen::ComputeFullV );
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();if (U.determinant() * V.determinant() < 0)for (int x = 0; x < 3; ++x)U(x, 2) *= -1;
cout<<"U="<<U<<endl;
cout<<"V="<<V<<endl;

最后求解 $R,t$，转换为 cv::Mat：

Eigen::Matrix3d R_ = U* ( V.transpose() );
Eigen::Vector3d t_ = Eigen::Vector3d ( p1.x, p1.y, p1.z ) - R_ * Eigen::Vector3d ( p2.x, p2.y, p2.z );// convert to cv::Mat
R = ( Mat_<double> ( 3,3 ) <<R_ ( 0,0 ), R_ ( 0,1 ), R_ ( 0,2 ),R_ ( 1,0 ), R_ ( 1,1 ), R_ ( 1,2 ),R_ ( 2,0 ), R_ ( 2,1 ), R_ ( 2,2 ));
t = ( Mat_<double> ( 3,1 ) << t_ ( 0,0 ), t_ ( 1,0 ), t_ ( 2,0 ) );

非线性优化方法

edge 为单元边，只关联一个相机位姿，给定两个点，计算误差：

virtual void computeError(){const g2o::VertexSE3Expmap* pose = static_cast<const g2o::VertexSE3Expmap*> ( _vertices[0] );// measurement is p, point is p'_error = _measurement - pose->estimate().map( _point );
}

观测量关于位姿的导数（雅可比矩阵）：

_jacobianOplusXi(0,0) = 0;
_jacobianOplusXi(0,1) = -z;
_jacobianOplusXi(0,2) = y;
_jacobianOplusXi(0,3) = -1;
_jacobianOplusXi(0,4) = 0;
_jacobianOplusXi(0,5) = 0;_jacobianOplusXi(1,0) = z;
_jacobianOplusXi(1,1) = 0;
_jacobianOplusXi(1,2) = -x;
_jacobianOplusXi(1,3) = 0;
_jacobianOplusXi(1,4) = -1;
_jacobianOplusXi(1,5) = 0;_jacobianOplusXi(2,0) = -y;
_jacobianOplusXi(2,1) = x;
_jacobianOplusXi(2,2) = 0;
_jacobianOplusXi(2,3) = 0;
_jacobianOplusXi(2,4) = 0;
_jacobianOplusXi(2,5) = -1;

在 mian 中先找匹配，分别用 ICP 和 Bundle Adjustment 计算位姿：

Mat R, t;
pose_estimation_3d3d ( pts1, pts2, R, t );
cout<<"ICP via SVD results: "<<endl;
cout<<"R = "<<R<<endl;
cout<<"t = "<<t<<endl;
cout<<"R_inv = "<<R.t() <<endl;
cout<<"t_inv = "<<-R.t() *t<<endl;cout<<"calling bundle adjustment"<<endl;bundleAdjustment( pts1, pts2, R, t );

在 mian 中先找匹配，分别用 ICP 和 Bundle Adjustment 计算位姿：

Mat R, t;
pose_estimation_3d3d ( pts1, pts2, R, t );
cout<<"ICP via SVD results: "<<endl;
cout<<"R = "<<R<<endl;
cout<<"t = "<<t<<endl;
cout<<"R_inv = "<<R.t() <<endl;
cout<<"t_inv = "<<-R.t() *t<<endl;cout<<"calling bundle adjustment"<<endl;bundleAdjustment( pts1, pts2, R, t );