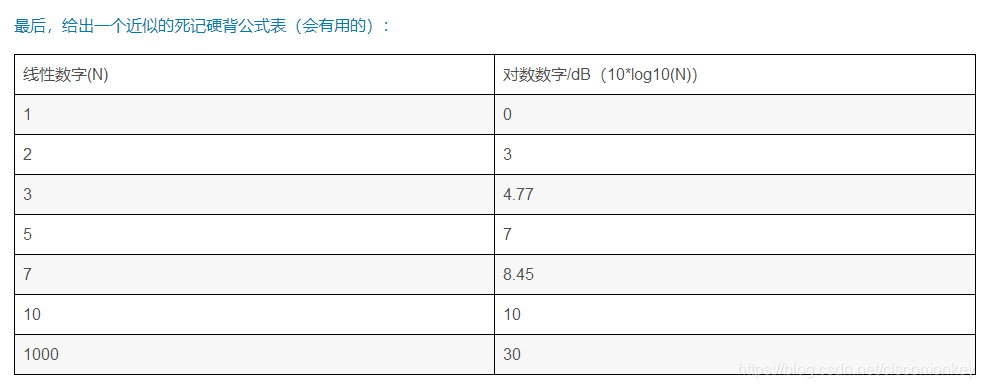
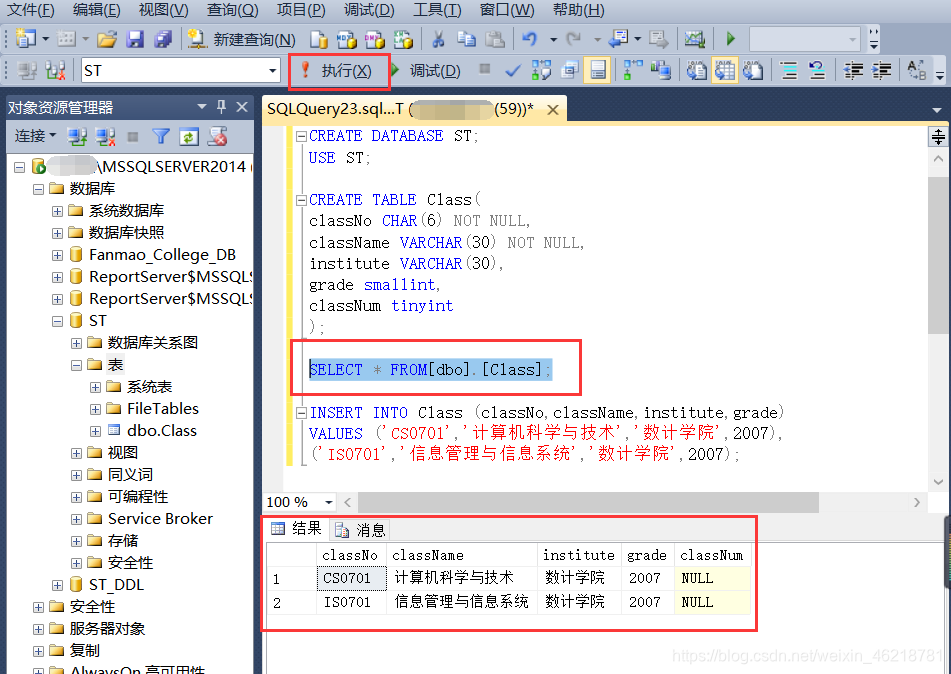
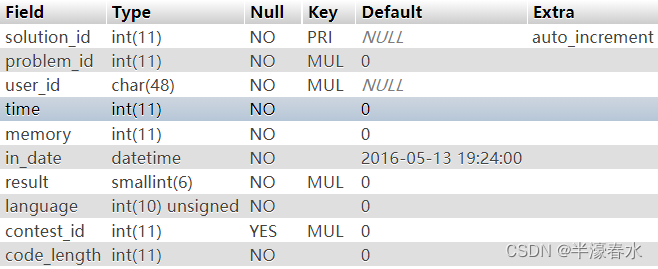
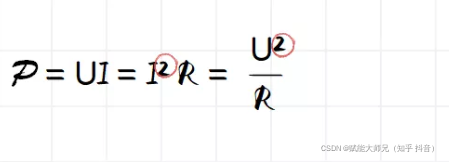图像分割 - 水平集算法

article/2024/12/26 20:11:40

水平集介绍

水平集分为三种：

1 . 基于图像边缘灰度梯度信息 ，适用于边缘强的图像分割

2 . 基于区域特征 ，利用区域信息引导曲线慢慢靠近，比如分割曲线区域的内外灰度均值，分割曲线内部区域面积（例如 Chan-Vase）

3 . 混合型

水平集关键：曲线的演变

首先设置一个初始轮廓，也就是初始轮廓，通过将这个初始轮廓演变成图像中需要分割出来的形状，那具体是如何演变的呢？我用自己的理解来解释一下：

既然曲线在演变，那曲线的每一个点一定有一个演化的方向，如何确定演化方向？

用最优方向，也就是梯度方向的法线方向，因为曲线沿这个方向变化最快 .

既然曲线在演变，每一个点不但有了方向也应该有一个速度，如何控制曲线演变速度呢？

用梯度信息，也就是图像的灰度分别对坐标轴两方向求偏导，靠近边缘变化慢，远离边缘变化快 .

Chan-Vese(CV) 算法

要用水平集实现图像分割， Chan-Vese算法是一个非常重要的算法，CV模型使用图像的像素灰度信息作为能量，构造能量函数，通过控制曲线内外图像的灰度值来实现曲线的演变，公式如下：

$Ec = \iint_{}^{} \left | I(x,y)-c1 \right |^2dxdy + \iint_{}^{} \left | I(x,y)-c2 \right |^2dxdy$

其中 $I(x,y)$ 表示原图像在 $(x,y)$ 坐标下的灰度值， $c1$ $c2$ 分别为曲线内外图像灰度值的均值 .

当曲线演变至目标轮廓时， $Ec$ 取极小值，内外能量守恒 .

$\iint_{}^{} \left | I(x,y)-c1 \right |^2dxdy \approx 0$

$\iint_{}^{} \left | I(x,y)-c2 \right |^2dxdy\approx 0$

再在 $Ec$ 上加上一些正则项，得出一个能量泛函：

$E = \mu Length(C)+\nu Area(C) +Ec$

引入水平集函数 : $\o \varnothing (x,y)$

先来说一下我对这个函数 $\varnothing (x,y)$ 的理解，我把它理解成一个描绘等高线的函数，他不是一个曲线函数，我们可以把它理解成一个面函数，从初始曲线映射的面函数，假设引入时间变量 $t$ ，随着时间 $t$ 在变曲线也就在演变，而面也就一层一层的向下演变，这个在之后的变分方程（E-L公式的介绍里会详细的说明）当演化到一定程度，再通过绘制等高线的方法，来实现图像最终的分割.

刚才既然说到水平集函数是一个面函数，那么如何表示曲线呢？这里就要引入Heaviside Fucntion(阶跃函数) 公式如下：

$\large H(z)=\left\{\begin{matrix} 1, &if &z>0 \\ 0,& if& z<0 \end{matrix}\right.$

这里阶跃函数的参数 $\large z$ 就是水平集函数 $\o (x,y)$

一般一个初始的轮廓设置时，变量是一个和原图相同大小的矩阵，轮廓内的值 $\o (x,y)$ 为 1，而轮廓外的值 $\o (x,y)$ 为 -1，通过慢慢演变， $\o (x,y)$

中的 -1逐渐增大变为正数，迭代到一定程度是，将轮廓曲线分割完成，而 $H(z)$ 阶跃函数的意义就是如果 $z$ ，也就是 $\o (x,y)$ 的值 $>0$ 了，说明该点已经被认为是演化出来的新的轮廓了.

能量泛函的定义

上面已经提到过，能量泛函为：

$E = \mu Length(C)+\nu Area(C) +Ec$

其中：

$Length(\o =0)=\iint_{}^{} \left | \bigtriangledown H(\o (x,y) \right |dxdy$

$Length(\o \geqslant 0)=\iint_{}^{} H(\o (x,y)dxdy$

$Ec = \iint_{}^{} \left | I(x,y)-c1 \right |^2H(\o )dxdy + \iint_{}^{} \left | I(x,y)-c2 \right |^2(1-H(\o ))dxdy$

并且每一个前面都需要有一个权重参数，所以总能量泛函就可以是：

$E=\mu \iint_{}^{} \left | \bigtriangledown H(\o (x,y) \right |dxdy+\nu \iint_{}^{} H(\o (x,y)dxdy+ \lambda 1\iint_{}^{} \left | I(x,y)-c1 \right |^2H(\o )dxdy + \lambda 2\iint_{}^{} \left | I(x,y)-c2 \right |^2(1-H(\o ))dxdy$

其中：

$c1 = \frac{\iint_{}^{}I(x,y)H(\o (x,y)dxdy}{\iint_{}^{}H(\o (x,y)dxdy}$

$c2= \frac{\iint_{}^{}I(x,y)(1-H(\o (x,y))dxdy}{\iint_{}^{}1-H(\o (x,y)dxdy}$

在理论上来讲，Heaviside Fucntion(阶跃函数)是不存在的，所以我们选择了一个替代函数（ $\epsilon$ 为常数）：

$H(z) = \frac{1}{2}(1+\frac{2}{\pi }arctan\frac{z}{\epsilon })$

为什么选择这个函数呢？因为后面变分法梯度下降的时候，会涉及到 $H(z)$ 求导，而数学好的已经发现了 $H(z)$ 求导是一个跟 $\epsilon$ 有关的常数 .

$\delta (z) =\frac{1}{\pi }*\frac{\epsilon }{\epsilon ^{2}+\pi ^{2}}$

当ϵ 的取值越小，替代函数也就越接近理想中的的阶跃函数。

求解能量泛函极值

我们使用变分法（欧拉 - 拉格朗日）和梯度下降来求泛函 $E$ 的最优解，公式如下：

$\frac{\partial \o }{\partial t} =\delta (\phi )[ \mu div(\frac{\bigtriangledown u}{\left | \bigtriangledown u \right |})-\upsilon - \lambda1(I-c1) ^{2}+\lambda 2(I-c2)^{2}]$