【MATLAB】三维旋转的实现

在这里插入图片描述

1 三维旋转的表达方式

三维空间中常用的表示旋转的方式有：

**[1]旋转矩阵(rotation matrix)
[2]旋转向量(rotation vector）/角轴（轴角）(axis angle)
[3]欧拉角(euler angles)
[4]四元数(quaternion)**

在这里插入图片描述
主动旋转和被动旋转：主动旋转是指将向量或坐标系逆时针围绕旋转轴旋转，被动旋转是对坐标轴进行的逆时针旋转，相当于主动旋转的逆操作。

2 rotate函数

rotate是matlab官方提供的三维旋转图形函数。
rotate通过给定轴角，使用下列公式转换得到旋转矩阵R，再通过R得到旋转后的图像：
在这里插入图片描述
rotate(h,direction,alpha,origin)

[1]h是绘制对象。
[2]direction 是一个二元素或三元素向量，它与旋转轴原点共同确定旋转轴。
[3]direction 二元素形式中，theta 是 x 的正轴在 x-y 平面中的逆时针角度。phi 是方向向量在 x-y 平面中的仰角。
[4]direction 三元素形式中，指定使用笛卡尔坐标的轴方向，也就是XYZ轴。方向向量是从旋转原点到 P 的向量。
[5]alpha是旋转角度。
[6]origin是旋转轴原点，默认（0，0，0），是可选参数。
[7]旋转轴由direction(对它进行归一化处理后得到的点P)和origin(旋转原点)共同确定。

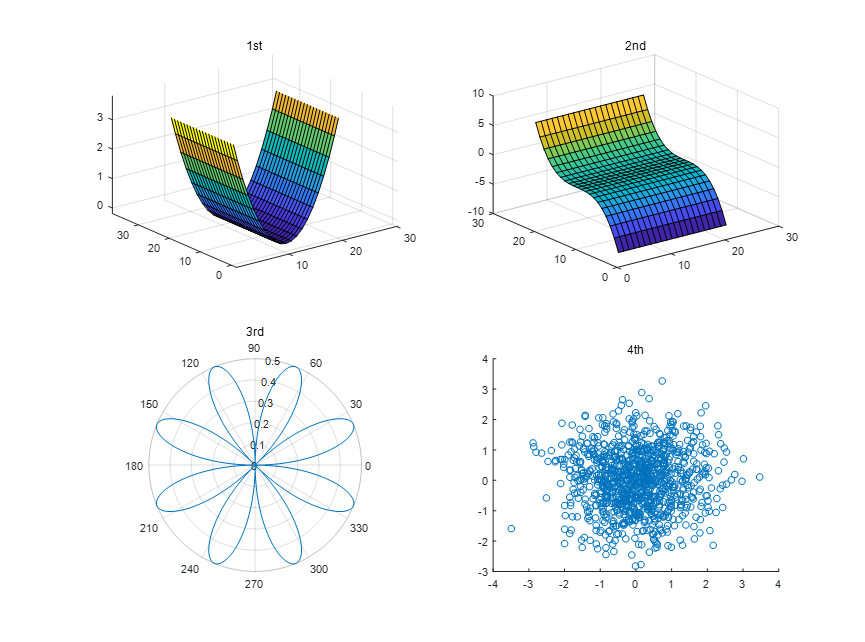
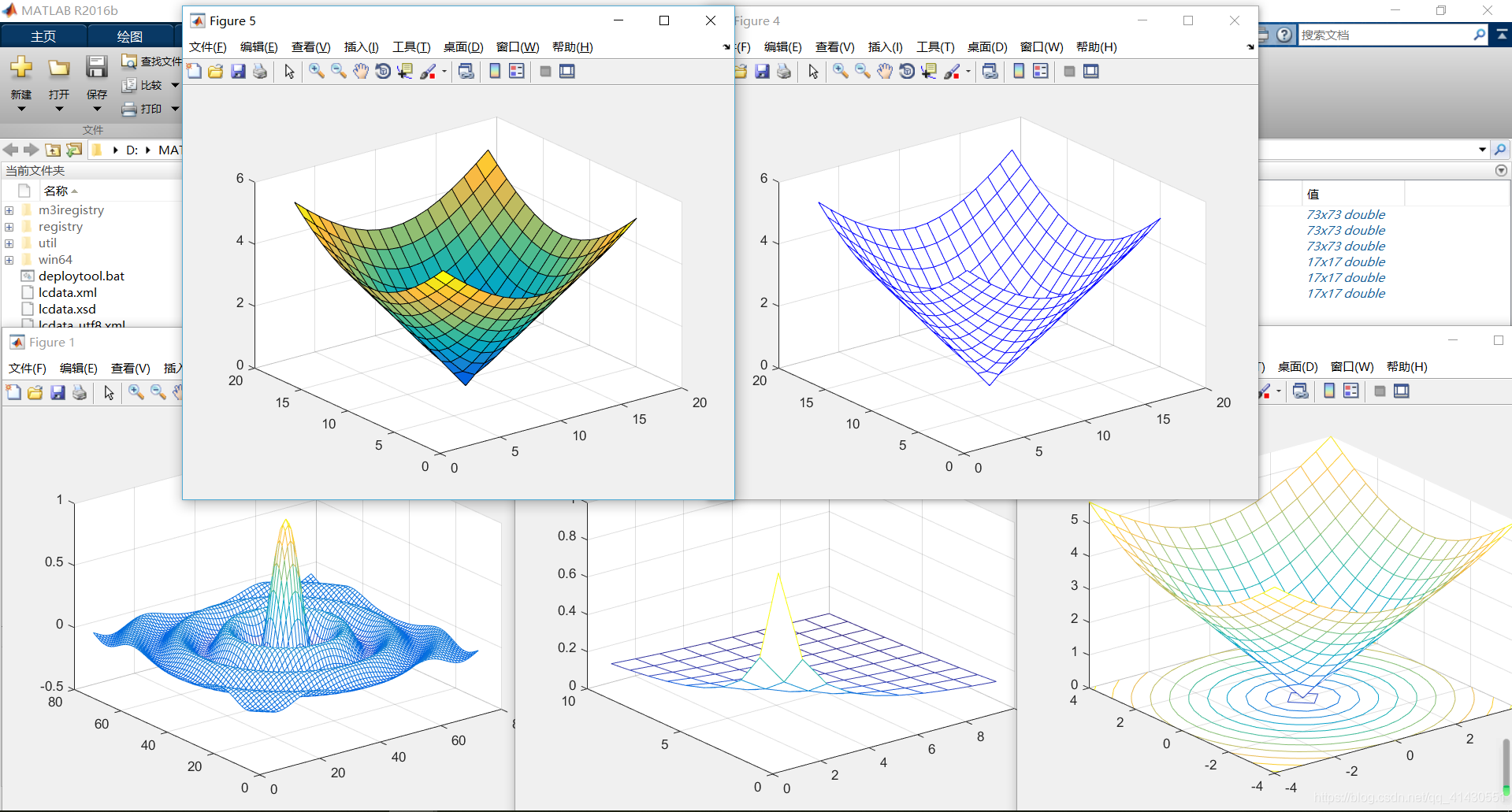
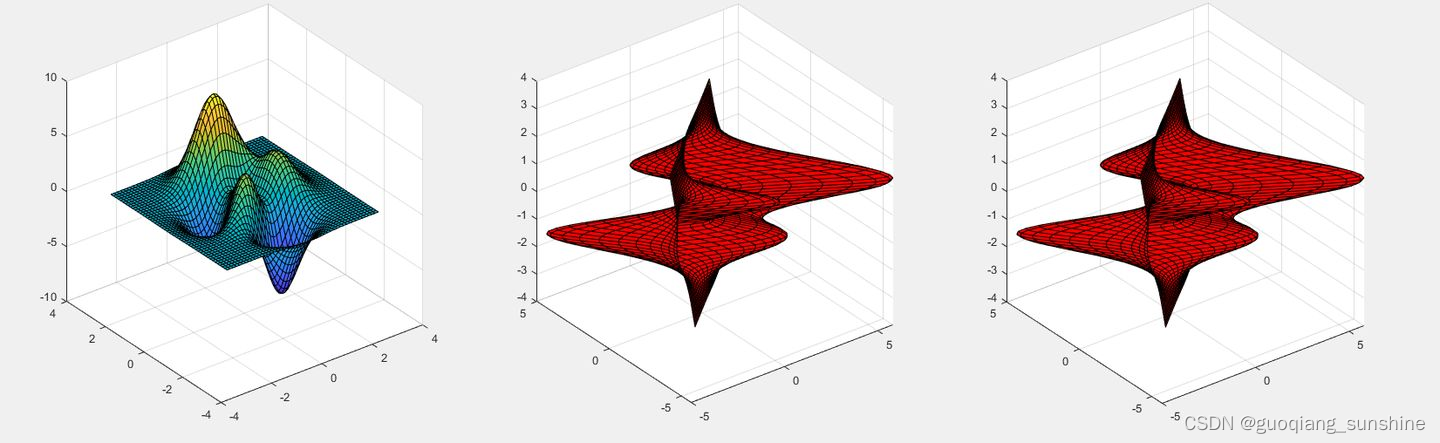
示例单绕「旋转轴」为「坐标轴」旋转:

clc;
clear;[X,Y,Z] = peaks;%
subplot(1,2,1)
surf(X,Y,Z);
title("原始");%
subplot(1,2,2)
h=surf(X,Y,Z);
rotate(h,[1,0,0],90,[0,0,0]);
title("官方函数，绕X轴，逆时针旋转90°");%matlab绘图运用右手坐标系。
%在右手坐标系中，旋转角的正方向为逆时针方向。

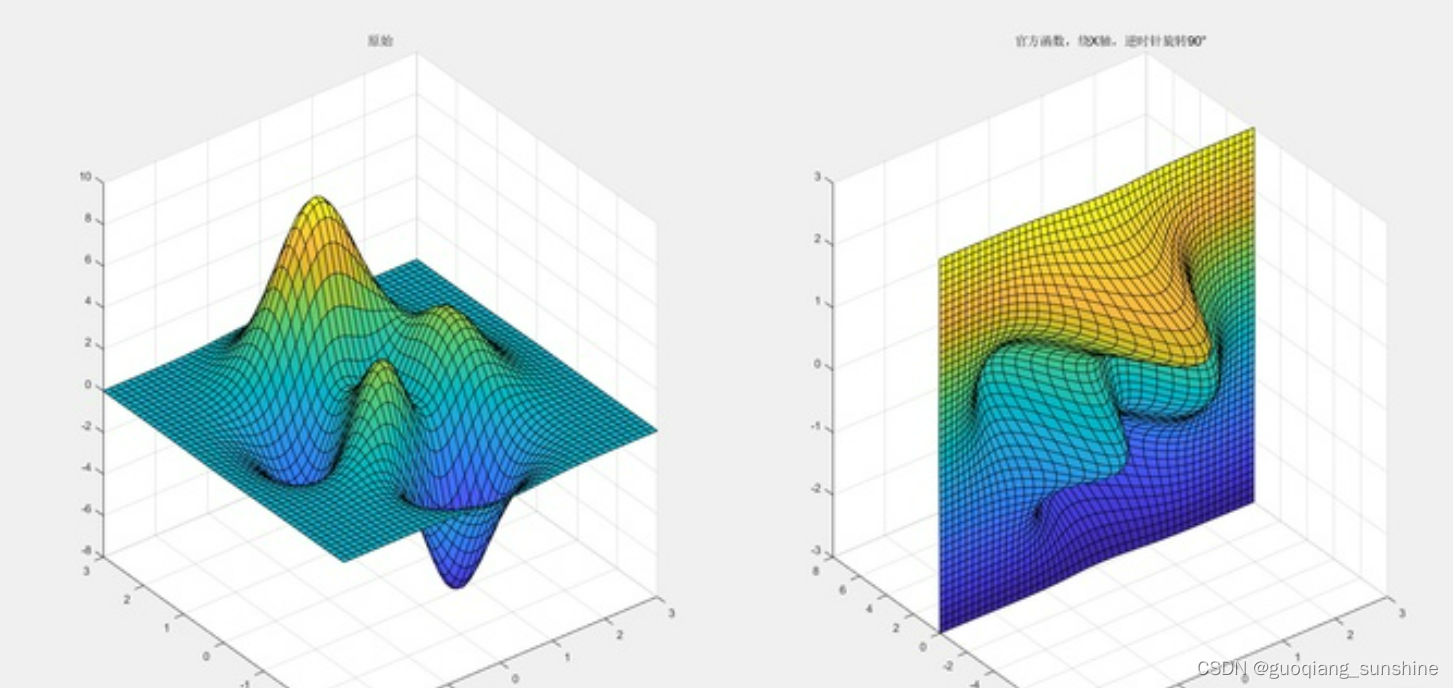
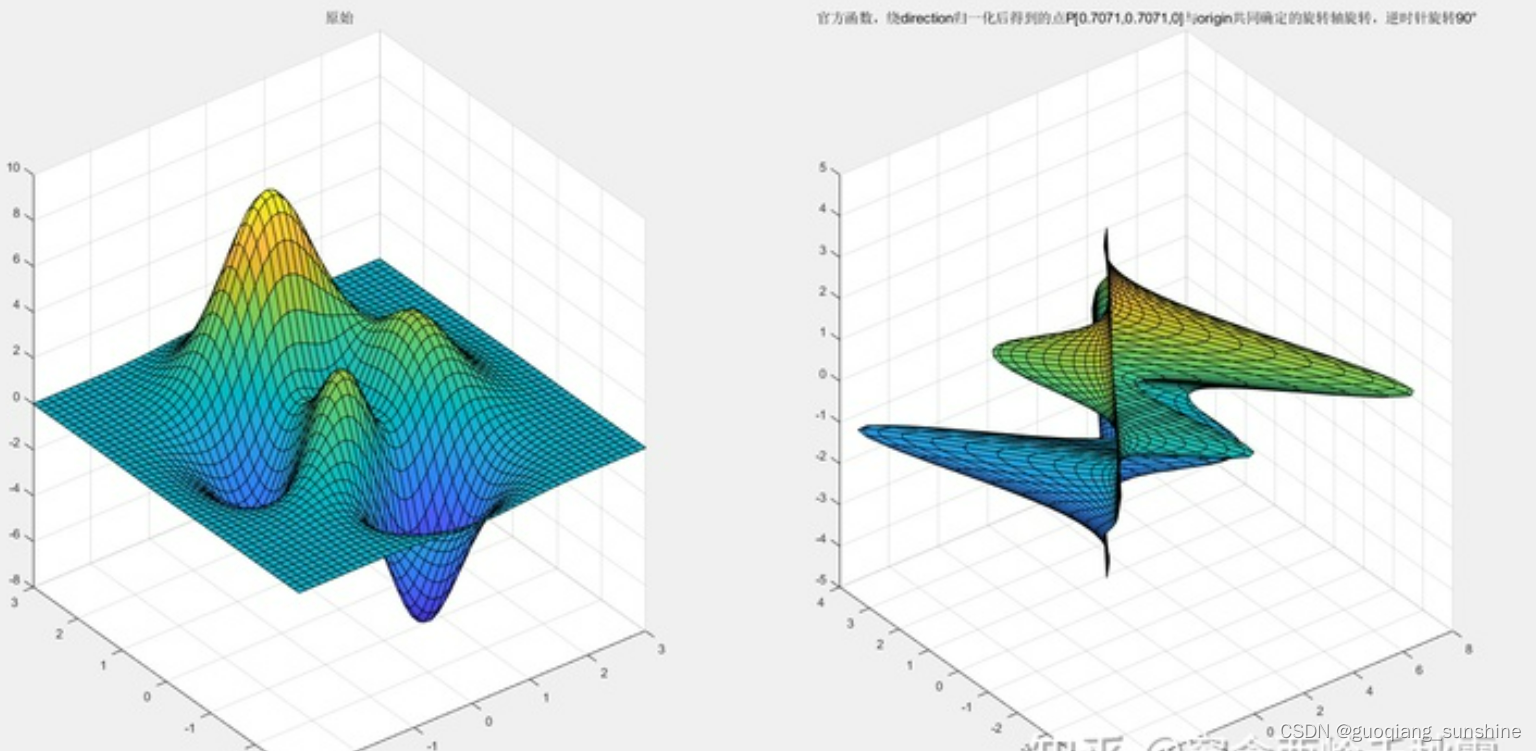
在这里插入图片描述
示例单绕「旋转轴」为「任意轴」旋转:

clc;
clear;[X,Y,Z] = peaks;%
subplot(1,2,1)
surf(X,Y,Z);
title("原始");%
subplot(1,2,2)
h=surf(X,Y,Z);
direction=[1,1,0];
origin=[0,0,0];
rotate(h,direction,90,origin);
title("官方函数，绕direction归一化后得到的点P[0.7071,0.7071,0]与origin共同确定的旋转轴旋转，逆时针旋转90°");%[1]注意，这条旋转轴不再是某条坐标轴了。
%[2]踩坑提示，千万不要认为[1,1,0],90是指先绕x轴旋转90°再绕y轴旋转90°,可能被官方文档一处例子误导。
%[3]向量归一化指[向量中的每个元素]依次除以该[向量的模]，使该向量成为单位向量，单位向量是指模等于1的向量，方向任意，有无数个。
%[4]单位向量=原向量(:)/norm(原向量);
%[5]rotate源码第44行计算点P也就是u。
%[6]官方函数无法原文档编辑，可以复制一份到自建.m文件即可编辑。

在这里插入图片描述
示例连绕「旋转轴」为「坐标轴」旋转:

clc;
clear;[X,Y,Z] = peaks;%
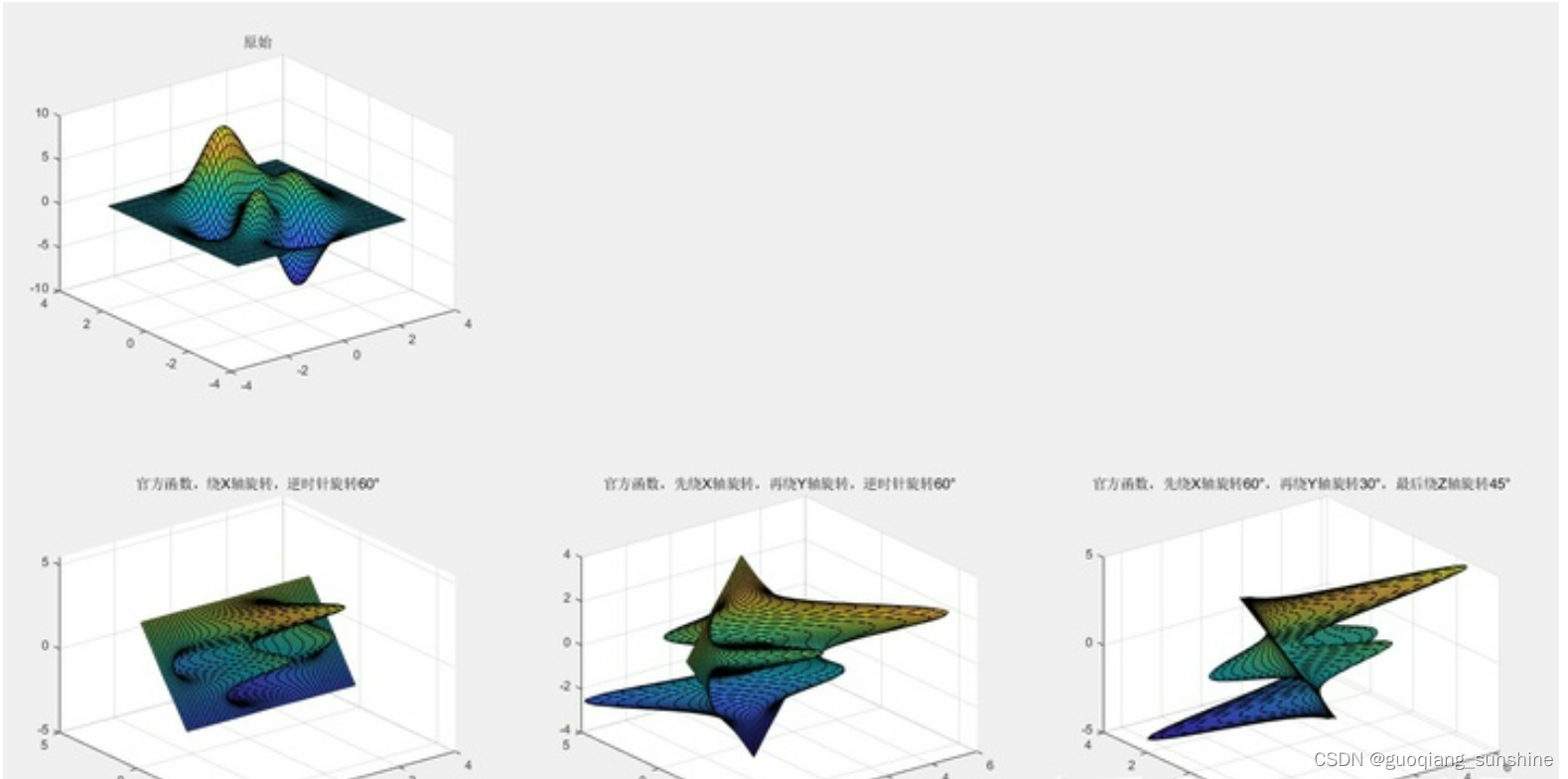
subplot(2,3,1)
surf(X,Y,Z);
title("原始");%
subplot(2,3,4)
h1=surf(X,Y,Z);
rotate(h1,[1,0,0],60,[0,0,0]);
title("官方函数，绕X轴旋转，逆时针旋转60°");%
subplot(2,3,5)
h2=surf(X,Y,Z);
rotate(h2,[1,0,0],60,[0,0,0]);
rotate(h2,[0,1,0],60,[0,0,0]);
title("官方函数，先绕X轴旋转，再绕Y轴旋转，逆时针旋转60°");%
subplot(2,3,6)
h3=surf(X,Y,Z);
rotate(h3,[1,0,0],60,[0,0,0]);
rotate(h3,[0,1,0],30,[0,0,0]);
rotate(h3,[0,0,1],45,[0,0,0]);
title("官方函数，先绕X轴旋转60°，再绕Y轴旋转30°，最后绕Z轴旋转45°");

在这里插入图片描述
rotate源码：

function rotate(h,azel,alpha,origin)
%ROTATE Rotate objects about specified origin and direction.
%   ROTATE(H,[THETA PHI],ALPHA) rotates the objects with handles H
%   through angle ALPHA about an axis described by the 2-element
%   direction vector [THETA PHI] (spherical coordinates).  
%   All the angles are in degrees.  The handles in H must be children
%   of the same axes.
%
%   THETA is the angle in the xy plane counterclockwise from the
%   positive x axis.  PHI is the elevation of the direction vector
%   from the xy plane (see also SPH2CART).  Positive ALPHA is defined
%   as the righthand-rule angle about the direction vector as it
%   extends from the origin.
%
%   ROTATE(H,[X Y Z],ALPHA) rotates the objects about the direction
%   vector [X Y Z] (Cartesian coordinates). The direction vector
%   is the vector from the center of the plot box to (X,Y,Z).
%
%   ROTATE(...,ORIGIN) uses the point ORIGIN = [x0,y0,z0] as
%   the center of rotation instead of the center of the plot box.
%
%   See also SPH2CART, CART2SPH.%   Copyright 1984-2017 The MathWorks, Inc.% Determine the default origin (center of plot box).
if nargin < 4if ~isgraphics(h)error(message('MATLAB:rotate:InvalidHandle'));endax = ancestor(h(1),'axes');if isempty(ax) || ax==0error(message('MATLAB:rotate:InvalidHandle'));endorigin = sum([get(ax,'xlim')' get(ax,'ylim')' get(ax,'zlim')'])/2;
end% find unit vector for axis of rotation
if numel(azel) == 2 % theta, phitheta = pi*azel(1)/180;phi = pi*azel(2)/180;u = [cos(phi)*cos(theta); cos(phi)*sin(theta); sin(phi)];
elseif numel(azel) == 3 % direction vectoru = azel(:)/norm(azel);
endalph = alpha*pi/180;
cosa = cos(alph);
sina = sin(alph);
vera = 1 - cosa;
x = u(1);
y = u(2);
z = u(3);
rot = [cosa+x^2*vera x*y*vera-z*sina x*z*vera+y*sina; ...x*y*vera+z*sina cosa+y^2*vera y*z*vera-x*sina; ...x*z*vera-y*sina y*z*vera+x*sina cosa+z^2*vera]';for i=1:numel(h)t = get(h(i),'type');skip = 0;if strcmp(t,'surface') || strcmp(t,'line') || strcmp(t,'patch')% If patch, rotate vertices  if strcmp(t,'patch')verts = get(h(i),'Vertices');x = verts(:,1); y = verts(:,2); if size(verts,2)>2z = verts(:,3);elsez = [];end% If surface or line, rotate {x,y,z}data   elsex = get(h(i),'xdata');y = get(h(i),'ydata');z = get(h(i),'zdata');endif isempty(z)z = -origin(3)*ones(size(y));end[m,n] = size(z);if numel(x) < m*n[x,y] = meshgrid(x,y);endelseif strcmp(t,'text')p = get(h(i),'position');x = p(1); y = p(2); z = p(3);elseif strcmp(t,'image')x = get(h(i),'xdata');y = get(h(i),'ydata');z = zeros(size(x));elseskip = 1;endif ~skip[m,n] = size(x);newxyz = [x(:)-origin(1), y(:)-origin(2), z(:)-origin(3)];newxyz = newxyz*rot;newx = origin(1) + reshape(newxyz(:,1),m,n);newy = origin(2) + reshape(newxyz(:,2),m,n);newz = origin(3) + reshape(newxyz(:,3),m,n);if strcmp(t,'surface') || strcmp(t,'line')set(h(i),'xdata',newx,'ydata',newy,'zdata',newz);elseif strcmp(t,'patch')set(h(i),'Vertices',[newx,newy,newz]); elseif strcmp(t,'text')set(h(i),'position',[newx newy newz])elseif strcmp(t,'image')set(h(i),'xdata',newx,'ydata',newy)endend
end

造轮子，实现与rotate一样功能的函数MyRotate()：

clc;
clear;[X,Y,Z] = peaks;subplot(2,3,1)
surf(X,Y,Z);
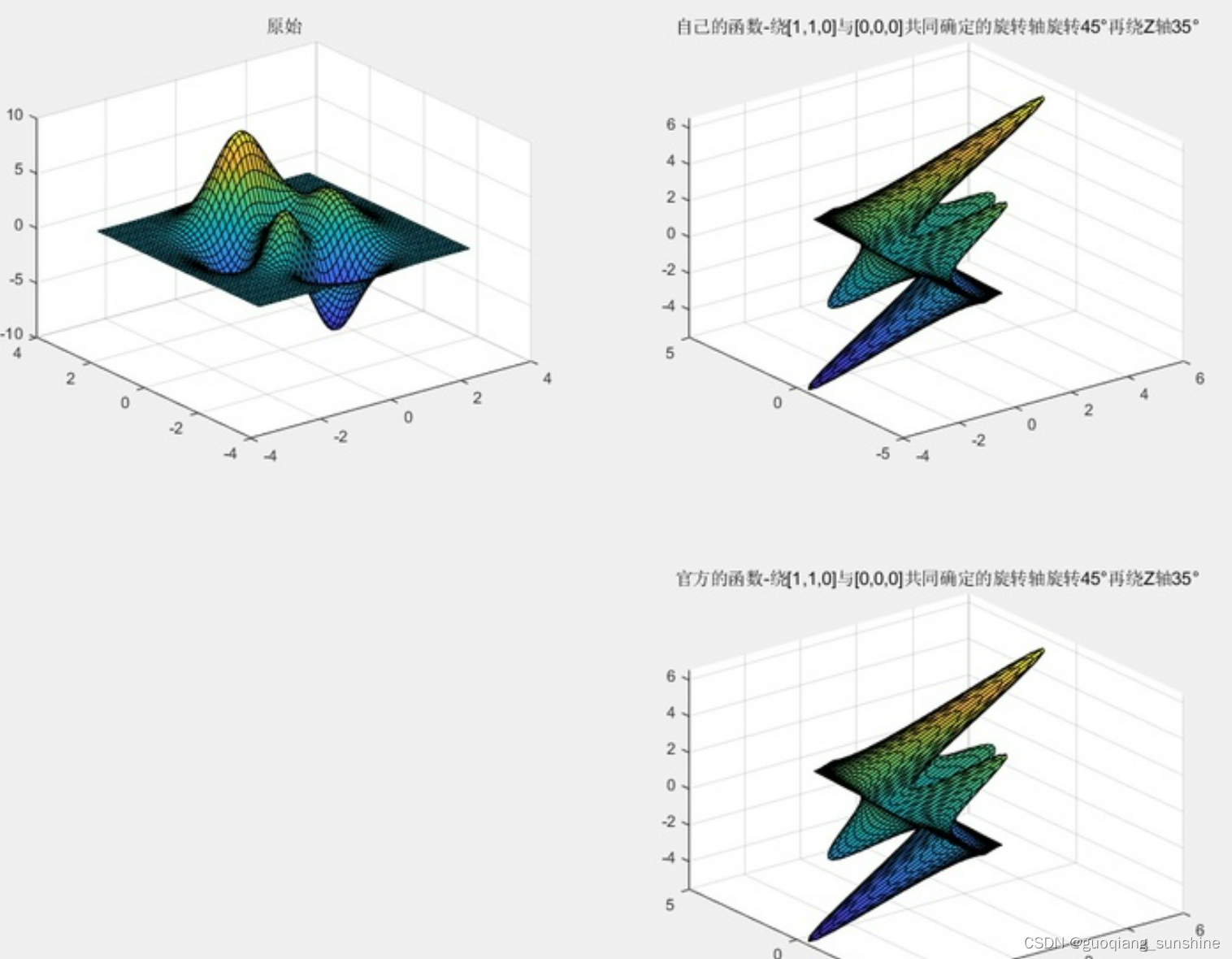
title("原始");subplot(2,3,2)
[VnewX,VnewY,VnewZ]=MyRotate(X,Y,Z            ,[1,1,0],45,[0,0,0]);
[VnewX,VnewY,VnewZ]=MyRotate(VnewX,VnewY,VnewZ,[0,0,1],35,[0,0,0]);
surf(VnewX,VnewY,VnewZ);
title("自己的函数-绕[1,1,0]与[0,0,0]共同确定的旋转轴旋转45°再绕Z轴35°");subplot(2,3,5)
h=surf(X,Y,Z);
rotate2(h,[1,1,0],45,[0,0,0]);
rotate2(h,[0,0,1],35,[0,0,0]);
title("官方的函数-绕[1,1,0]与[0,0,0]共同确定的旋转轴旋转45°再绕Z轴35°");function [VnewX,VnewY,VnewZ]=MyRotate(X,Y,Z,r,alpha,origin)%if numel(r) == 2r_theta = pi*r(1)/180;r_phi   = pi*r(2)/180;r     = [cos(r_phi)*cos(r_theta); cos(r_phi)*sin(r_theta); sin(r_phi)];elseif numel(r) == 3r = r(:)/norm(r);end%theta=deg2rad(alpha);%XYZ=[X(:),Y(:),Z(:)];%Vnew=zeros(size(XYZ));%罗德里格旋转公式for i=1:1:size(XYZ,1)V=XYZ(i,:);V=[V(1,1)-origin(1), V(1,2)-origin(2), V(1,3)-origin(3)];Vnew(i,:) = cos(theta)*V + (1-cos(theta))*dot(r,V)*r' + sin(theta)*cross(r,V);end%VnewX = origin(1) + reshape(Vnew(:,1),size(X));VnewY = origin(2) + reshape(Vnew(:,2),size(Y));VnewZ = origin(3) + reshape(Vnew(:,3),size(Z));
end

在这里插入图片描述

3 旋转矩阵

三维旋转矩阵是一个3x3的正交矩阵。一个向量乘以旋转矩阵等价于向量以某种方式进行旋转。

%若已经得当旋转矩阵rot,且x,y,z为图形未旋转的数据,则通过与rot旋转矩阵相乘即可得到图形旋转后的数据。
%origin是旋转轴原点，默认(0,0,0），不指定可忽略。origin=[0,0,0];newxyz = [x(:)-origin(1), y(:)-origin(2), z(:)-origin(3)];
newxyz = newxyz*rot;newx = origin(1) + reshape(newxyz(:,1),m,n);
newy = origin(2) + reshape(newxyz(:,2),m,n);
newz = origin(3) + reshape(newxyz(:,3),m,n);

旋转向量与旋转矩阵可以通过罗德里格斯(Rodrigues)变换进行转换。
通常计算图形的旋转，都是转化为旋转矩阵来计算，各类三维旋转描述方式之间的转换关系如下：
下图参考知乎：
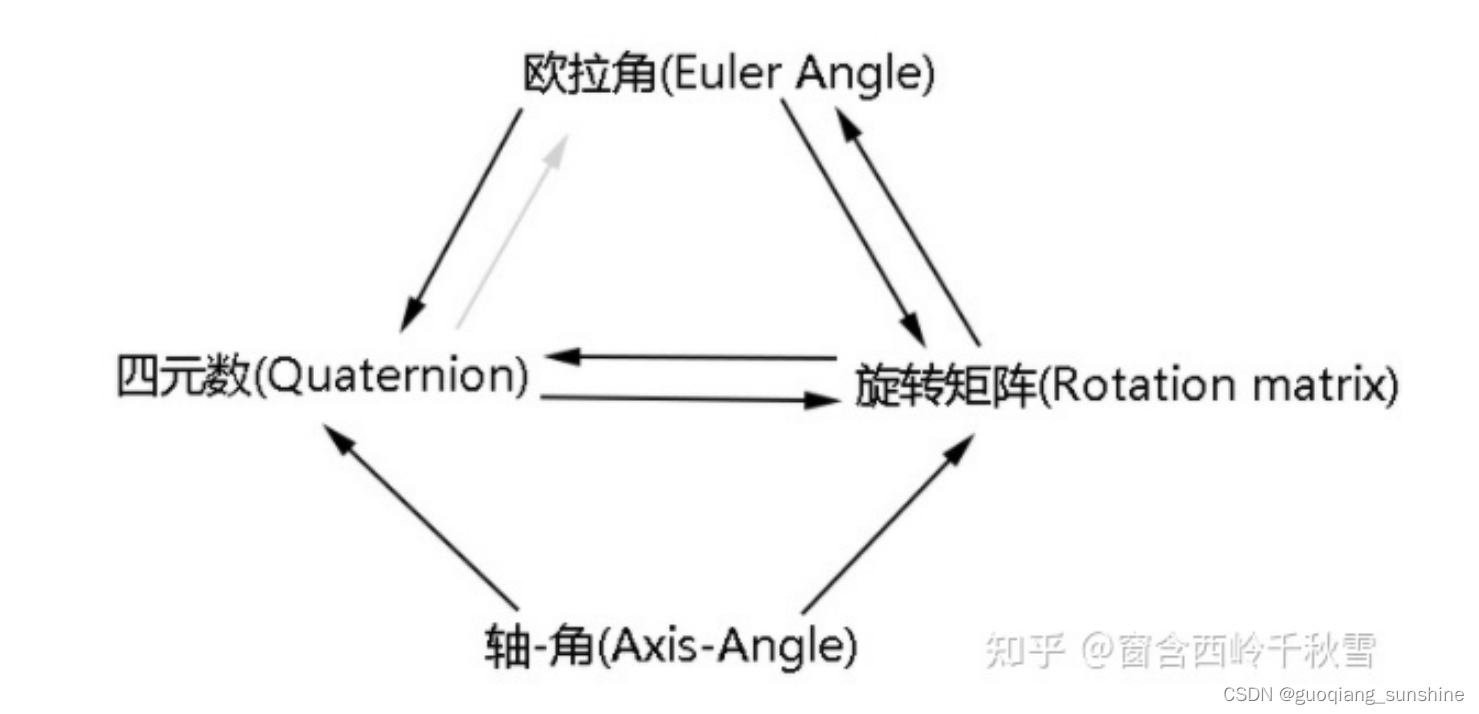
在这里插入图片描述
MATLAB官方提供的转换到旋转矩阵函数：

eul2rotm()  --欧拉角        转 旋转矩阵
axang2rotm()--旋转向量/轴角 转 旋转矩阵
quat2rotm() --四元数        转 旋转矩阵

4 旋转向量/轴角

旋转向量也称为轴角。
旋转向量是指用一个三维向量来表示三维旋转变换，该向量的方向是旋转轴，其模则是旋转角度。其描述一个坐标系沿某一条直线(或轴)旋转一定的角度，能与另一个坐标系重合。
MATLAB官方提供了旋转向量与旋转矩阵相互转换的函数：

rotationVectorToMatrix()
rotationMatrixToVector()

在这里插入图片描述
通过旋转向量/轴角也可直接求图形旋转后的位置，使用罗德里格旋转公式的其中一种形式，公式为：

代码示例：

clc;
clear;[X,Y,Z] =  peaks;subplot(1,3,1)
surf(X,Y,Z);
title("原始");
axis squaresubplot(1,3,2)
[VnewX,VnewY,VnewZ]=AxisAngleRotate(X,Y,Z            ,[1,0,0],90);
[VnewX,VnewY,VnewZ]=AxisAngleRotate(VnewX,VnewY,VnewZ,[0,1,0],25);
surf(VnewX,VnewY,VnewZ);
title("自己的函数-先绕X轴旋转90°再绕Y轴旋转25°");
axis squaresubplot(1,3,3)
h=surf(X,Y,Z);
rotate(h,[1,0,0],90,[0,0,0]);
rotate(h,[0,1,0],25,[0,0,0]);
title("官方的函数-先绕X轴旋转90°再绕Y轴旋转25°");
axis squarefunction [VnewX,VnewY,VnewZ]=AxisAngleRotate(X,Y,Z,direction,alpha)%r是旋转向量，其方向是旋转轴，其模则是旋转角度。r=deg2rad(alpha)*direction;%旋转角度theta=norm(r);%归一化且转置,公式中要求r为单位向量r=r(:)/norm(r);r=r';%XYZ=[X(:),Y(:),Z(:)];%Vnew=zeros(size(XYZ));%通过旋转向量直接求图形旋转后的位置for i=1:1:length(XYZ)V=XYZ(i,:);Vnew(i,:) = cos(theta)*V + (1-cos(theta))*dot(r,V)*r + sin(theta)*cross(r,V);end%VnewX = reshape(Vnew(:,1),size(X));VnewY = reshape(Vnew(:,2),size(Y));VnewZ = reshape(Vnew(:,3),size(Z));
end

在这里插入图片描述

5 欧拉角

在三维空间中，物体的旋转可由三个欧拉角表示：

pitch 围绕X轴旋转，叫俯仰角。 
yaw   围绕Y轴旋转，叫偏航角。 
roll  围绕Z轴旋转，叫翻滚角。

在这里插入图片描述
欧拉旋转的本质是将绕任意轴旋转最终分解为绕x，y，z轴的旋转，存在万向节死锁问题。而四元数旋转可直接表示为绕任意轴旋转，则不存在此问题。
欧拉角的“万向节死锁”问题，是由于欧拉旋转定义本身造成的。这种围绕选旋转前固定轴的先Z、再X、再Y的旋转操作，与其最终所预期的三个轴向可以旋转的结果并非一定是一对一的映射。某些情况下是多对一的映射，造成一些旋转自由度的缺失，也就是“死锁”。

通过欧拉角公式也可直接求图形旋转后的位置，公式如下：
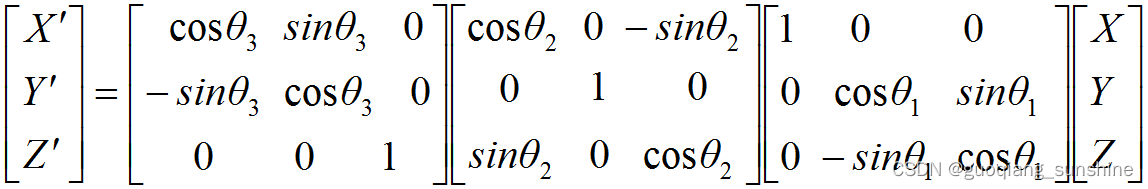
在这里插入图片描述
代码示例：

%%
clc;
clear;
%%
[X,Y,Z] = peaks;
%%
subplot(1,3,1)
surf(X,Y,Z);
title("原始");
axis square
%%
subplot(1,3,2)
h=surf(X,Y,Z);
rotate(h,[1,0,0],55,[0,0,0]);
rotate(h,[0,1,0],77,[0,0,0]);
title("官方的函数-X轴旋转55°再Y轴旋转77°");
axis square
%%
subplot(1,3,3)
[Xnew,Ynew,Znew]=EulerAnglesRotate(X,Y,Z,[55,77,0]);
surf(Xnew,Ynew,Znew);
title("自己的函数-X轴旋转55°再Y轴旋转77°");
axis square
%%
function [Xnew,Ynew,Znew]=EulerAnglesRotate(Xdata,Ydata,Zdata,alpha)%thetaX = deg2rad(360 - alpha(1));thetaY = deg2rad(360 - alpha(2));thetaZ = deg2rad(360 - alpha(3));%XYZ=[Xdata(:),Ydata(:),Zdata(:)];XYZnew=zeros(size(XYZ));%for i=1:1:length(XYZ)%curX=XYZ(i,1);curY=XYZ(i,2);curZ=XYZ(i,3);%PartZ=[cos(thetaZ),sin(thetaZ),0;-sin(thetaZ),cos(thetaZ),0;0,0,1];PartY=[cos(thetaY),0,-sin(thetaY);0,1,0;sin(thetaY),0,cos(thetaY)];PartX=[1,0,0;0,cos(thetaX),sin(thetaX);0,-sin(thetaX),cos(thetaX)];PartXYZ=[curX;curY;curZ];%XYZnew(i,:)=PartZ*PartY*PartX*PartXYZ;end%Xnew=reshape(XYZnew(:,1),size(Xdata));Ynew=reshape(XYZnew(:,2),size(Ydata));Znew=reshape(XYZnew(:,3),size(Zdata));
end

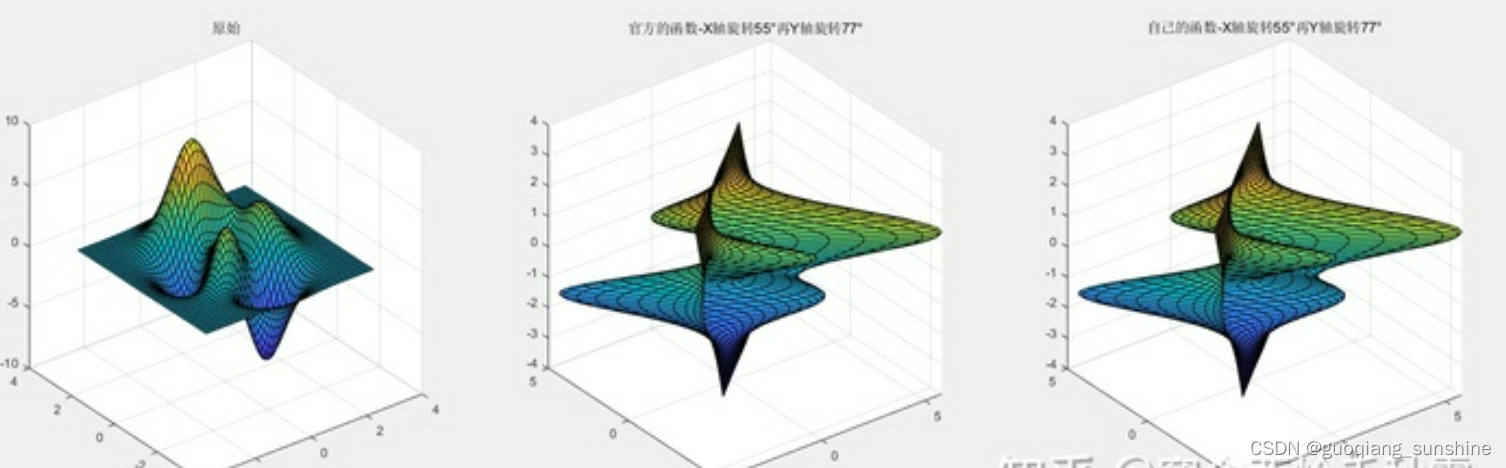
在这里插入图片描述
另外再提一种简单的欧拉角旋转公式，如下：

代码示例：

%%
clc;
clear;
%%
[X,Y,Z] = peaks;
%%
subplot(1,3,1)
surf(X,Y,Z);
title("原始");
axis square
%%
subplot(1,3,2)
h=surf(X,Y,Z);
rotate(h,[1,0,0],30,[0,0,0]);
rotate(h,[0,1,0],45,[0,0,0]);
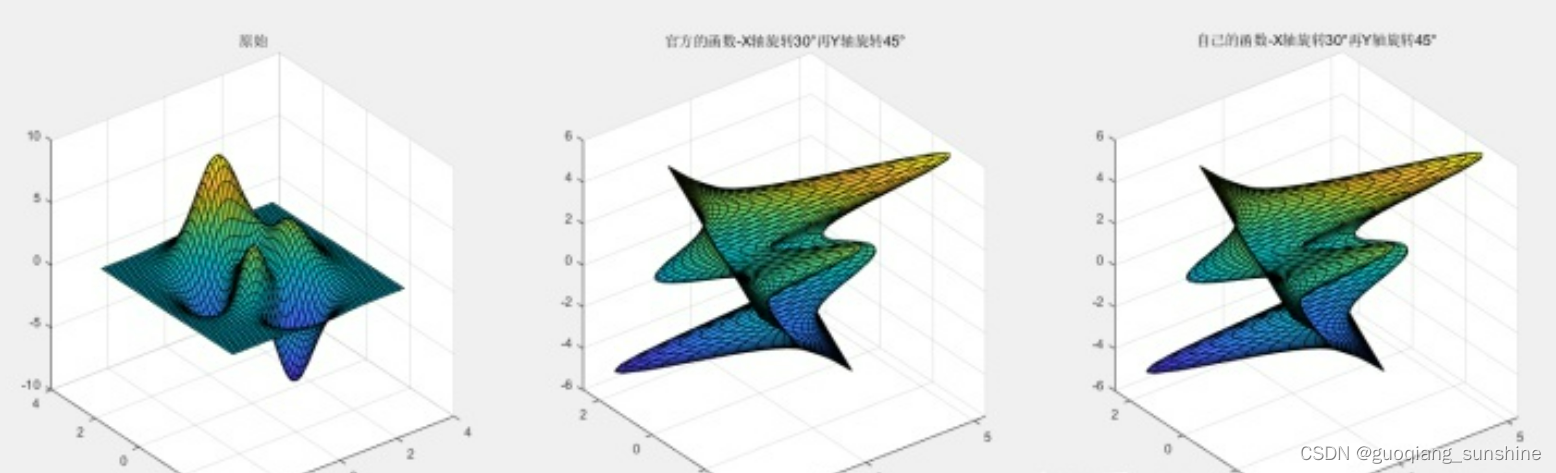
title("官方的函数-X轴旋转30°再Y轴旋转45°");
axis square
%%
subplot(1,3,3)
[Xnew,Ynew,Znew]=AxisAngleRotate2(X,Y,Z,[1,1,0],[30,45,0]);
surf(Xnew,Ynew,Znew);
title("自己的函数-X轴旋转30°再Y轴旋转45°");
axis square
%%
function [Xnew,Ynew,Znew]=AxisAngleRotate2(Xdata,Ydata,Zdata,direction,alpha)%thetaX = deg2rad(alpha(1));thetaY = deg2rad(alpha(2));thetaZ = deg2rad(alpha(3));%绕X轴旋转if direction(1)==1Y_x = Ydata*cos(thetaX) - Zdata*sin(thetaX);Z_x = Ydata*sin(thetaX) + Zdata*cos(thetaX);%Ydata=Y_x;Zdata=Z_x;end%绕Y轴旋转if direction(2)==1X_y = Xdata*cos(thetaY) + Zdata*sin(thetaY);Z_y = Zdata*cos(thetaY) - Xdata*sin(thetaY);%Xdata=X_y;Zdata=Z_y;end%绕Z轴旋转if direction(3)==1X_z = Xdata*cos(thetaZ) - Ydata*sin(thetaZ);Y_z = Xdata*sin(thetaZ) + Ydata*cos(thetaZ);%Xdata=X_z;Ydata=Y_z;end%Xnew=Xdata;Ynew=Ydata;Znew=Zdata;
end

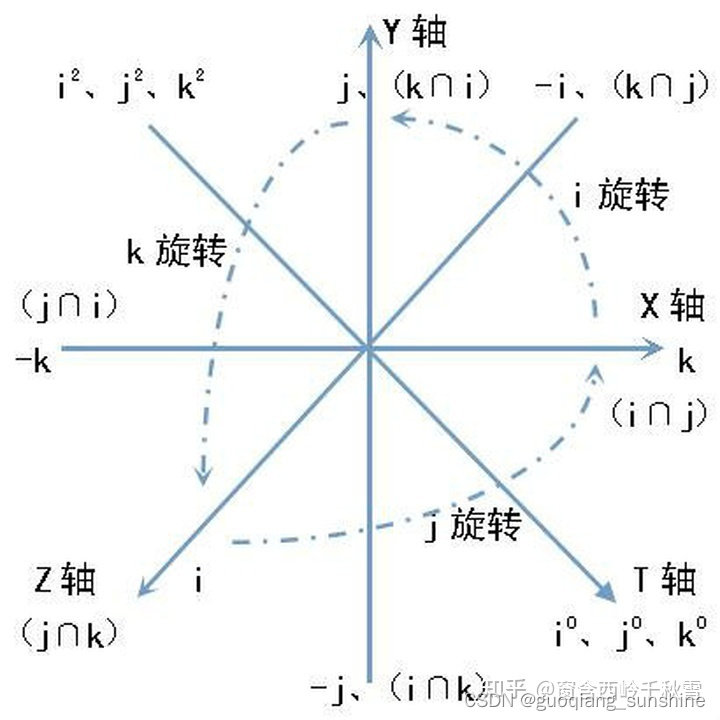
在这里插入图片描述

6 四元数

在这里插入图片描述
四元数是简单的超复数。复数是由实数加上虚数单位 i 组成，其中i^2 = -1。相似地，四元数都是由实数加上三个虚数单位 i、j、k 组成，而且它们有如下的关系： i^2 = j^2 = k^2 = -1， i^0 = j^0 = k^0 = 1 , 每个四元数都是 1、i、j 和 k 的线性组合，即是四元数一般可表示为a + bi+ cj + dk，其中a、b、c 、d是实数。
对于i、j、k本身的几何意义可以理解为一种旋转，其中i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转，j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转，k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转，-i、-j、-k分别代表i、j、k旋转的反向旋转。
四元数的用途仍在争辩之中。一些哈密顿的支持者非常反对奥利弗·亥维赛（Oliver Heaviside）的向量代数学和约西亚·威拉德·吉布斯（Josiah Willard Gibbs）的向量微积分的发展，以维持四元数的超然地位。对于三维空间这可以讨论，但对于更高维四元数就失效了（但可用延伸如八元数和柯利弗德代数学）。而事实上，在二十世纪中叶的科学和工程界中，向量几乎已完全取代四元数的位置。