238. 银河英雄传说 - AcWing题库

题意：

思路：

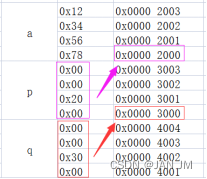
并查集维护两个信息：每个连通块的size和每个结点之间的距离

对于连通块的size，只需要在合并的时候维护一下就好了

对于每个结点之间的距离，我们考虑类似于树上差分的思想，先处理每个结点离根节点的距离，再差分减一下就好了

那么问题就转化成维护每个结点离根节点的距离

由于维护的信息的主体是结点，那么就不能只在合并的时候维护了，在find的时候也需要维护

我们将连通块v接到连通块u下面时，更新连通块v的每个结点离根节点的距离，因为根节点换了，同时也要更新连通块的size

更新连通块v每个结点的信息是通过find回溯的时候更新的，我们给u的原先的根节点+=size(u)就行，这样在之后如果访问连通块v的某个结点时，find在回溯时会把这个结点和连通块v原先根节点之间的所有结点都更新，同时也将这些结点路径压缩，这有点像线段树懒标记的感觉

路径压缩后，虽然原先的链式结构被破坏，但是距离信息保留在d数组中，因此查询的时候直接查询d[x]就好了，d数组相当于是前缀和数组

如果之后又要合并已经被路径压缩的结点，也是同样的道理，先更新连通块根节点（相当于打个标记），然后在查询的时候回溯下传求前缀和就好了

Code：

#include <bits/stdc++.h>
using namespace std;
const int mxn=3e4+10;
string op;
int n,x,y;
int f[mxn],sz[mxn],d[mxn];
int find(int x){if(f[x]!=x){int rt=find(f[x]);d[x]+=d[f[x]];f[x]=rt;}return f[x];
}
void join(int u,int v){int f1=find(u),f2=find(v);if(f1!=f2){f[f1]=f2;d[f1]=sz[f2];sz[f2]+=sz[f1];}
}
int main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin>>n;for(int i=1;i<mxn;i++) f[i]=i,sz[i]=1;for(int i=1;i<=n;i++){cin>>op>>x>>y;if(op=="M"){join(x,y);}else{int a=find(x),b=find(y);if(a!=b) cout<<-1<<'\n';else cout<<max(0,abs(d[x]-d[y])-1)<<'\n';}}
}

总结：

当要我们维护联通块信息、涉及到分类、判环、维护传递性关系时都可以用并查集

在写并查集之前先考虑好并查集维护的对象

并查集维护两种信息：连通块信息和结点信息

维护连通块信息时，只需在合并的时候维护就好了，维护完连通块之后可以考虑缩点

维护结点信息时，要在find和merge时一起维护，在merge的时候给根节点打标记，在find的时候回溯下传标记