很久之前做了C3D的视频分类，现在详细把整个项目的细节描述一下。
首先介绍一下C3D：对于一段视频来说，它是连续的帧图像叠加起来的，所以可以考虑在生成通道图像的时候，把多帧图像叠加的特性讨论进去。

一个视频段输入，其大小为 c∗l∗h∗w ,其中c为图像通道(一般为3),l为视频序列的长度，h和w分别为视频的宽与高。进行一次kernel size为3∗3∗3,stride为1,padding=True,滤波器个数为K的3D 卷积后，输出的大小为K∗l∗h∗w。池化同理。

作者对卷积核做了研究，发现3*3的卷积核最有效。基于3D卷积操作，共有8次卷积操作，4次池化操作。其中卷积核的大小均为3∗3∗3，步长为1∗1∗1。池化核的大小为2∗2∗2,步长为2∗2∗2，但第一层池化除外，其大小和步长均为1∗2∗2。这是为了不过早缩减时序上的长度。最终网络在经过两次全连接层和softmax层后就得到了最终的输出结果。网络的输入尺寸为3∗16∗112∗112，即一次输入16帧图像。
github地址：https://github.com/hx173149/C3D-tensorflow
训练过程：首先按照train.list，test.list将文件分类。然后使用ffmpeg，将视频分割，这里每5帧取一张图片。
模型代码：

def conv3d(name, l_input, w, b):  	return tf.nn.bias_add(            tf.nn.conv3d(l_input, w, strides=[1, 1, 1, 1, 1], padding='SAME'),          b          )def max_pool(name, l_input, k):   
return tf.nn.max_pool3d(l_input, ksize=[1, k, 2, 2, 1], strides=[1, k, 2, 2, 1], padding='SAME', name=name)def inference_c3d(_X, _dropout, batch_size, _weights, _biases):# Convolution Layer  conv1 = conv3d('conv1', _X, _weights['wc1'], _biases['bc1'])  conv1 = tf.nn.relu(conv1, 'relu1')  pool1 = max_pool('pool1', conv1, k=1)# Convolution Layer  conv2 = conv3d('conv2', pool1, _weights['wc2'], _biases['bc2'])  conv2 = tf.nn.relu(conv2, 'relu2')  pool2 = max_pool('pool2', conv2, k=2)# Convolution Layer  conv3 = conv3d('conv3a', pool2, _weights['wc3a'], _biases['bc3a'])  conv3 = tf.nn.relu(conv3, 'relu3a')  conv3 = conv3d('conv3b', conv3, _weights['wc3b'], _biases['bc3b'])  conv3 = tf.nn.relu(conv3, 'relu3b')  pool3 = max_pool('pool3', conv3, k=2)# Convolution Layer  conv4 = conv3d('conv4a', pool3, _weights['wc4a'], _biases['bc4a'])  conv4 = tf.nn.relu(conv4, 'relu4a')  conv4 = conv3d('conv4b', conv4, _weights['wc4b'], _biases['bc4b'])  conv4 = tf.nn.relu(conv4, 'relu4b')  pool4 = max_pool('pool4', conv4, k=2)# Convolution Layer  conv5 = conv3d('conv5a', pool4, _weights['wc5a'], _biases['bc5a'])  conv5 = tf.nn.relu(conv5, 'relu5a')  conv5 = conv3d('conv5b', conv5, _weights['wc5b'], _biases['bc5b'])  conv5 = tf.nn.relu(conv5, 'relu5b')  pool5 = max_pool('pool5', conv5, k=2)# Fully connected layer  pool5 = tf.transpose(pool5, perm=[0,1,4,2,3])  dense1 = tf.reshape(pool5, [batch_size, _weights['wd1'].get_shape().as_list()[0]]) # Reshape conv3 output to fit dense layer input  dense1 = tf.matmul(dense1, _weights['wd1']) + _biases['bd1']dense1 = tf.nn.relu(dense1, name='fc1') # Relu activation  dense1 = tf.nn.dropout(dense1, _dropout)dense2 = tf.nn.relu(tf.matmul(dense1, _weights['wd2']) + _biases['bd2'], name='fc2') # Relu activation  dense2 = tf.nn.dropout(dense2, _dropout)# Output: class prediction  out = tf.matmul(dense2, _weights['out']) + _biases['out']return out

模型的损失函数：

def tower_loss(name_scope, logit, labels):  cross_entropy_mean = tf.reduce_mean(                  tf.nn.sparse_softmax_cross_entropy_with_logits   (labels=labels,logits=logit)                  )       #交叉熵损失函数tf.summary.scalar(                  name_scope + '_cross_entropy',                  cross_entropy_mean                  )  weight_decay_loss = tf.get_collection('weightdecay_losses')  tf.summary.scalar(name_scope + '_weight_decay_loss', tf.reduce_mean(weight_decay_loss) )# Calculate the total loss for the current tower.  total_loss = cross_entropy_mean + weight_decay_loss   tf.summary.scalar(name_scope + '_total_loss', tf.reduce_mean(total_loss) )  return total_loss

损失函数为交叉熵损失函数+regularization正则化(weight_decay)。
weight_decay:权衰量,weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，它是为了调节正则项在损失函数中占的权重。权重越大，则说明正则项对损失函数的影响越大。

另一种理解是：没有使用regularization的时候，网络训练只是通过交叉熵损失函数改变权值，这时候梯度下降的通道只有一个，当到达一定效果时，就容易在局部极小值的附近打转。增加regularization，使得改变了整个模型的梯度，跳出了局部极值的怪圈，使得整个函数目标函数分布改变了。regularization loss 的作用是不让某一权值很大，并调节其他权值，使得所有权值都相差在一定范围，使得各个神经元都能充分使用。有时需要交叉训练，比如一会儿让用于分类发loss做主导（learning_rate大，weight_decay小），有时则反过来，有时都小。

这里参数初始化的方式使用了Xavier初始化方法。

迭代更新模型的时候，使用了指数滑动平均。

variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY)  
variables_averages_op = variable_averages.apply(tf.trainable_variables())    
train_op = tf.group(apply_gradient_op1, apply_gradient_op2, variables_averages_op)

介绍一下指数滑动平均：
在采用随机梯度下降算法训练神经网络时，使用 tf.train.ExponentialMovingAverage 滑动平均操作的意义在于提高模型在测试数据上的健壮性（robustness）。在训练神经网络时，不断保持和更新每个参数的滑动平均值，在验证和测试时，参数的值使用其滑动平均值，能有效提高神经网络的准确率。

decay用于控制模型更新的速度。ExponentialMovingAverage 对每一个（待更新训练学习的）变量（variable）都会维护一个影子变量（shadow variable）。影子变量的初始值就是这个变量的初始值，
decay越大越趋于稳定。实际运用中，decay 一般会设置为十分接近 1 的常数（0.99或0.999）。为了使得模型在训练的初始阶段更新得更快，ExponentialMovingAverage 还提供了 num_updates 参数来动态设置 decay 的大小：

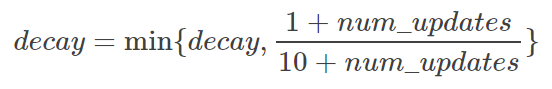
关于学习率：
这个模型把特征提取和分类分别处理

 opt_stable = tf.train.AdamOptimizer(1e-4)opt_finetuning = tf.train.AdamOptimizer(1e-3)...varlist2 = [ weights['out'],biases['out'] ]varlist1 = list( set(weights.values() + biases.values()) - set(varlist2) )...grads1 = opt_stable.compute_gradients(loss, varlist1)grads2 = opt_finetuning.compute_gradients(loss, varlist2)

在这篇github代码里，作者提供了预训练模型，所以分别采用学习率为0.0001和0.001的Adam优化算法来优化网络的特征提取器和分类器。
自己对于模型优化的看法：
这个模型比较老了，使用了dropout正则化的方式，可以将其替换成BN层。同时可以参考resnet结构，把时间和空间的维度分别拿出来进行卷积操作，如时间：3∗1∗1 + 空间：1∗3∗3。同时可以考虑光流，把光流也作为另一个模型的输入，将两个模型融合起来。