Staircases

  
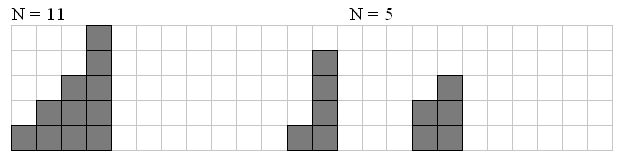
input
output
212
995645335
题意
这道题目要求计算给定数目的砖块可以组成多少种不同的楼梯。楼梯由不同高度的阶梯组成，不允许有两个阶梯有相同的高度。每个楼梯至少包含两个阶梯，每个阶梯至少包含一个砖块。
数学背景
这道题目涉及到数的分划，属于组合数学和数论的研究领域。
数 n 的分划(partition)是将 n 表示成任意多个正整数之和的形式。例如，数 5 的分划如下：
5 
4 + 1 
3 + 2 
3 + 1 + 1 
2 + 2 + 1 
2 + 1 + 1 + 1 
1 + 1 + 1 + 1 + 1 
用 p(n) 来记 n 的分划的个数，这样就有 p(5) = 7。
为了求解 p(n)，我们引入一个中间函数 p(k, n)，表示数 n 的最小被加数不小于 k 的分划的个数。对于给定的 k 值，p(k, n) 正好分为以下两类：
最小被加数等于 k
最小被加数大于 k
满足第一个条件的分划的个数是 p(k, n − k)。 这是因为，让我们想象数 n − k 的最小被加数不小于 k 的分划，然后将 "+ k" 附加每一个分划后面，就得到数 n 的最小被加数等于 k 的分划。以 n = 5, k = 1 为例，数 4 的最小被加数不小于 1 的分划是 4、3 + 1、2 + 2、2 + 1 + 1 和1 + 1 + 1 + 1，即 p(k, n − k) = p(1, 4) = 5。然后，将 "+ 1" 附加在这 5 个分划后面，就得到数 5 的最小被加数等于 1 的分划：4 + 1、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1 和 1 + 1 + 1 + 1 + 1。
满足第二个条件的分划的个数是 p(k + 1, n) 。以 n = 5, k = 1 为例，数 5 的最小被加数大于 1 的分划是 5 和 3 + 2，即 p(k + 1, n) =p(2, 5) = 2。
也就是说，p(1, 5) = p(2, 5) + p(1, 4)。因此：
p(k, n) = 0  如果 k > n 
p(k, n) = 1  如果 k = n 
p(k, n) = p(k+1, n) + p(k, n-k)  其它情况 
这样，就可以递归地求解 p(k, n)，其部分值见下表：
 
k
1
2
3
4
5
6
7
8
9
10
n
1
1
0
0
0
0
0
0
0
0
0
2
2
1
0
0
0
0
0
0
0
0
3
3
1
1
0
0
0
0
0
0
0
4
5
2
1
1
0
0
0
0
0
0
5
7
2
1
1
1
0
0
0
0
0
6
11
4
2
1
1
1
0
0
0
0
7
15
4
2
1
1
1
1
0
0
0
8
22
7
3
2
1
1
1
1
0
0
9
30
8
4
2
1
1
1
1
1
0
10
42
12
5
3
2
1
1
1
1
1

最后，p(n) = p(1, n)。
 
现在，让我们的来考虑 将 n 分成不相等的正整数之和的分划。例如，数 8 的分划如下：
8 
7 + 1 
6 + 2 
5 + 3 
5 + 2 + 1 
4 + 3 + 1 
用 q(n) 来记 n 的分划的个数，这样就有 q(8) = 6。
为了求解 q(n)，我们引入一个中间函数 q(k, n)，表示数 n 的最小被加数不小于 k 的分划的个数。对于给定的 k 值，q(k, n) 正好分为以下两类：
最小被加数等于 k
最小被加数大于 k
满足第一个条件的分划的个数是 q(k + 1, n − k)。 这是因为，让我们想象数 n − k 的最小被加数大于 k 的分划，然后将 "+ k" 附加每一个分划后面，就得到数 n 的最小被加数等于 k 的分划。以 n = 8, k = 1 为例，数 7 的最小被加数大于 1 的分划是 7、5 + 2 和 4 + 3，即 q(k + 1,n − k) = q(2, 7) = 3。然后，将 "+ 1" 附加在这 3 个分划后面，就得到数 8 的最小被加数等于 1 的分划：7 + 1、5 + 2 + 1 和 4 + 3 + 1。
满足第二个条件的分划的个数是 q(k + 1, n) 。以 n = 8, k = 1 为例，数 8 的最小被加数大于 1 的分划是 8、6 + 2 和 5 + 3，即 q(k + 1,n) = q(2, 8) = 3。
也就是说，q(1, 8) = q(2, 8) + q(2, 7)。因此：
q(k, n) = 0  如果 k > n 
q(k, n) = 1  如果 k = n 
q(k, n) = q(k+1, n) + q(k + 1, n-k)  其它情况 
这样，就可以递归地求解 q(k, n)，其部分值见下表：
 
k
1
2
3
4
5
6
7
8
9
10
n
1
1
0
0
0
0
0
0
0
0
0
2
1
1
0
0
0
0
0
0
0
0
3
2
1
1
0
0
0
0
0
0
0
4
2
1
1
1
0
0
0
0
0
0
5
3
2
1
1
1
0
0
0
0
0
6
4
2
1
1
1
1
0
0
0
0
7
5
3
2
1
1
1
1
0
0
0
8
6
3
2
1
1
1
1
1
0
0
9
8
5
3
2
1
1
1
1
1
0
10
10
5
3
2
1
1
1
1
1
1

最后，q(n) = q(1, n)。
解题思路
用 n 块砖块可以组成的楼梯的个数，就是将 n 分成不相等的正整数之和的分划的个数 q(n) 减一，因为每个楼梯至少包含两个阶梯。
 
 
妈蛋坑逼数学题。。。
代码如下
#include<stdio.h>
double f[501][501];
int main(){
long n,q,i,j;
for (i=1;i<=500;++i)
for (j=1;j<=500;++j){
if (i==j) f[i][j]=1;
else f[i][j]=0;
}
for(i=1;i<=500;++i)
for(j=i-1;j>=1;--j)
f[i][j]=f[i][j+1]+f[i-j][j+1];
while (scanf("%d",&n)!=EOF && n!=0)
printf("%.0lf\n",f[n][1]-1);
}