文章目录
- 一、概述
- 二、参数估计——区间估计
- 三、经验分布函数
- 1.定义
- 2.头颅宽度(经验分布函数计算与绘图)
- 四、Q-Q图(直观检验拟合优度)
- 1.介绍
- 2.基本思想
- 3.计算步骤
- 4.Q-Q图绘图(仍然以头颅宽度为例)
- 五、 χ 2 {\chi}^2 χ2拟合优度检验(量化检验拟合优度)
- 1.给出的假设(可含未知参数)
- 2.检验步骤
- 3.书页印刷(检验是否与泊松分布拟合,离散)
- 4.灯泡寿命(检验是否与指数分布拟合,连续)
- 5.成绩统计(检验是否与正态分布拟合,连续)
- 六、柯尔莫哥洛夫检验
- 1.介绍(与 χ 2 \chi^{2} χ2检验的比较)
- 2.步骤
- 3.头颅宽度(检验是否服从正态分布)
- 七、秩和检验
- 1.目的
- 2.步骤
- 3.涂漆温度
- 七、Bootstrap
- 1.非参数Bootstrap方法
- (一)介绍
- (二)估计量的标准误差的Bootstrap估计——介绍与思想
- (三)估计量的标准误差的Bootstrap估计——基本步骤
- (四)估计量的标准误差的Bootstrap估计——基金回报
- (五)估计量的均方误差的Bootstrap估计——思想方法
- (六)估计量的均方误差的Bootstrap估计——金属升华
- (七)求未知参数 θ \theta θ的Bootstrap置信区间——思想方法
- (八)求未知参数 θ \theta θ的Bootstrap置信区间——仔猪存活
- 2.参数Bootstrap方法
- (一)介绍
- (二)电子元件(求最大似然估计和单侧置信下限)
- (三)血型分布(求最大似然估计和置信区间)
- 八、方差分析(单因素实验)
- 1.背景
- 2.假设前提
- 3.待检假设 H 0 : μ 1 = μ 2 = … = μ s = μ H_0:\mu_1=\mu_2=…=\mu_s=\mu H0:μ1=μ2=…=μs=μ
- 4.检验方法
- 5.产量差异(差异显著度)
- 九、回归分析
- 1.多元线性回归
- (一)模型
- (二)参数估计
- (三)统计分析
- (四)回归模型的假设检验
- (五)回归系数的假设检验和区间估计
- (六)利用回归模型进行预测
- 2.多元二项式回归
- (一) r s t o o l rstool rstool工具介绍
- (二)模型类型
- (三)个体性状
- 3.非线性回归
- (一)介绍
- (二)化学反应(拟合回归系数以及其置信区间、预测值及其置信空间)
- 4.血压与年龄、体重指数、吸烟习惯(建立回归模型)
- (一)问题背景
- (二)模型建立
- (三)模型求解( M A T L A B MATLAB MATLAB计算)
- 5.软件开发人员的薪金(薪金与资历、管理责任、教育程度)
- (一)问题背景
- (二)模型建立(多元线性回归模型)
- (三)模型求解
- (四)结果分析(残差分析方法)
- (五)增加管理与教育的交互项
- (六)模型应用
- 6.投资额与国民生产总值和物价指数(预测)
- (一)问题背景
- (二)问题分析
- (三)基本模型建立(多元线性)
- (四)基本回归模型结果分析( M A T L A B MATLAB MATLAB求解)
- (五)自相关性——定性诊断(残差诊断法)
- (六)自相关性——定量诊断(D-W检验)
- (七)自相关性——消除(广义差分法)
- (八)新模型的建立
- (九)两种模型的比较
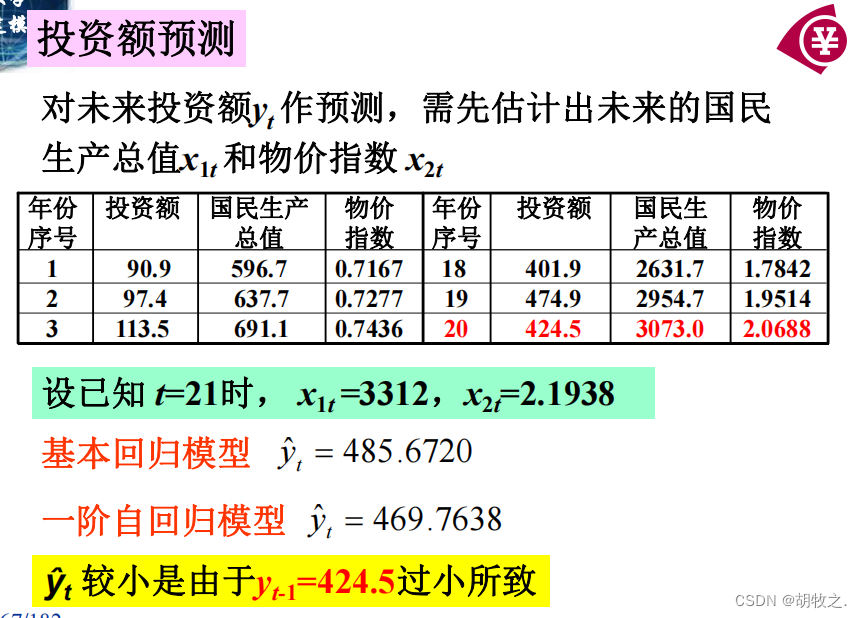
- (十)投资额预测
一、概述

二、参数估计——区间估计
1.糖果称重(求总体均值 μ \mu μ的双侧置信区间)


(一)根据公式计算结果


(二)直接使用 t t e s t ( ) ttest() ttest()函数

2.灯泡寿命( μ \mu μ的单侧置信区间)

程序运行:
>> a=[1050 1100 1120 1250 1280]a =1 至 4 列1050 1100 1120 12505 列1280>> alpha=0.05;
>> mu=mean(a),sig=std(a),n=length(a);mu =1160sig =99.7497>> t=mu-sig/sqrt(n)*tinv(1-alpha,n-1)t =1.0649e+03>>
3.小球测定引力常数( μ \mu μ、 σ 2 {\sigma}^2 σ2的置信区间)




以金球为例,程序运行:
>> a=[6.683 6.681 6.676 6.678 6.679 6.672]a =1 至 4 列6.6830 6.6810 6.6760 6.67805 至 6 列6.6790 6.6720>> [h1,p1,ci1,st1]=ttest(a,mean(a),'Alpha',0.1)h1 =0p1 =1ci1 =6.6750 6.6813st1 = tstat: 0df: 5sd: 0.0039>> [h1,p1,ci1,st1]=vartest(a,var(a),'Alpha',0.1)h1 =0p1 =0.8318ci1 =1.0e-04 *0.0676 0.6533st1 = chisqstat: 5df: 5>>
三、经验分布函数
1.定义



2.头颅宽度(经验分布函数计算与绘图)


//参数解释(待补充……)
四、Q-Q图(直观检验拟合优度)
1.介绍

2.基本思想

3.计算步骤

4.Q-Q图绘图(仍然以头颅宽度为例)



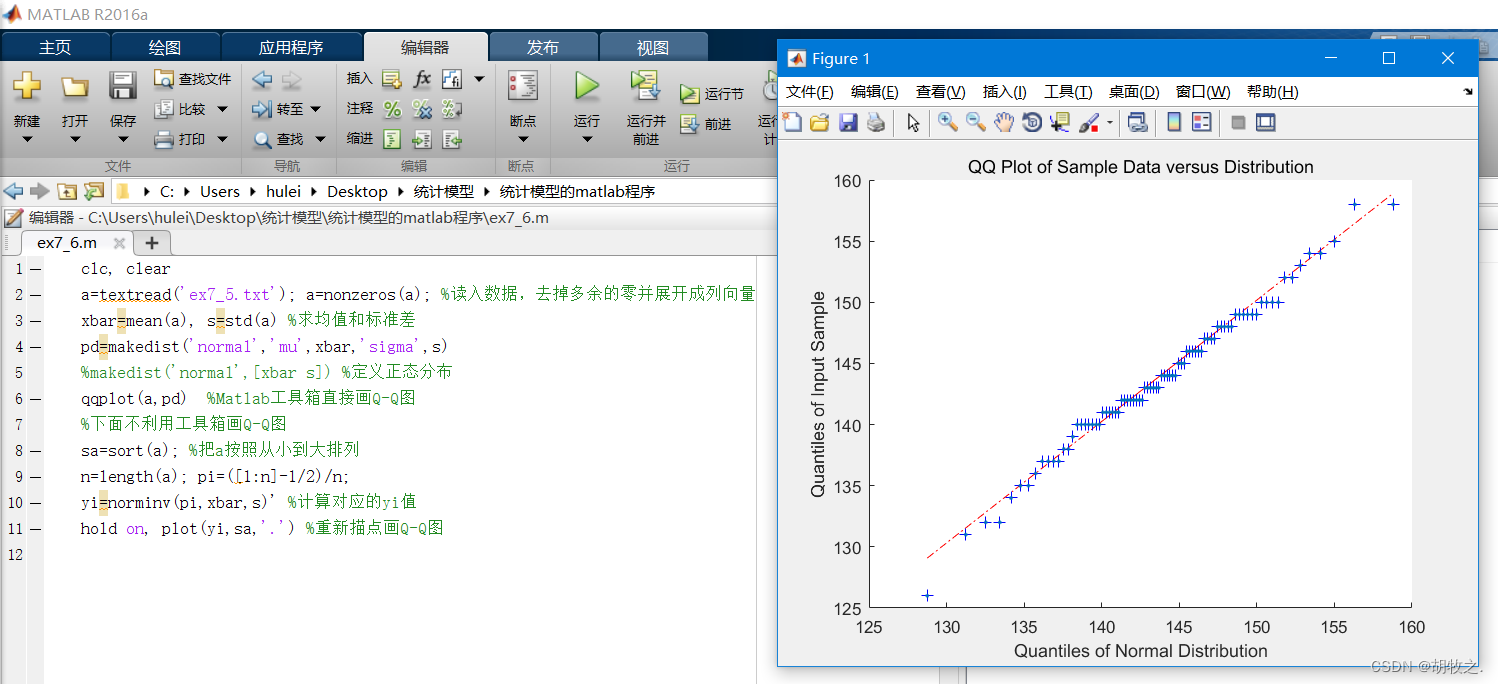
//参数解释待补充,特别注意那个 s s s
五、 χ 2 {\chi}^2 χ2拟合优度检验(量化检验拟合优度)
1.给出的假设(可含未知参数)

2.检验步骤
k:区间数
r:分布函数中未知参数的个数


3.书页印刷(检验是否与泊松分布拟合,离散)
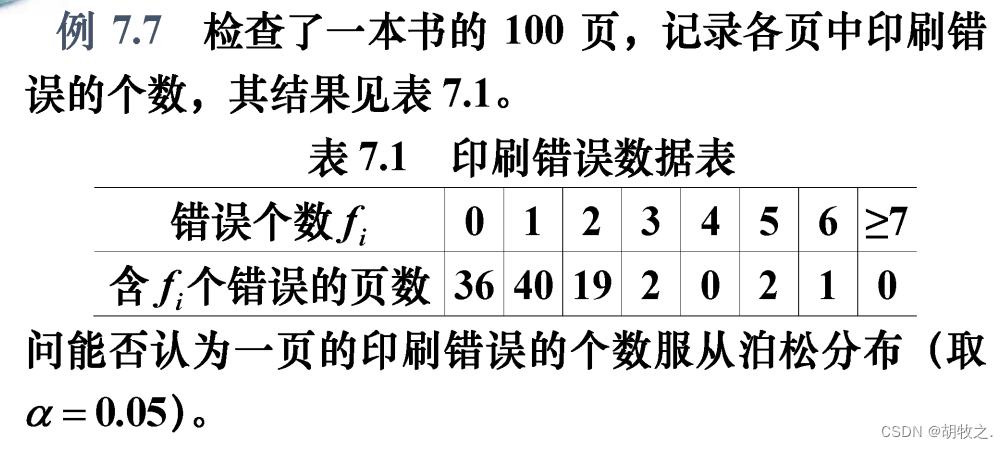


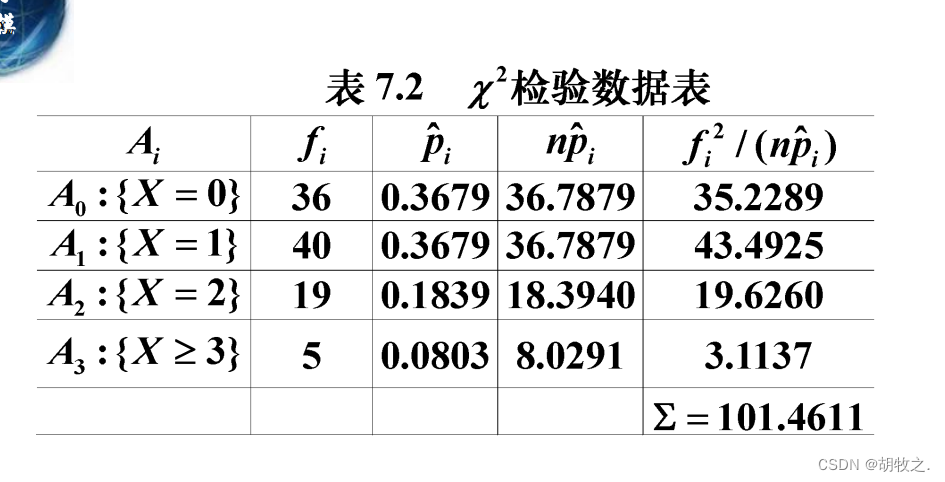


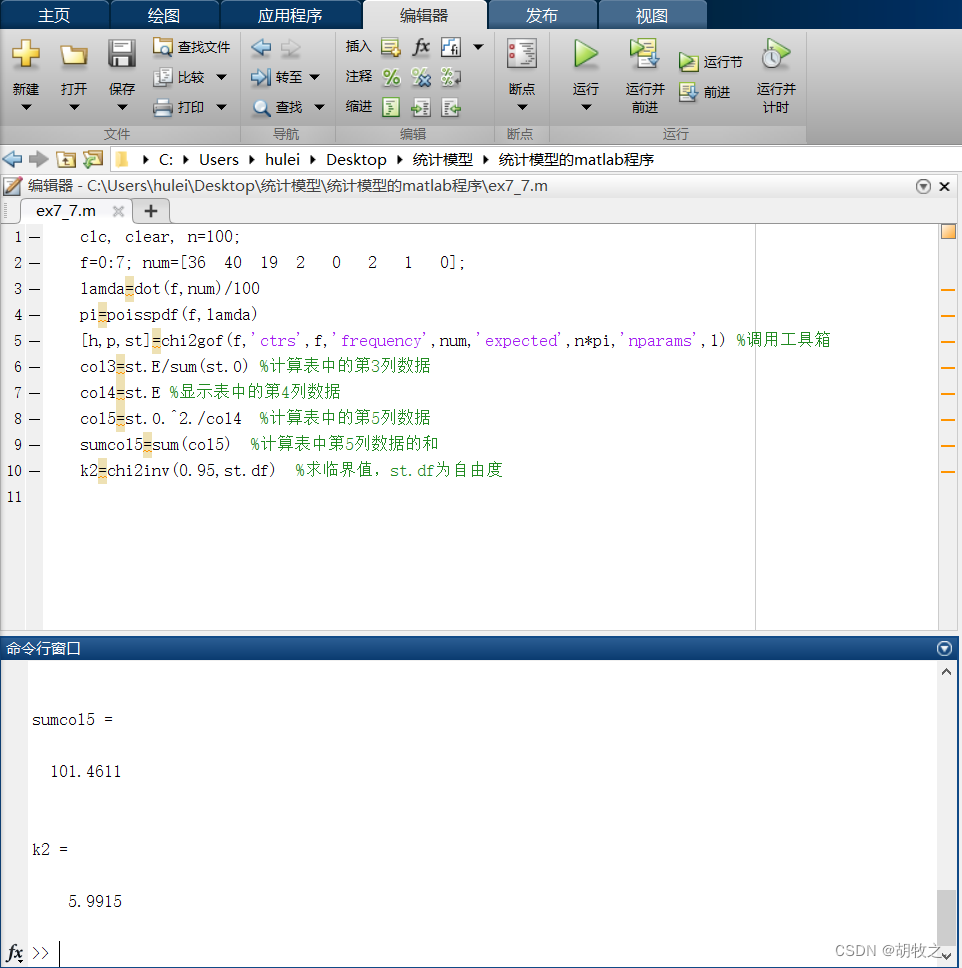
4.灯泡寿命(检验是否与指数分布拟合,连续)


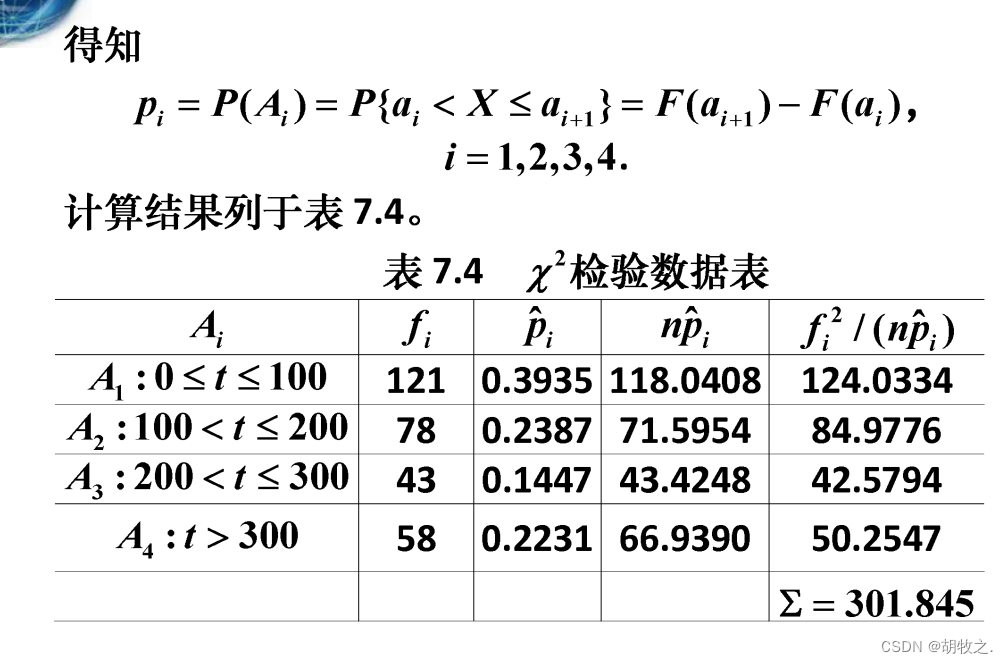

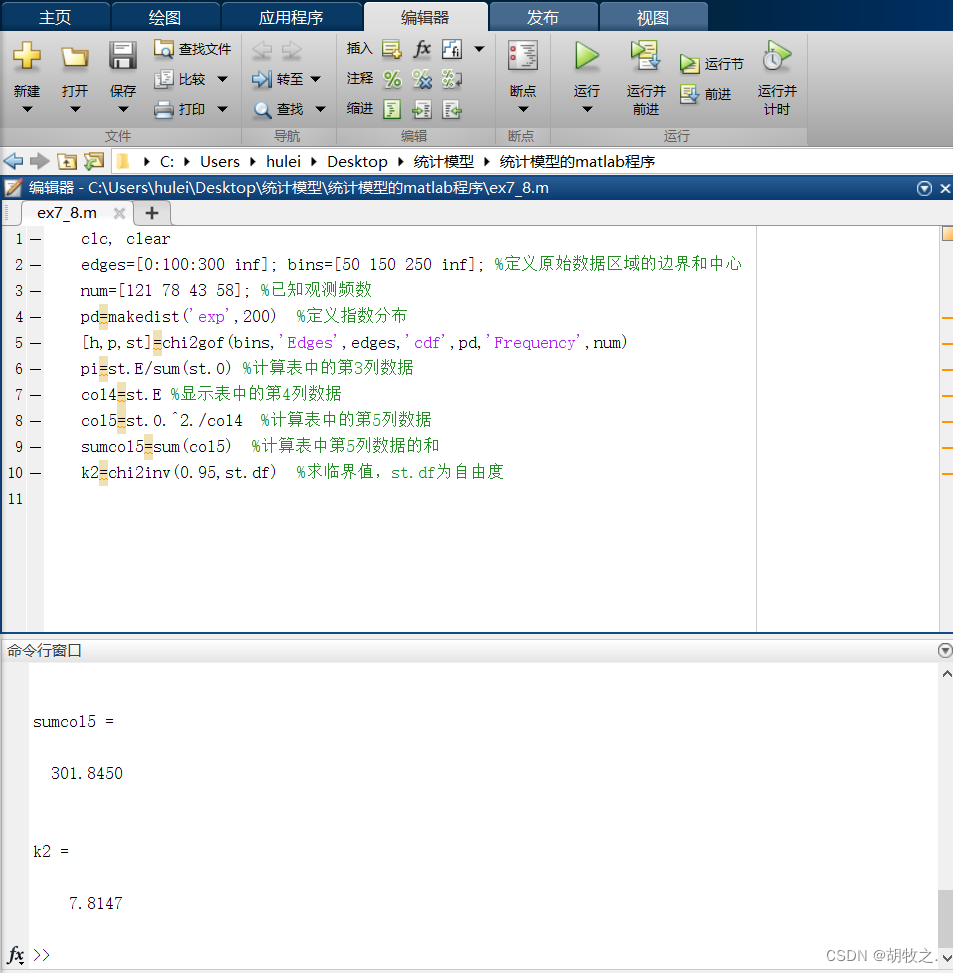
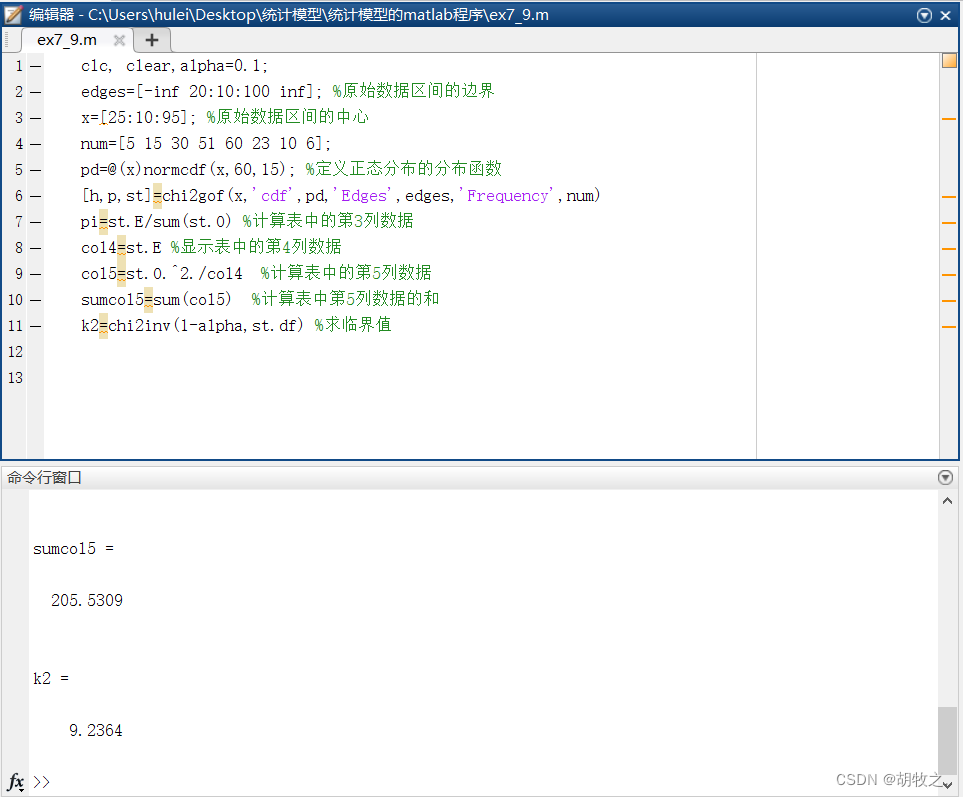
5.成绩统计(检验是否与正态分布拟合,连续)
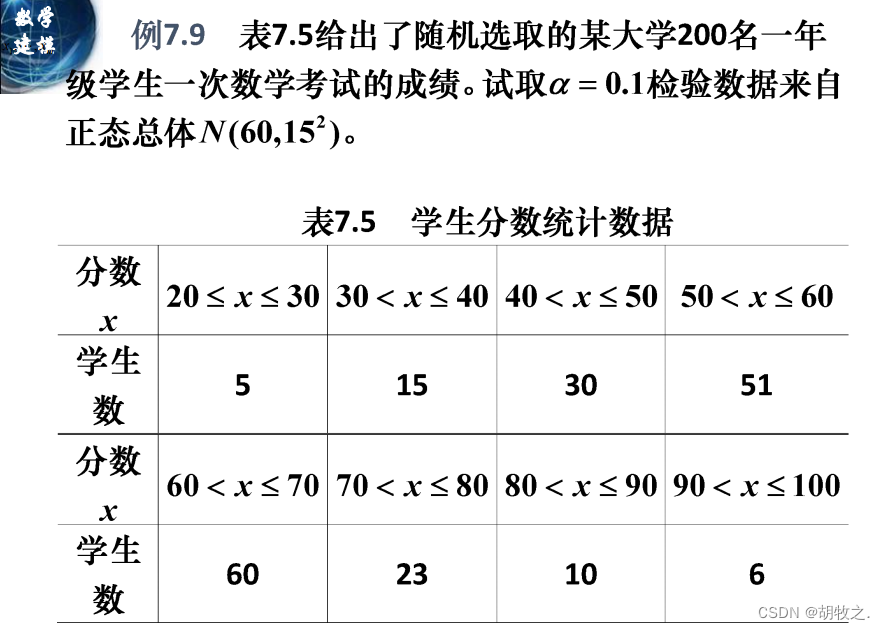


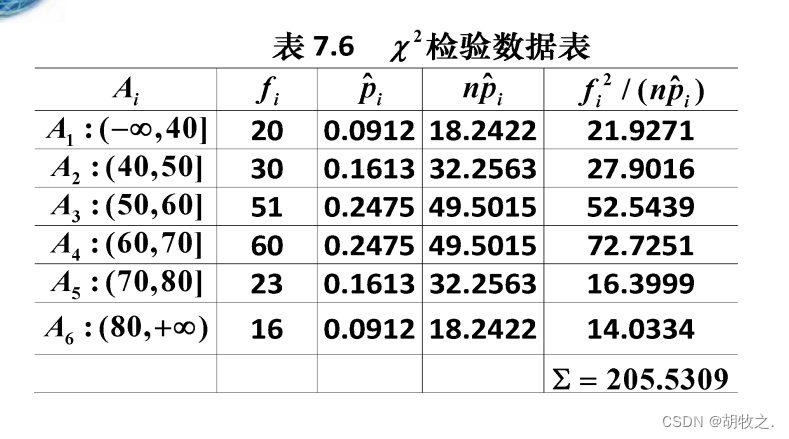
样本总数为200, 205.5309 − 200 = 5.5309 < 9.2364 205.5309-200=5.5309<9.2364 205.5309−200=5.5309<9.2364
所以接受假设
六、柯尔莫哥洛夫检验
1.介绍(与 χ 2 \chi^{2} χ2检验的比较)



2.步骤
s u p — — s u p r e m u m — — sup——supremum—— sup——supremum——上确界




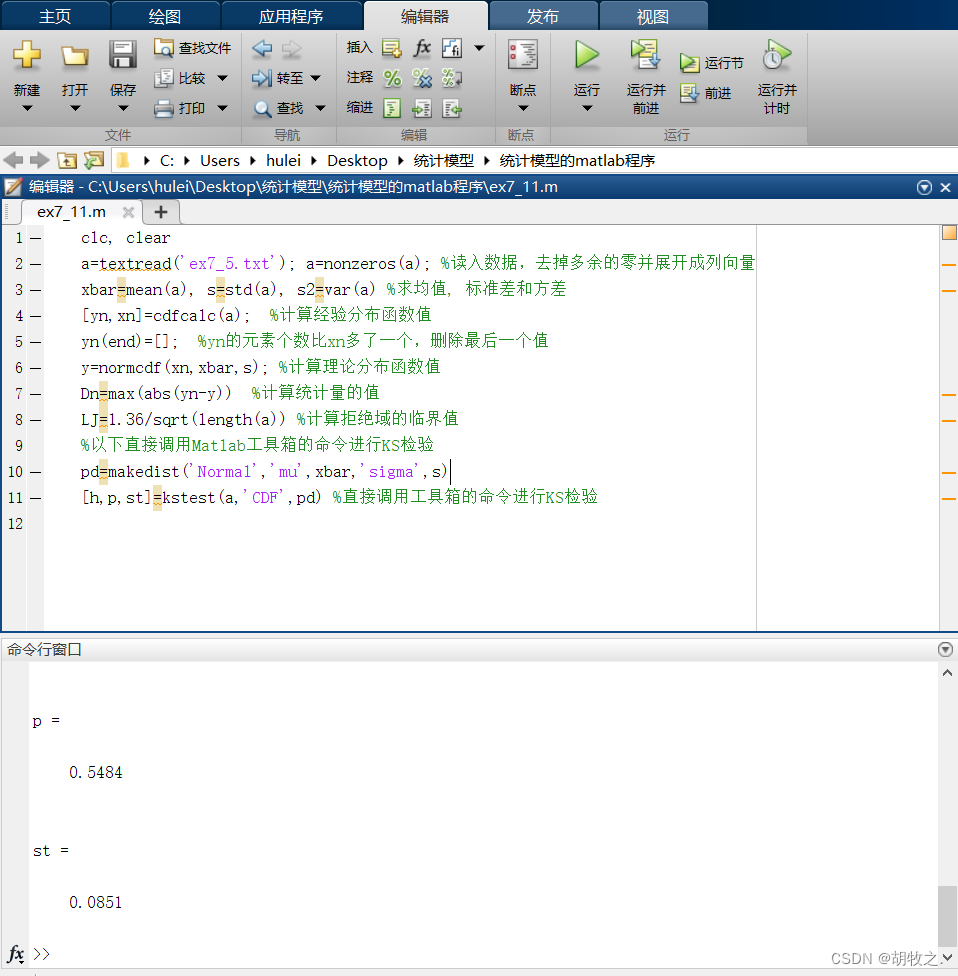
3.头颅宽度(检验是否服从正态分布)
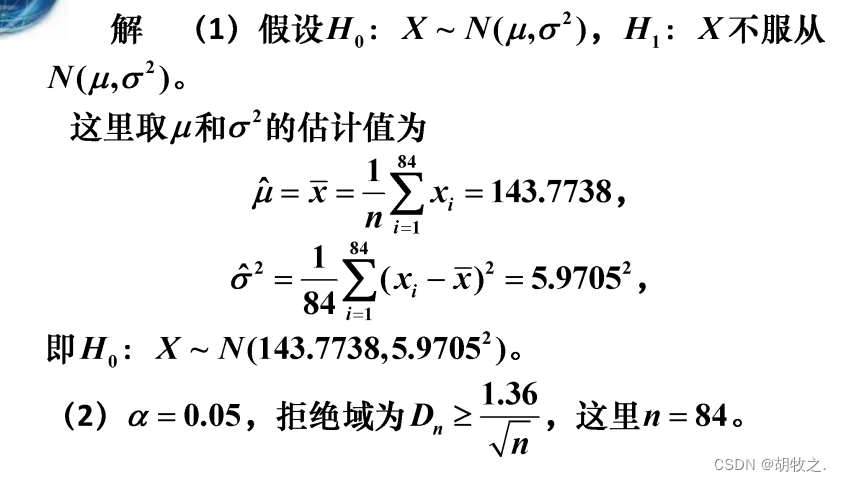

可调用工具箱实现 K S KS KS检验
七、秩和检验
1.目的


2.步骤


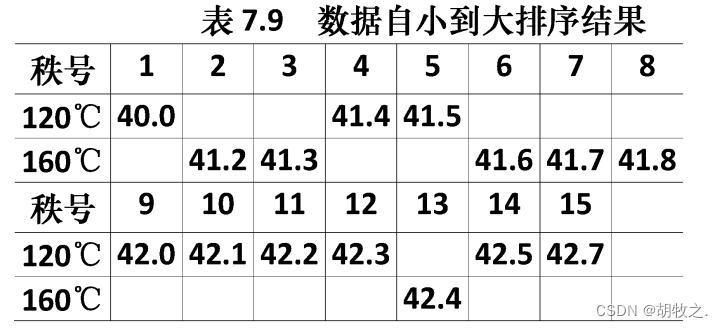
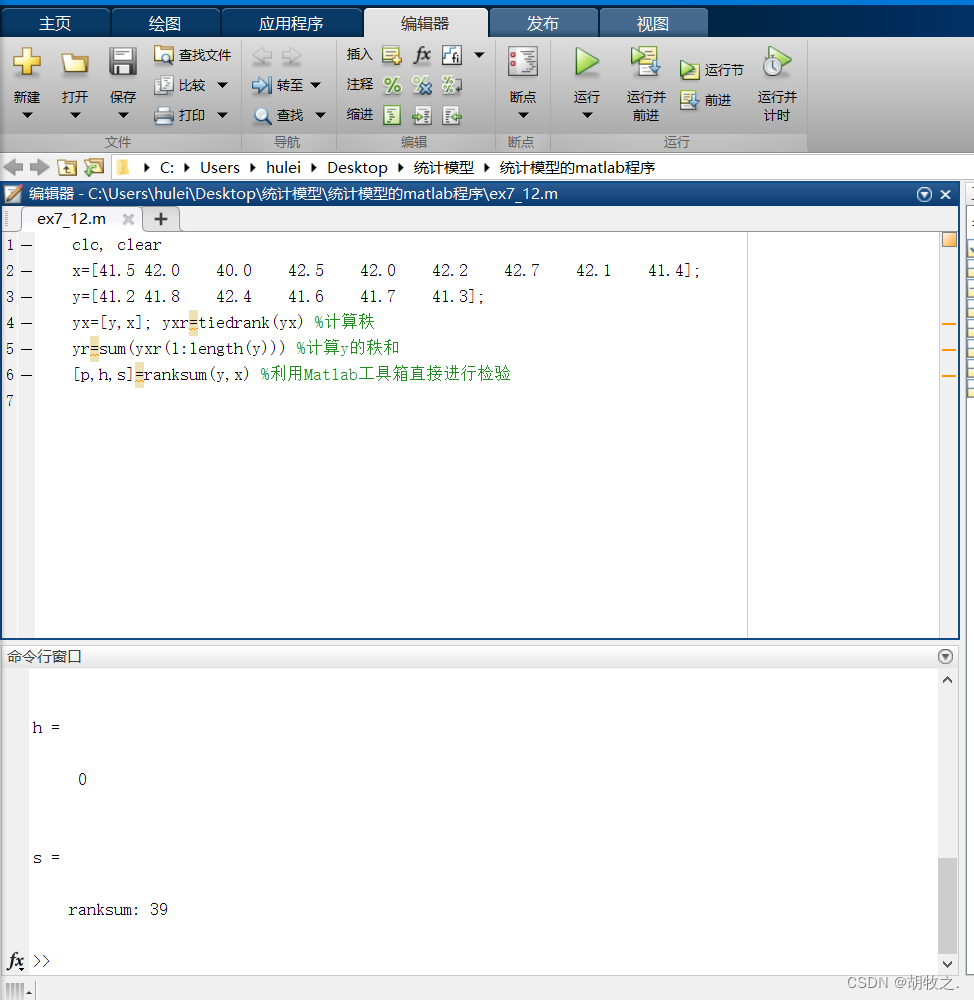
3.涂漆温度




七、Bootstrap
1.非参数Bootstrap方法
(一)介绍
独立地从原始样本中取多个Bootstrap样本


(二)估计量的标准误差的Bootstrap估计——介绍与思想






(三)估计量的标准误差的Bootstrap估计——基本步骤

(四)估计量的标准误差的Bootstrap估计——基金回报





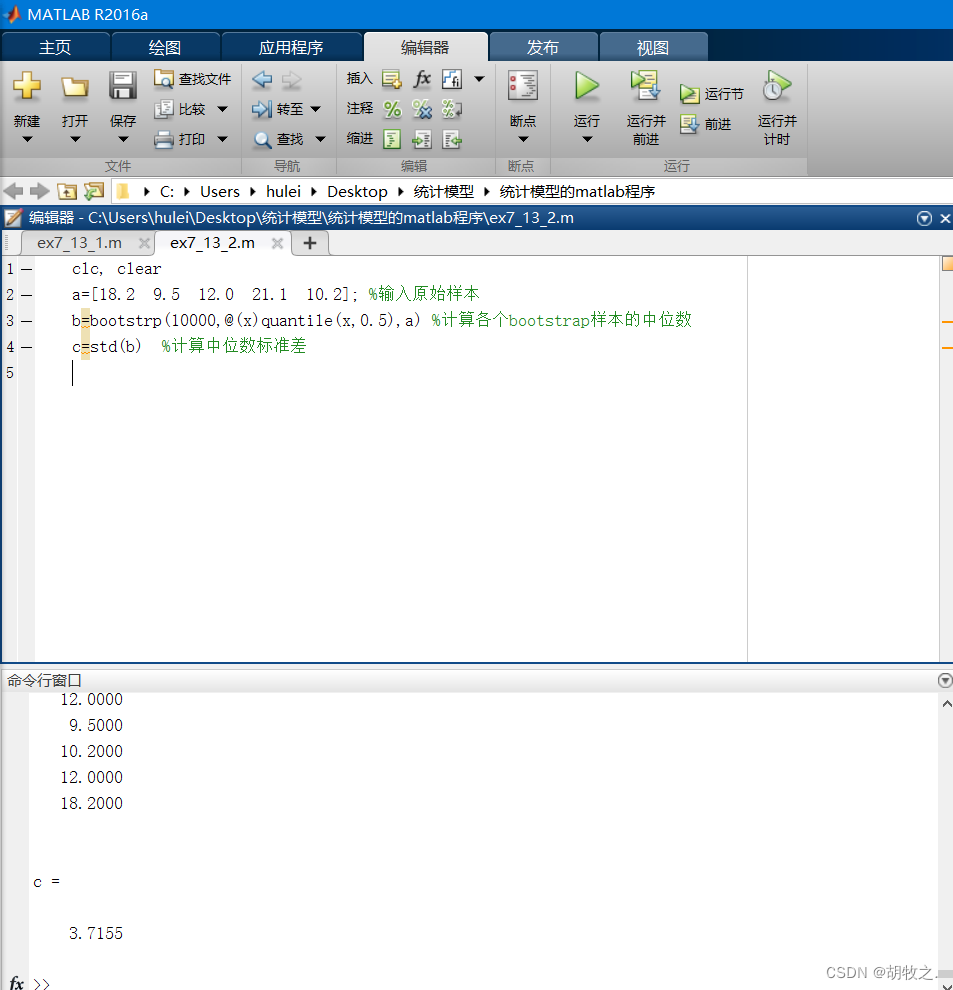
(五)估计量的均方误差的Bootstrap估计——思想方法
估计量的标准误差的步骤:

估计量的均方误差的步骤的区别:

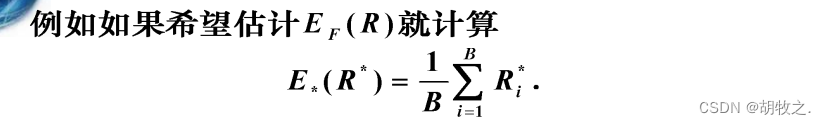
(六)估计量的均方误差的Bootstrap估计——金属升华




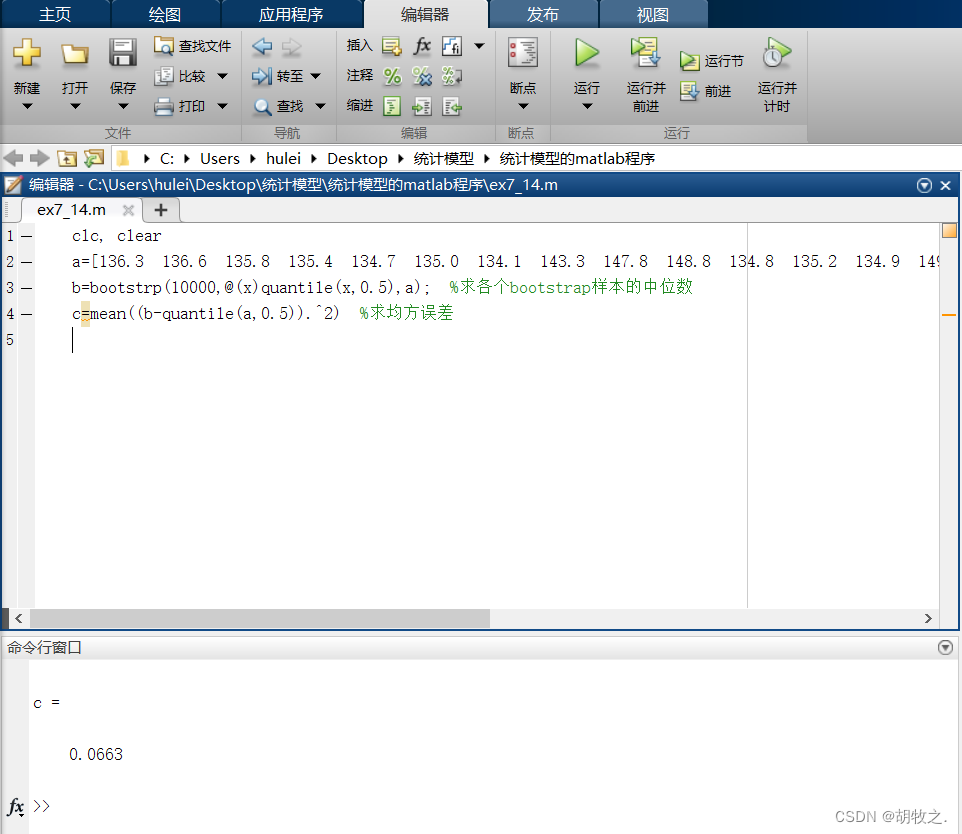
(七)求未知参数 θ \theta θ的Bootstrap置信区间——思想方法

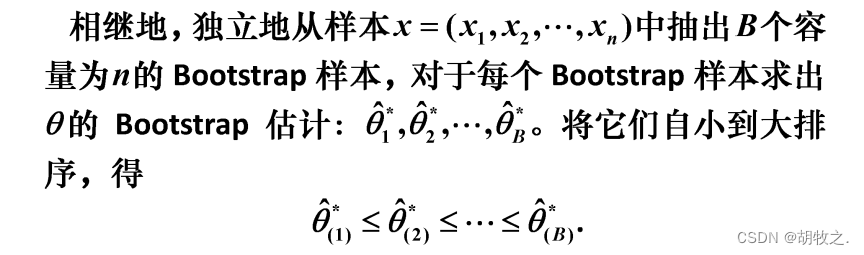
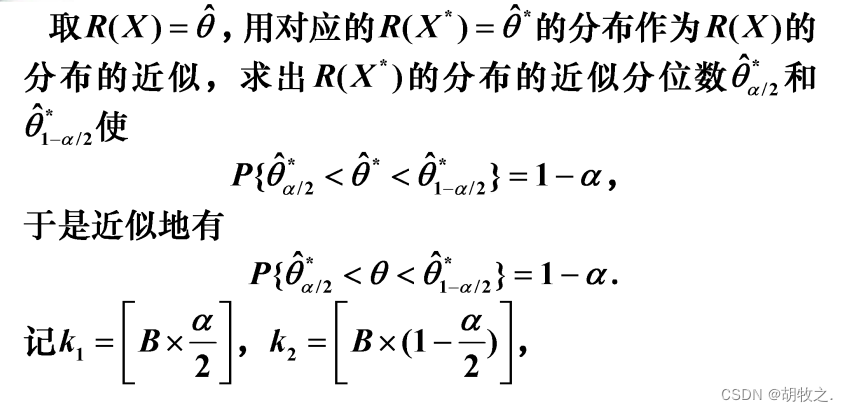

(八)求未知参数 θ \theta θ的Bootstrap置信区间——仔猪存活



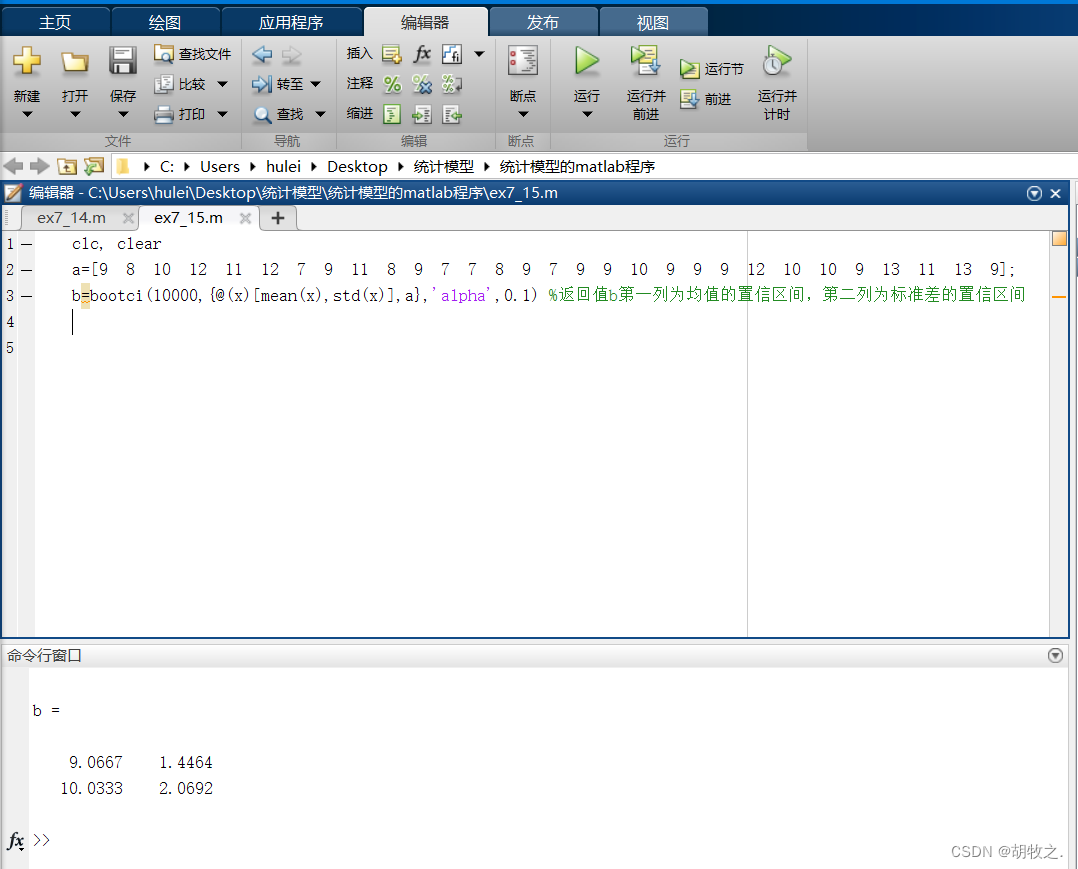

2.参数Bootstrap方法
(一)介绍


(二)电子元件(求最大似然估计和单侧置信下限)



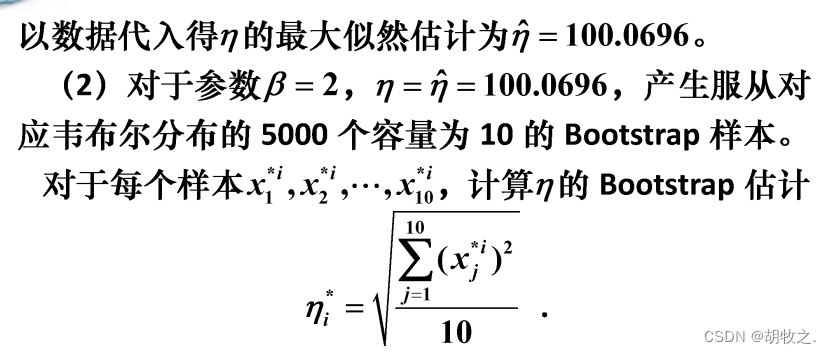

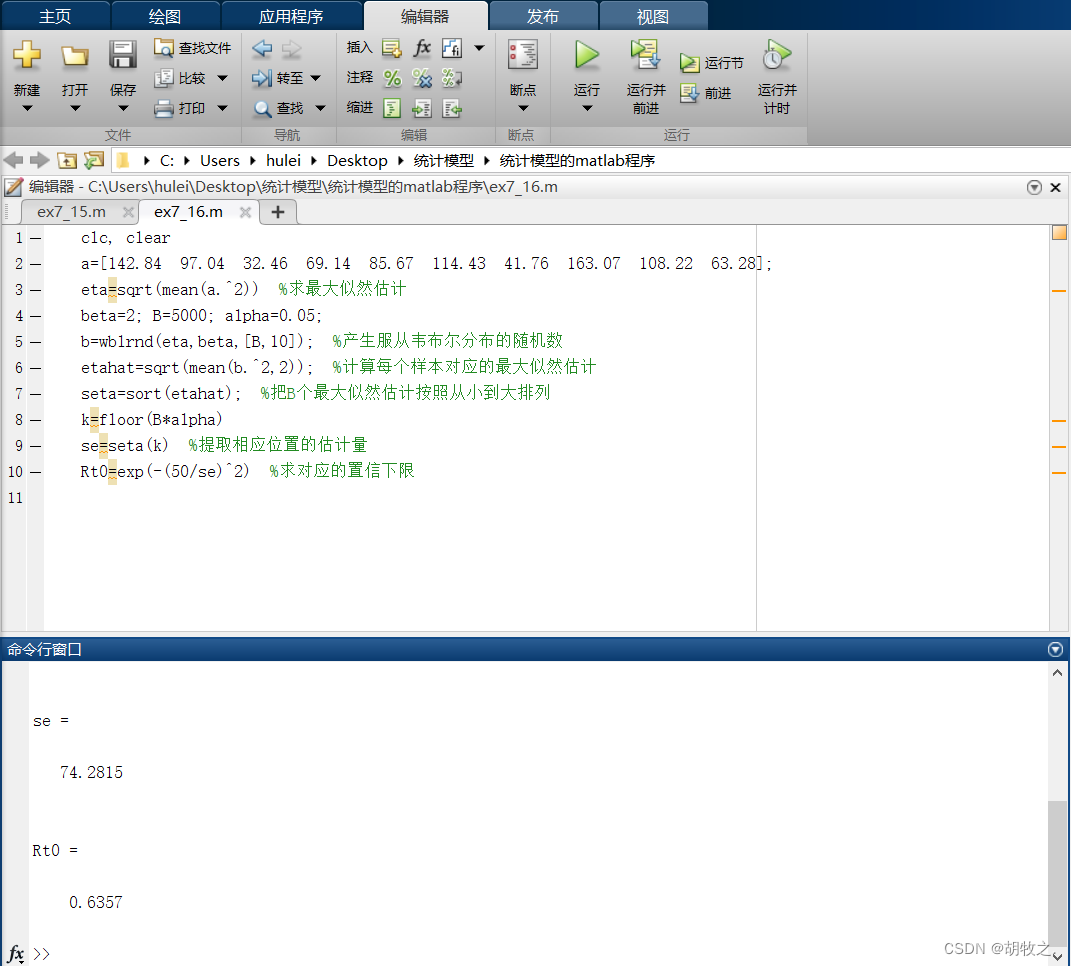
(三)血型分布(求最大似然估计和置信区间)
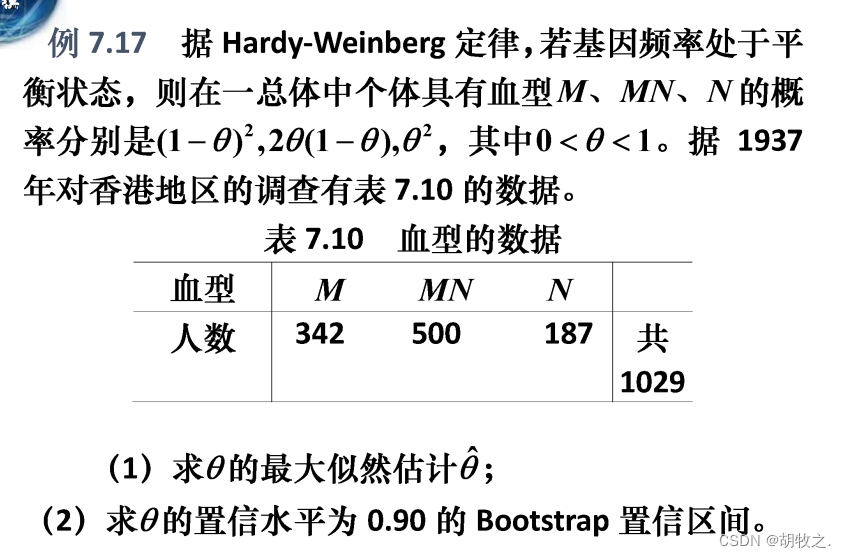



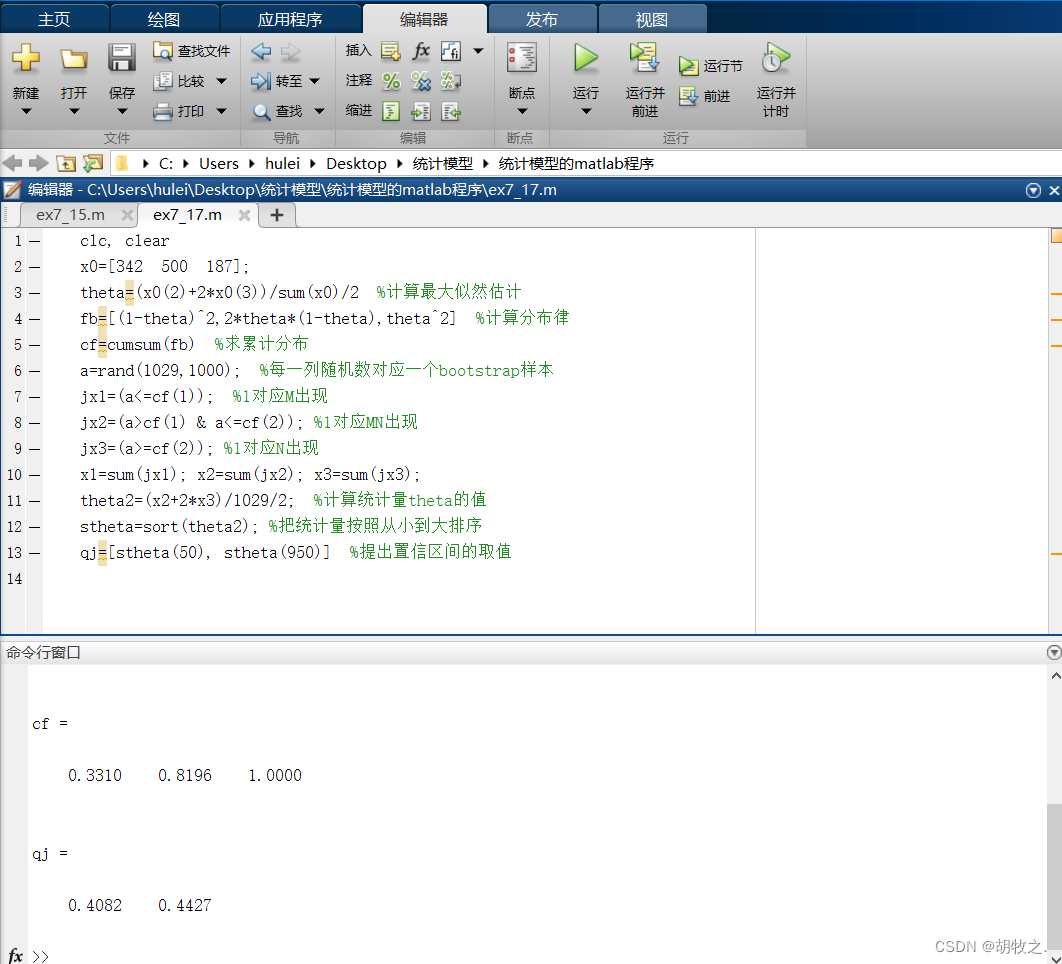
八、方差分析(单因素实验)
1.背景


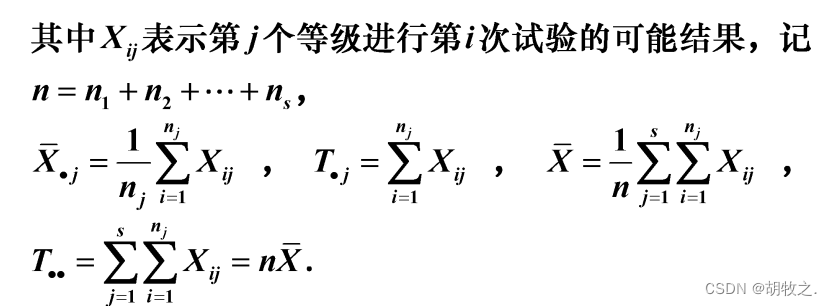
2.假设前提

3.待检假设 H 0 : μ 1 = μ 2 = … = μ s = μ H_0:\mu_1=\mu_2=…=\mu_s=\mu H0:μ1=μ2=…=μs=μ
4.检验方法
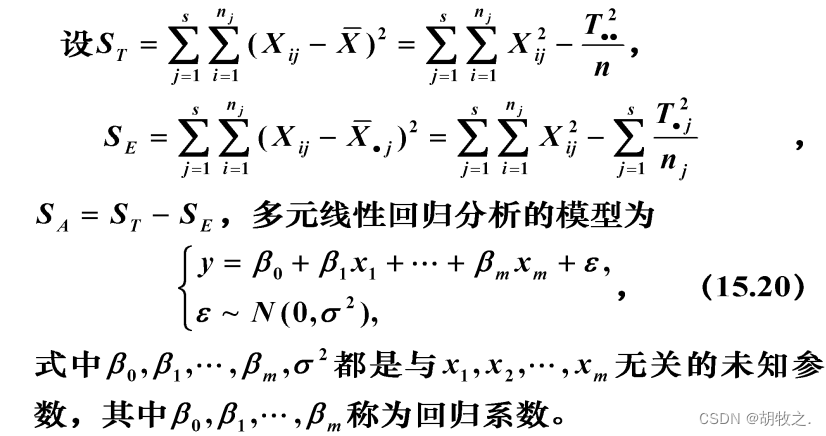

5.产量差异(差异显著度)
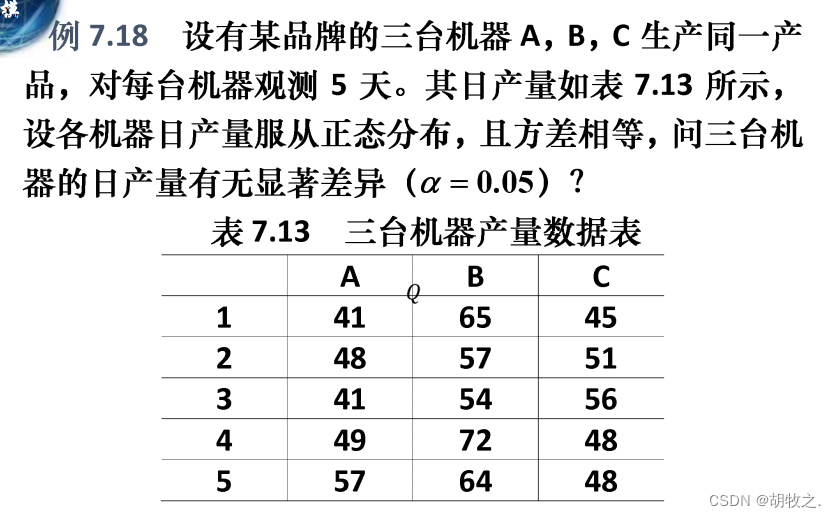

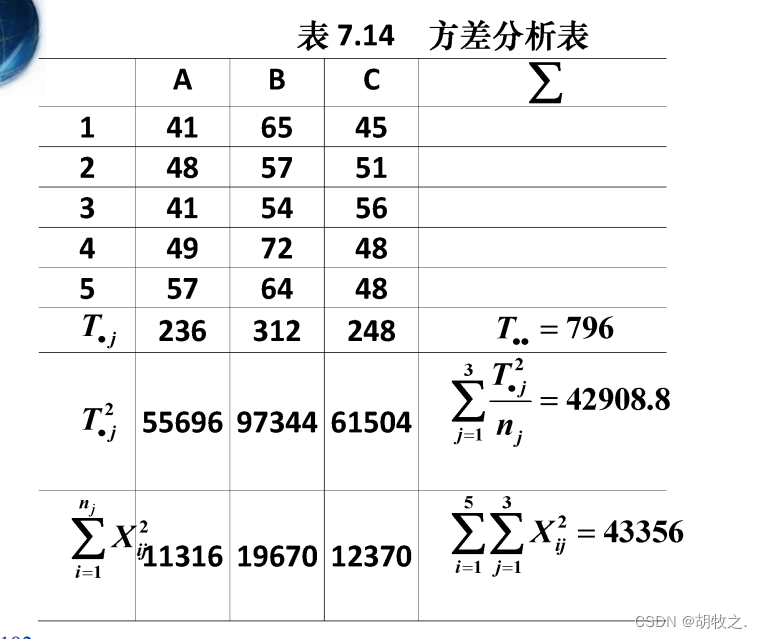

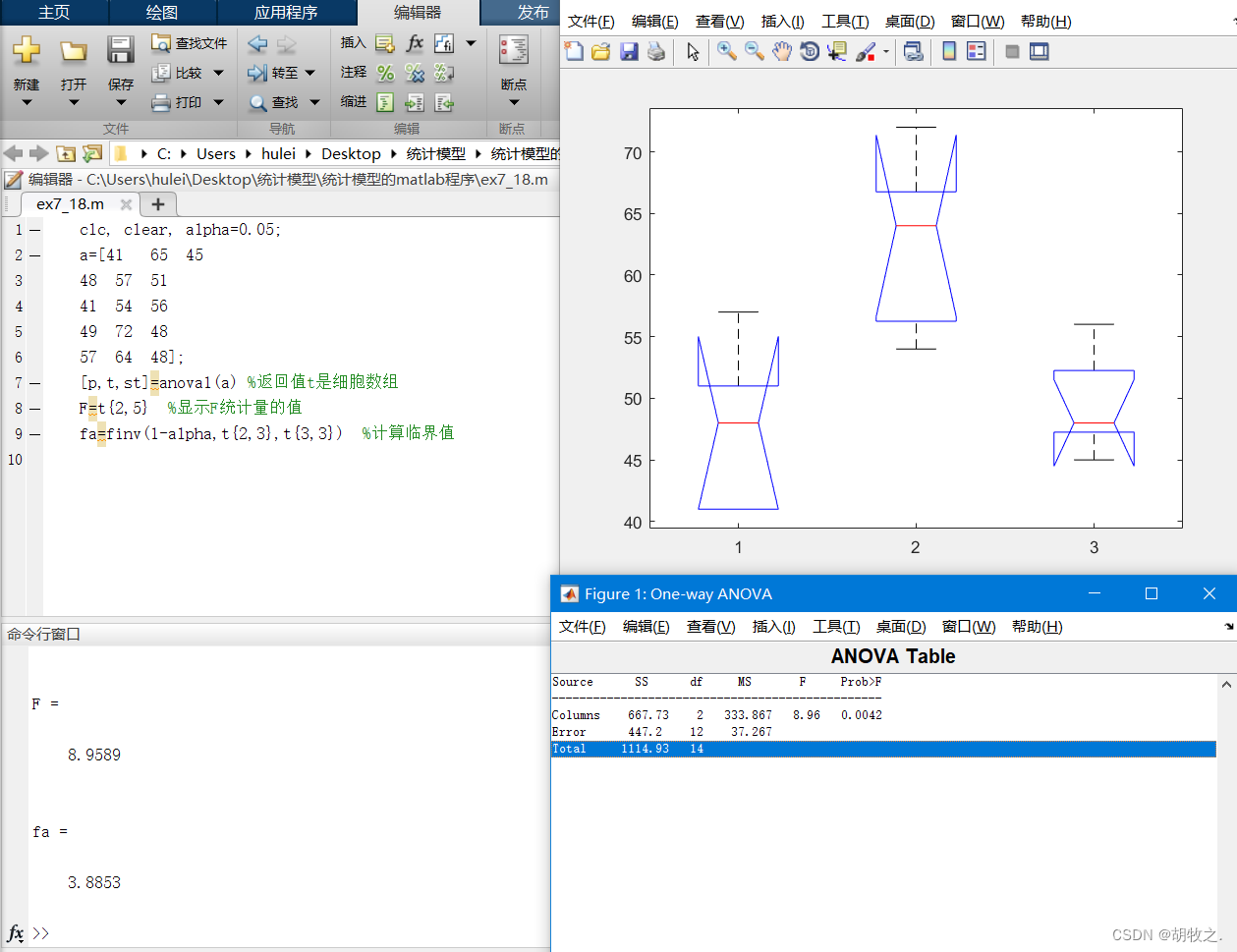
九、回归分析
1.多元线性回归
(一)模型


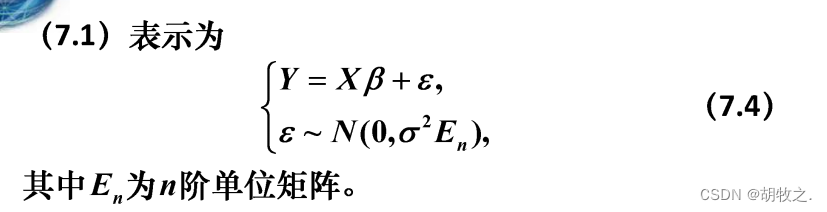
(二)参数估计
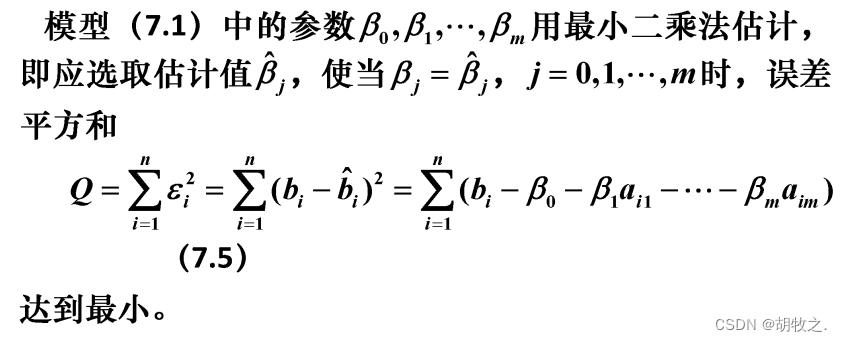
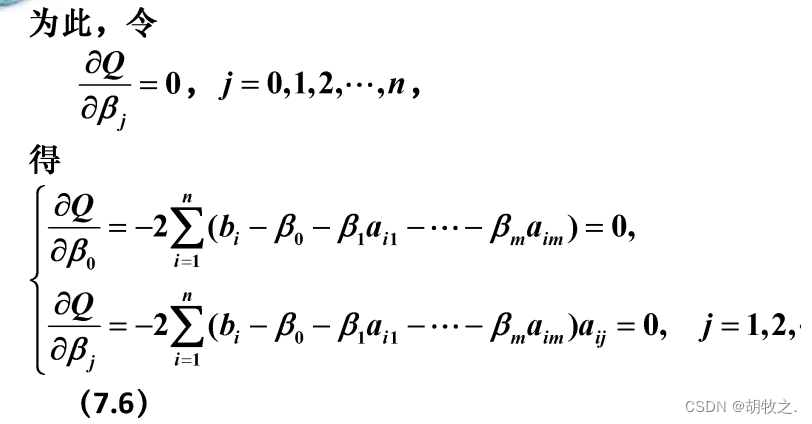


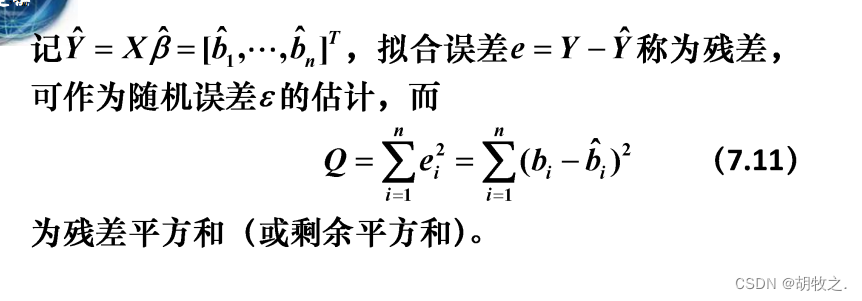
(三)统计分析



(四)回归模型的假设检验



(五)回归系数的假设检验和区间估计


(六)利用回归模型进行预测


2.多元二项式回归
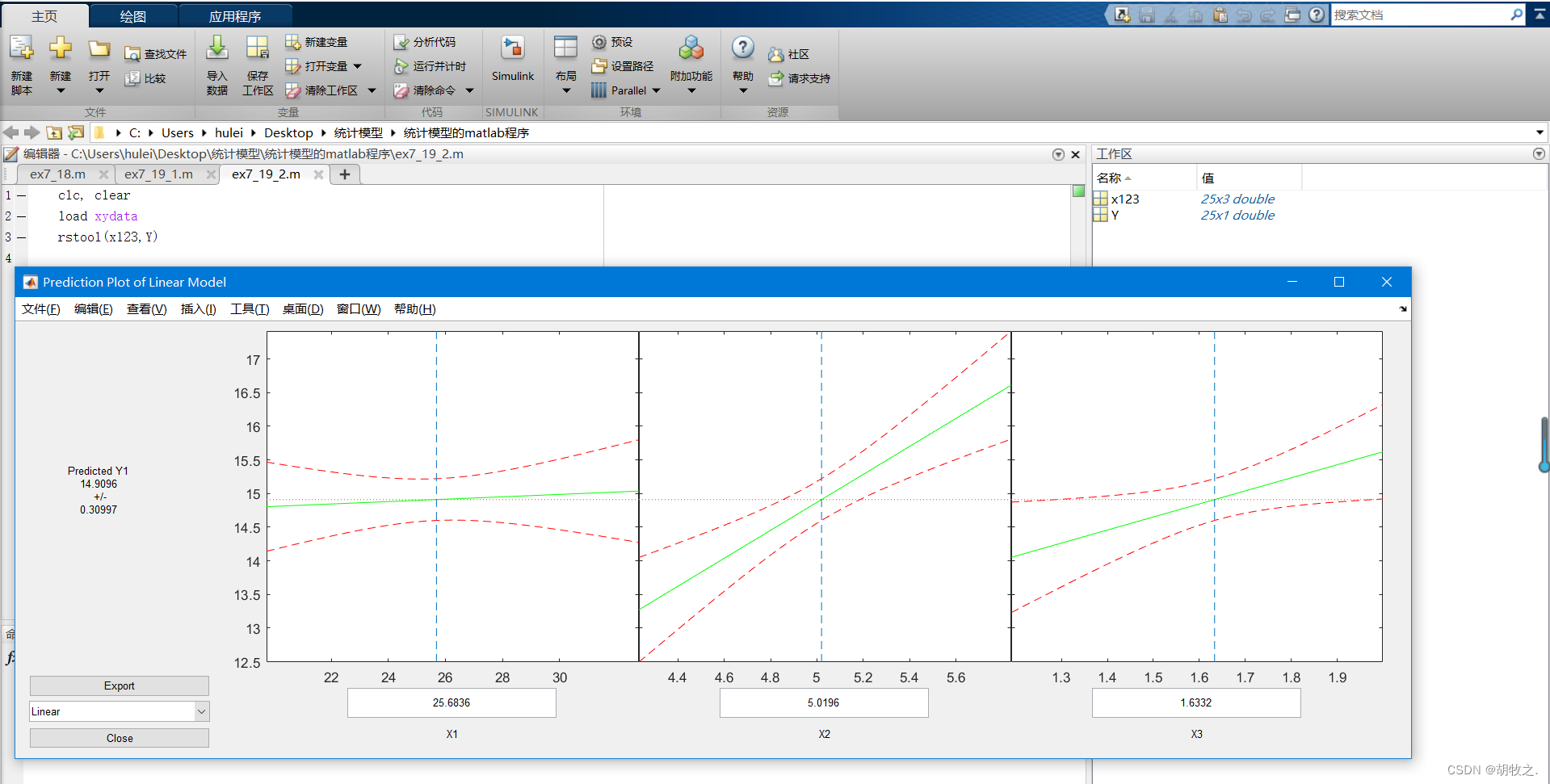
(一) r s t o o l rstool rstool工具介绍

(二)模型类型



(三)个体性状



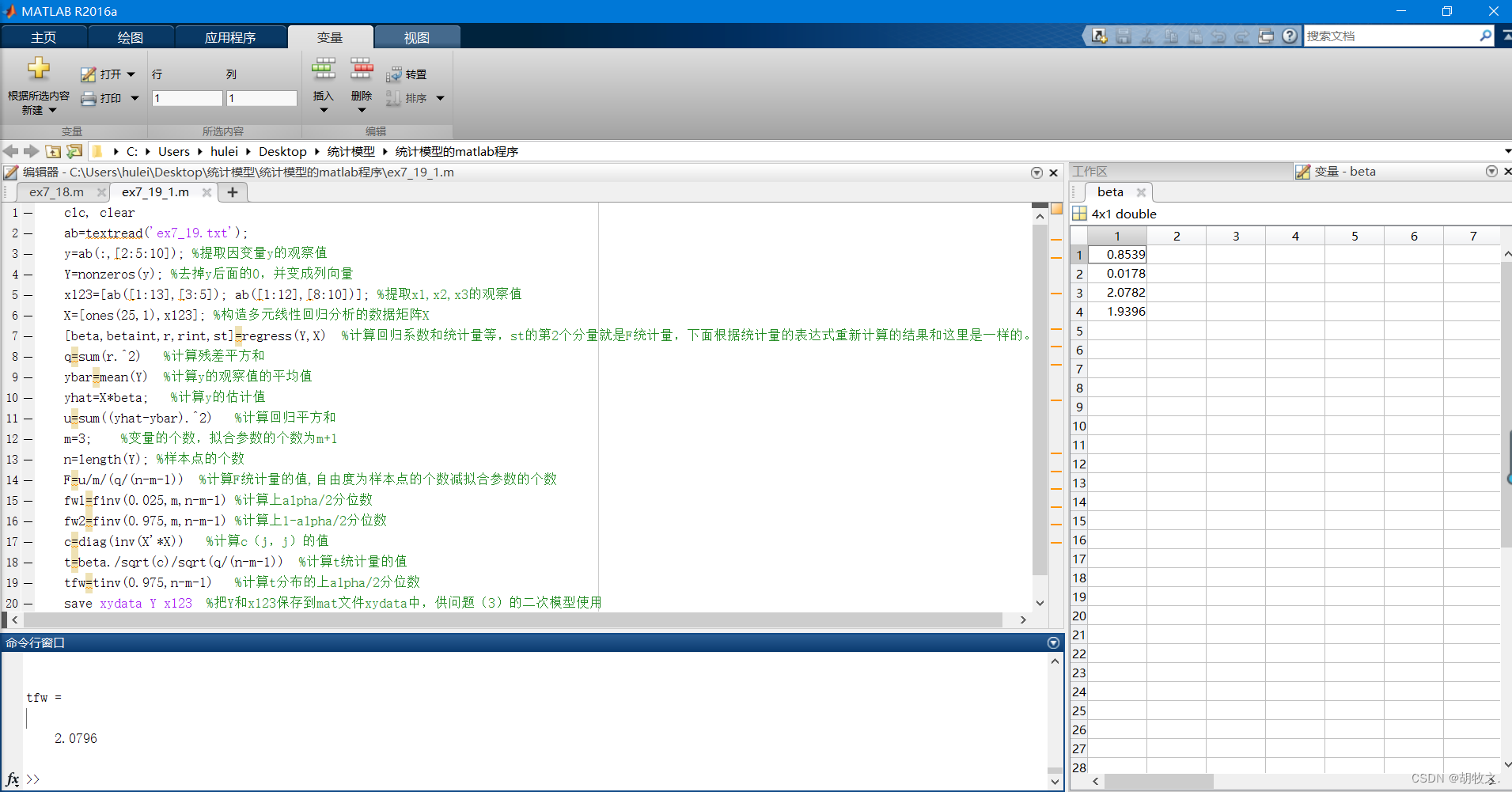







3.非线性回归
(一)介绍

(二)化学反应(拟合回归系数以及其置信区间、预测值及其置信空间)

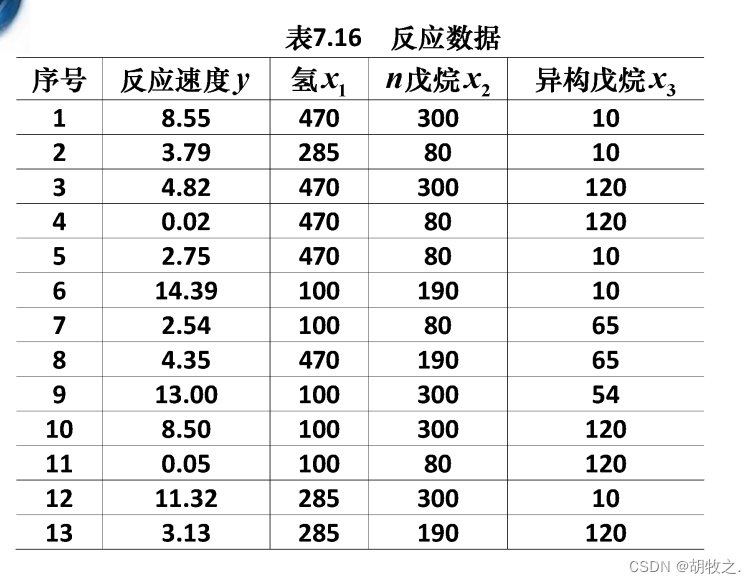


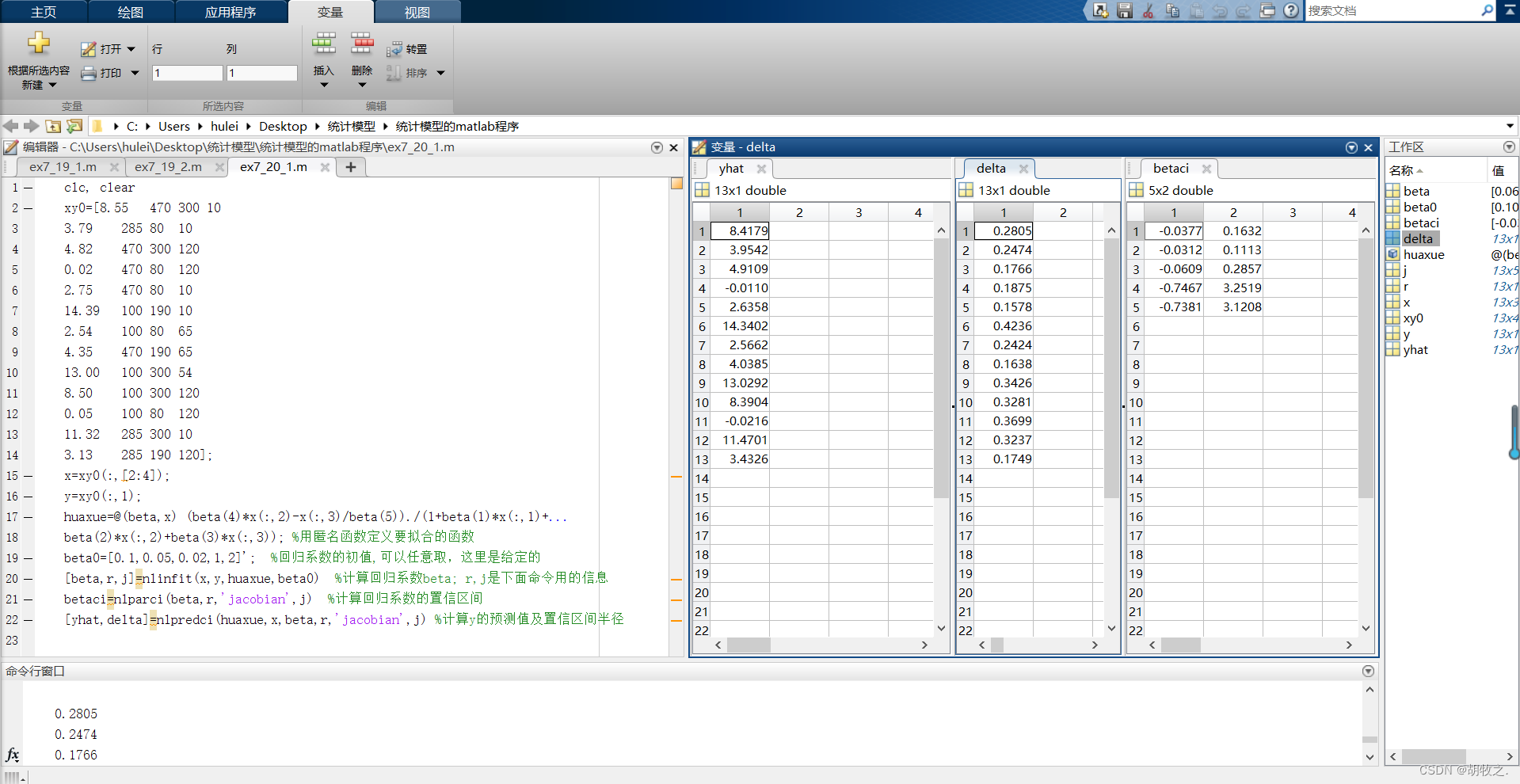
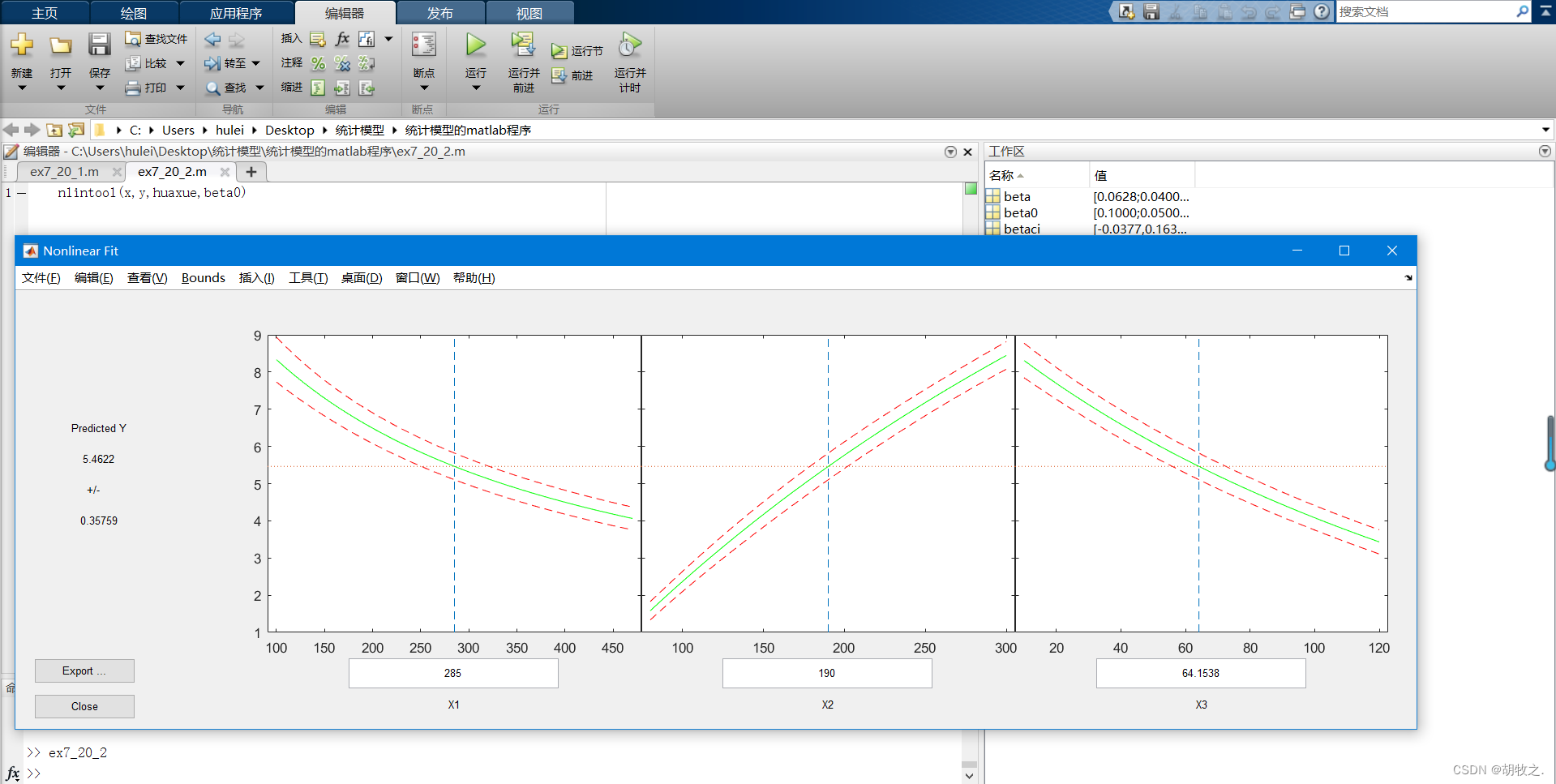
4.血压与年龄、体重指数、吸烟习惯(建立回归模型)
(一)问题背景
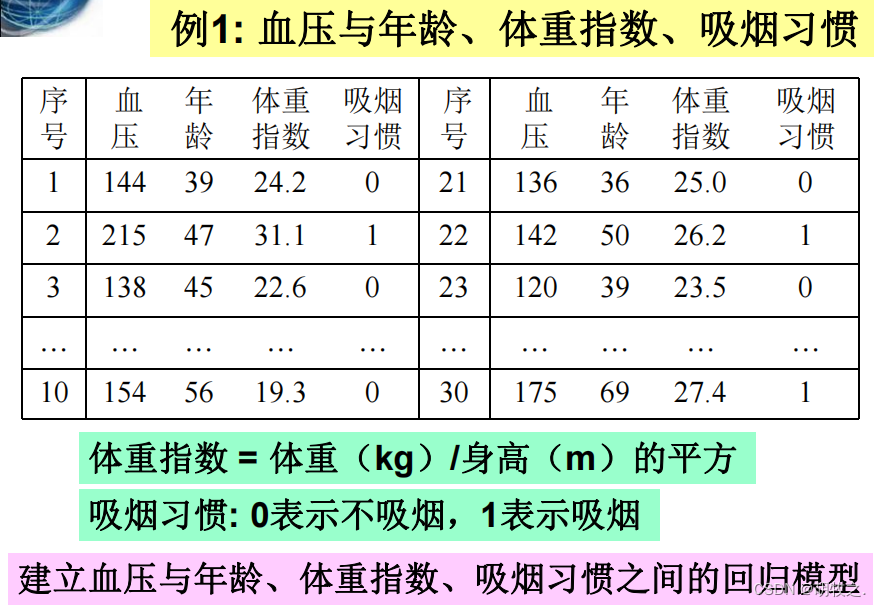
(二)模型建立
根据散点图情况,决定使用多元线性回归模型
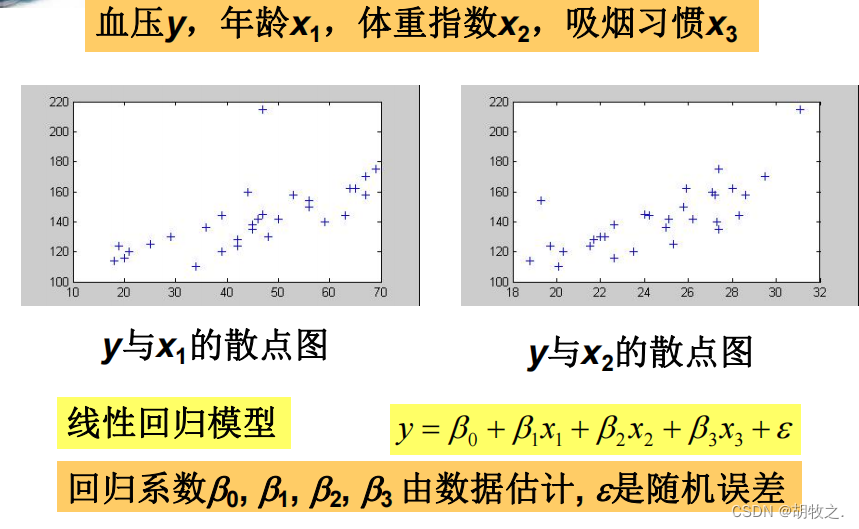
(三)模型求解( M A T L A B MATLAB MATLAB计算)

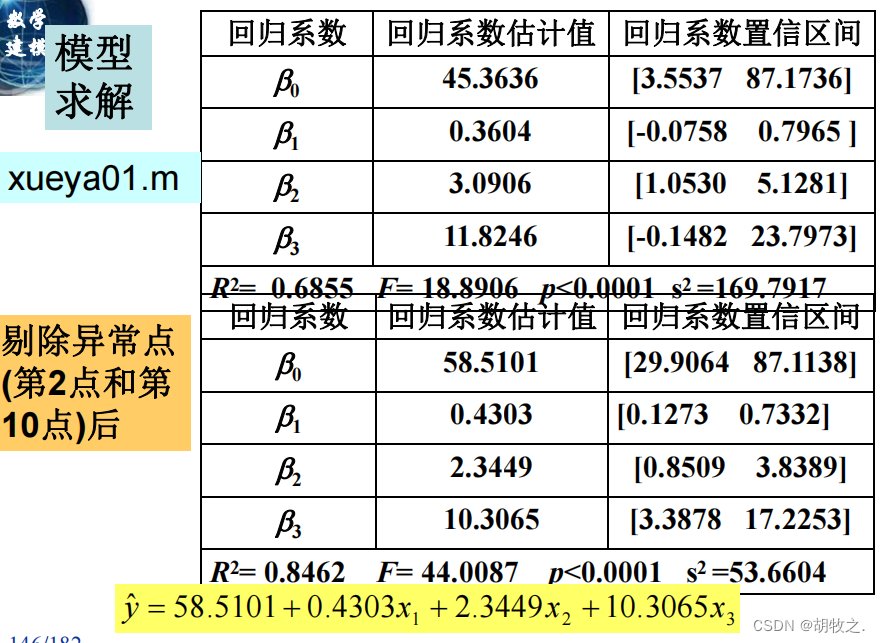
5.软件开发人员的薪金(薪金与资历、管理责任、教育程度)
(一)问题背景
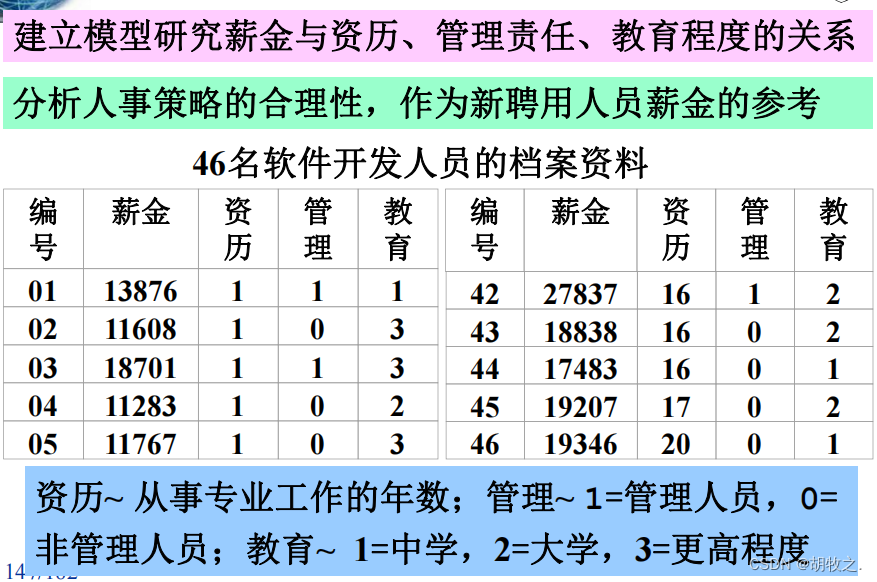
(二)模型建立(多元线性回归模型)

(三)模型求解
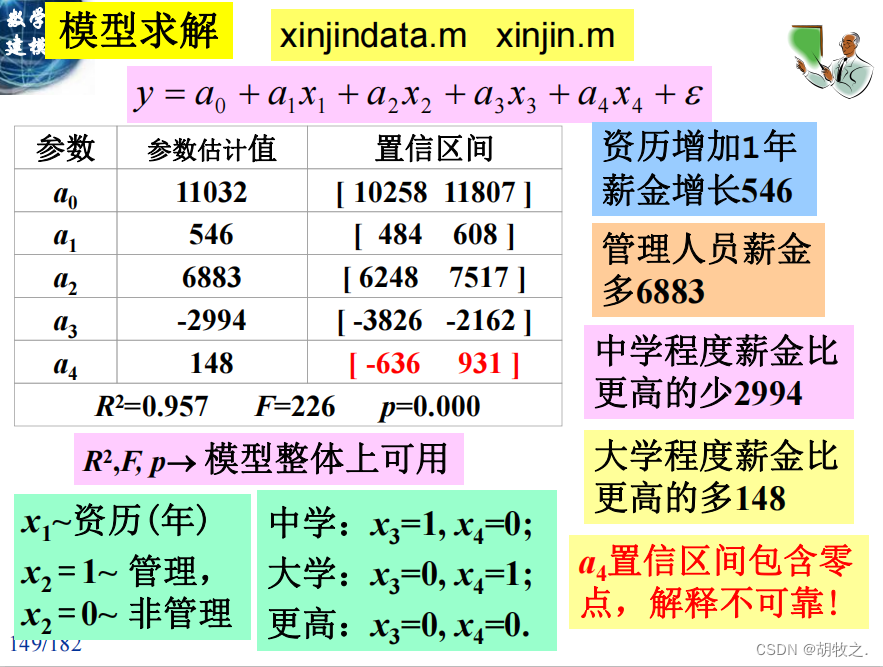
(四)结果分析(残差分析方法)

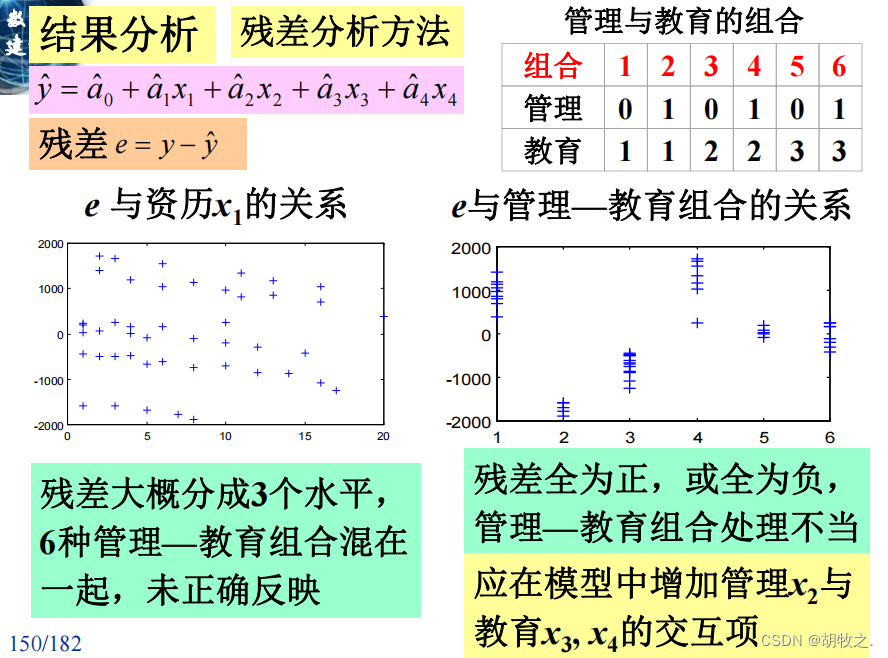
(五)增加管理与教育的交互项
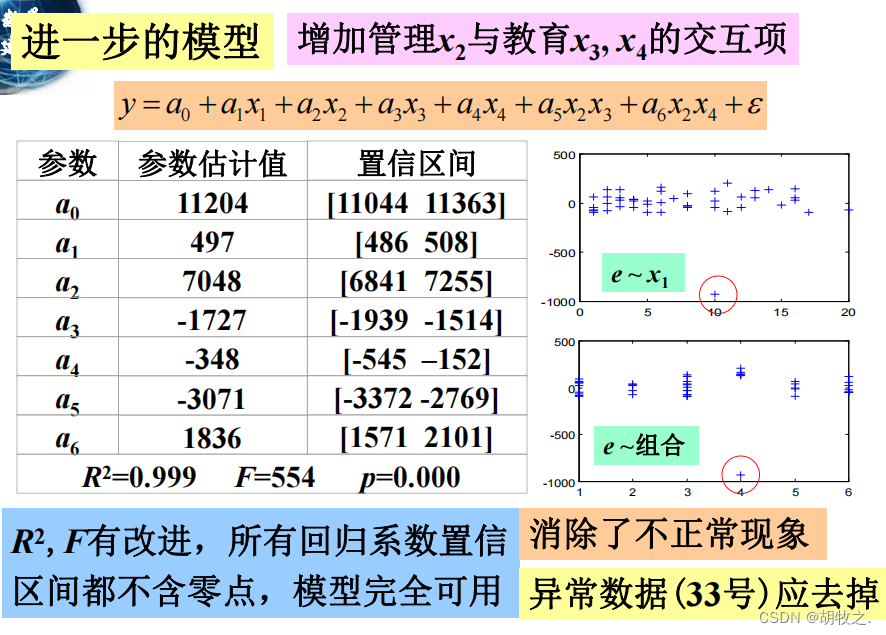
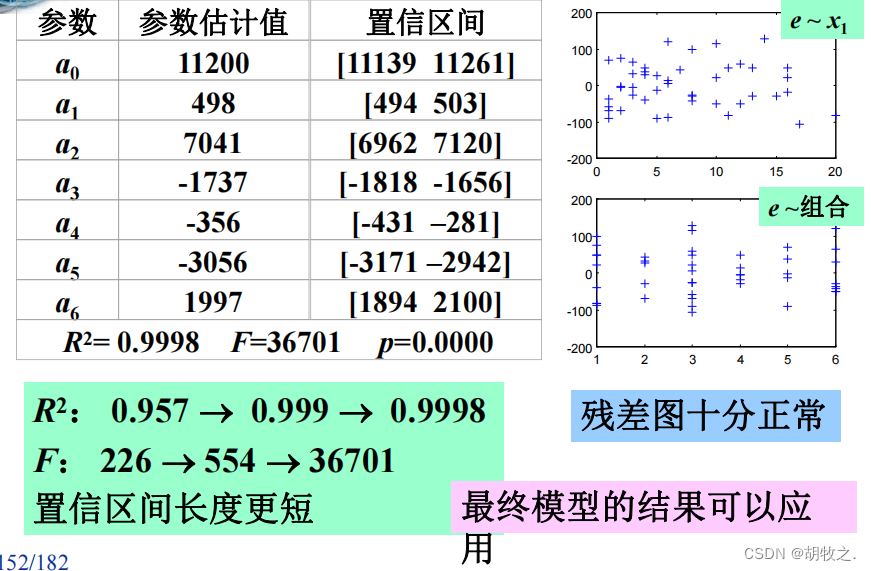
(六)模型应用
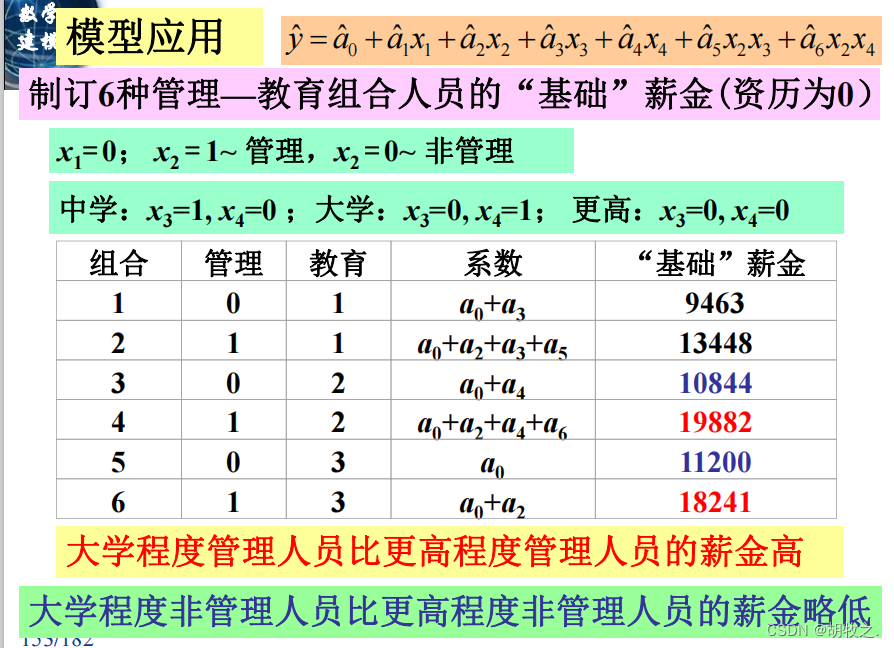

6.投资额与国民生产总值和物价指数(预测)
(一)问题背景
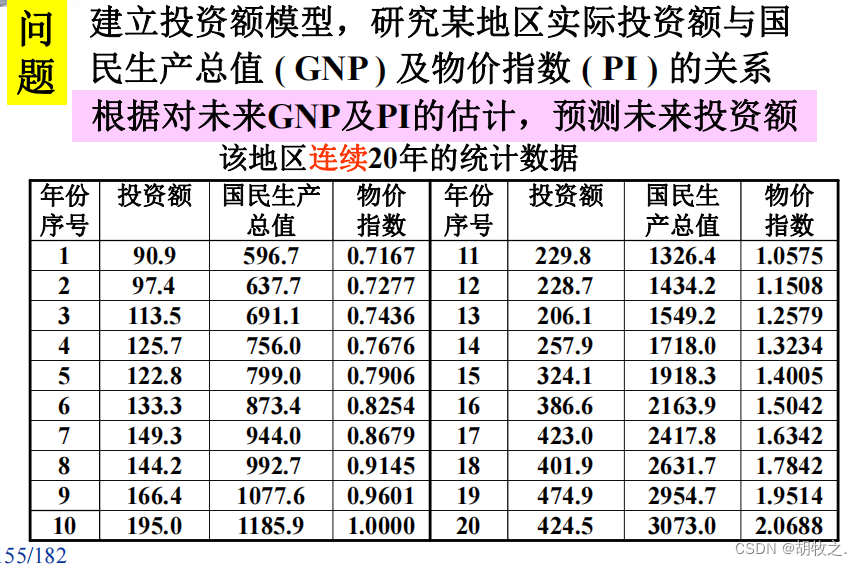
(二)问题分析
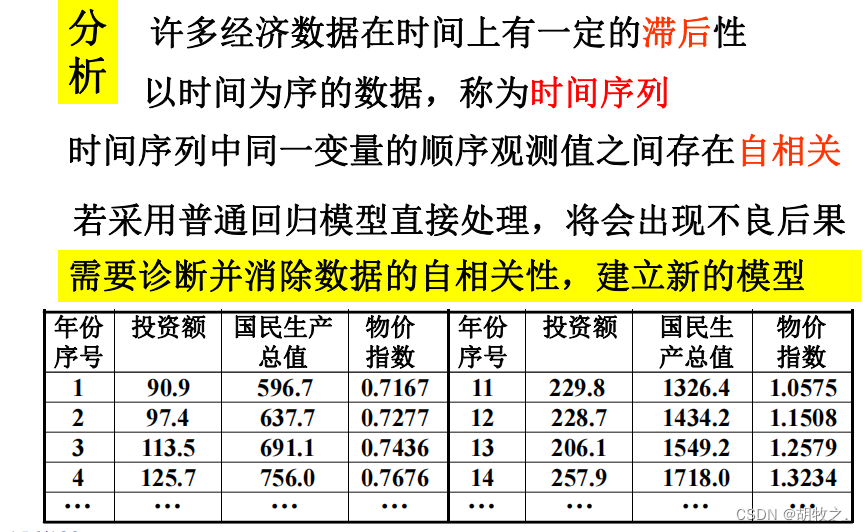
(三)基本模型建立(多元线性)
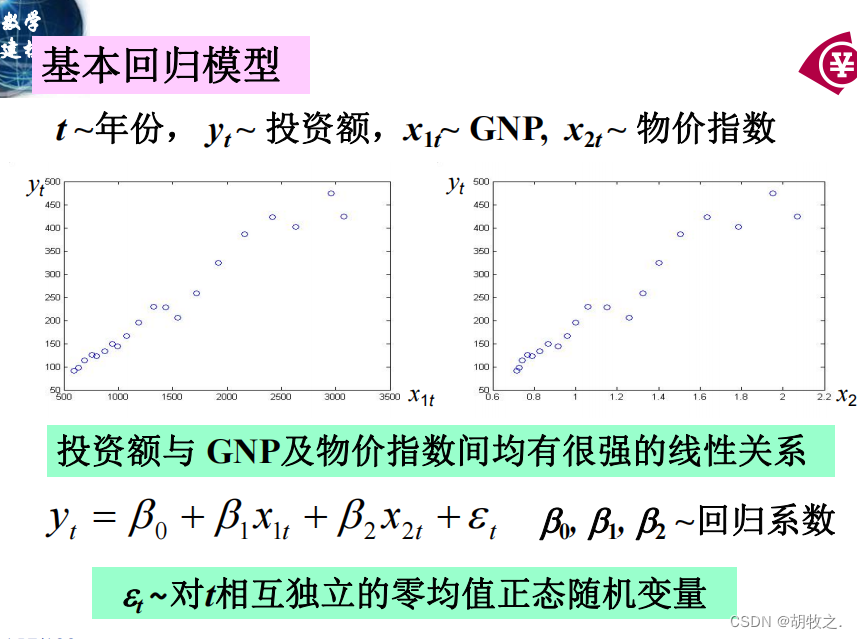
(四)基本回归模型结果分析( M A T L A B MATLAB MATLAB求解)
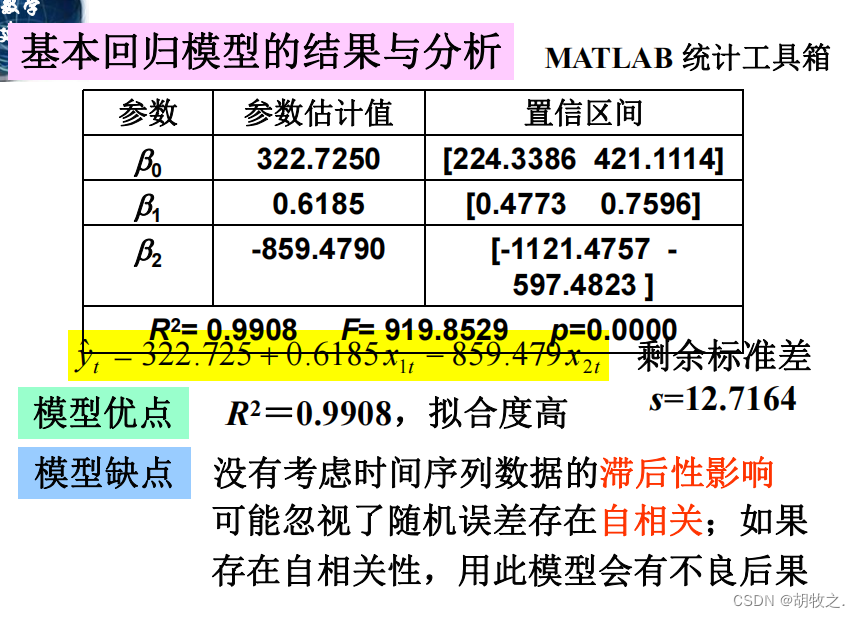
(五)自相关性——定性诊断(残差诊断法)
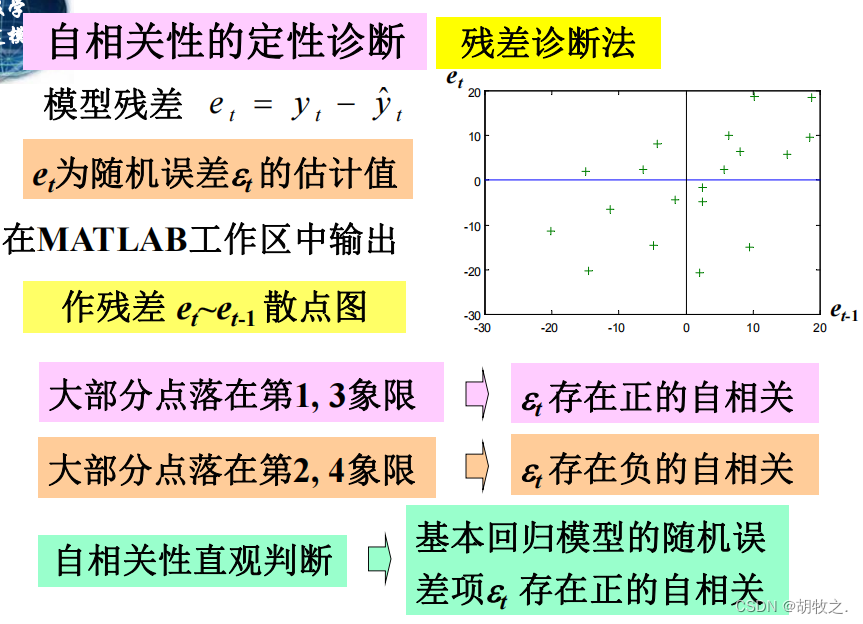
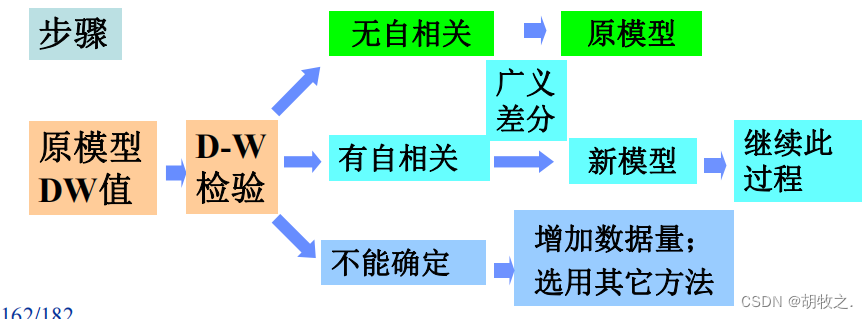
(六)自相关性——定量诊断(D-W检验)
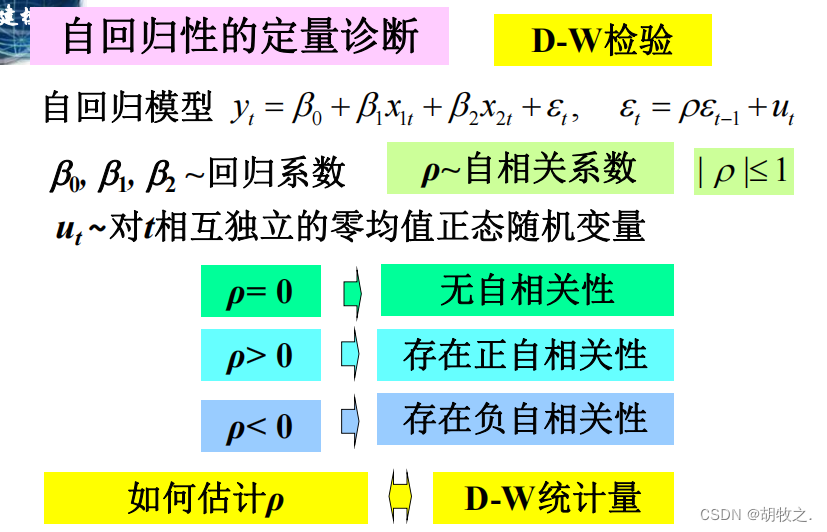
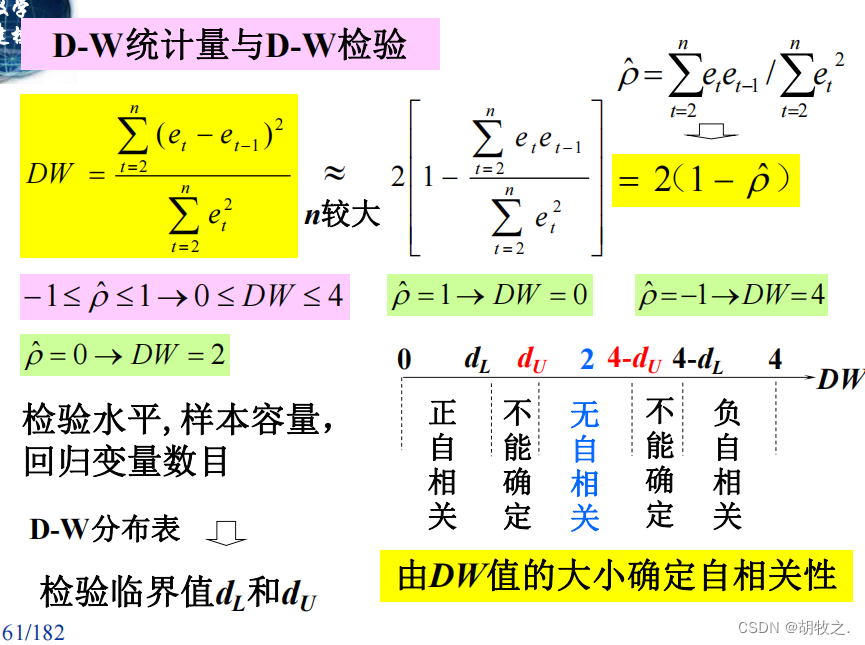
(七)自相关性——消除(广义差分法)

(八)新模型的建立
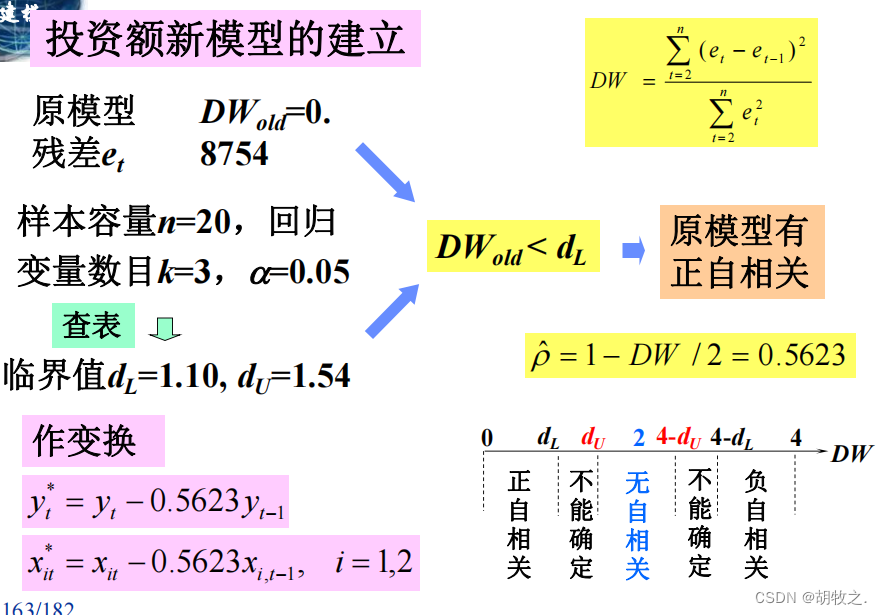
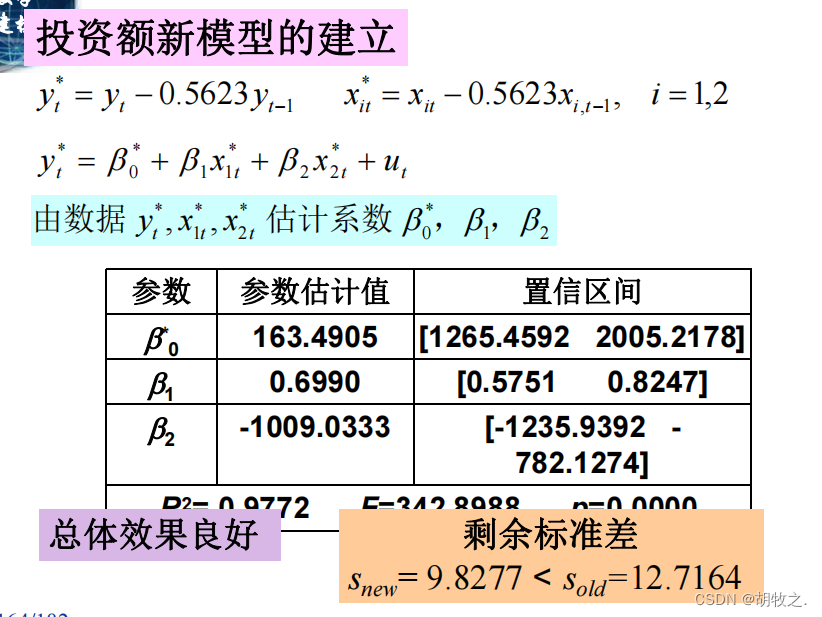

(九)两种模型的比较
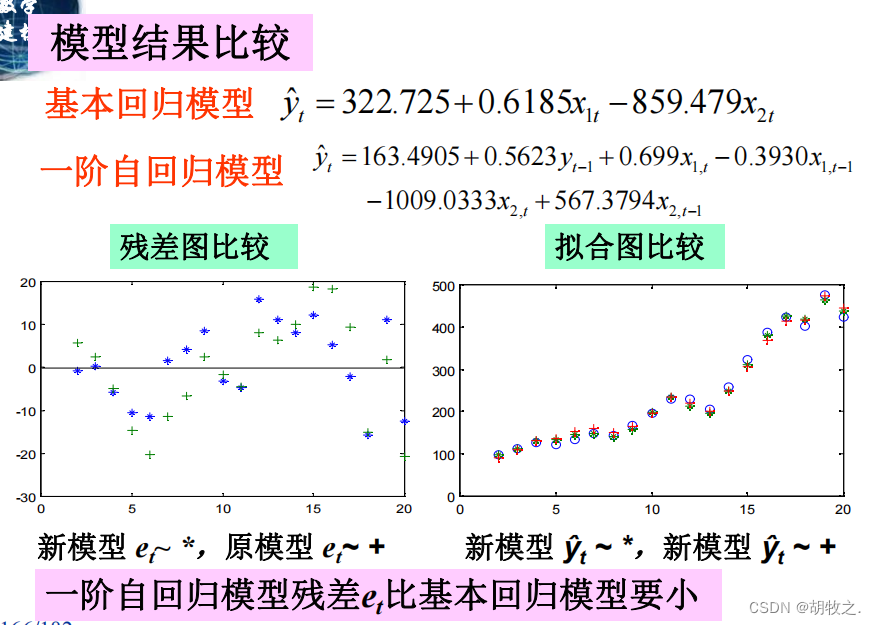
(十)投资额预测