前言：

一些博客就是转了Matlab 的中文说明，可是他那个说明，他自己都说了不是很对。

本文从实践出发，详细介绍Matlab对 坐标空间的点和向量的绘制方法。

---

1 点的概念和画法：

1.1 一个平面上的点

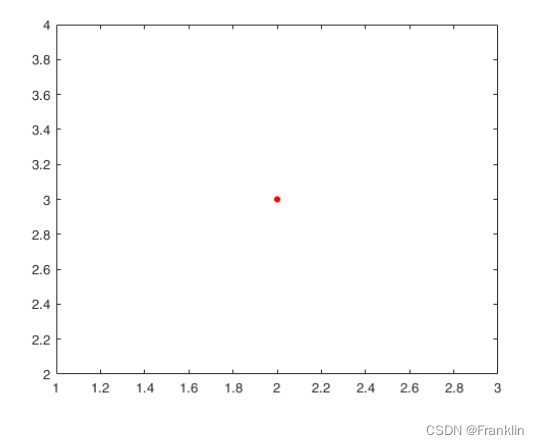
plot(2, 3, '.', 'MarkerSize', 16,"Color",'r');

【案】，这个例子里面，绘制了一个红色的点，坐标在笛卡尔坐标的(2,3)。

1.2 一个空间里的点：

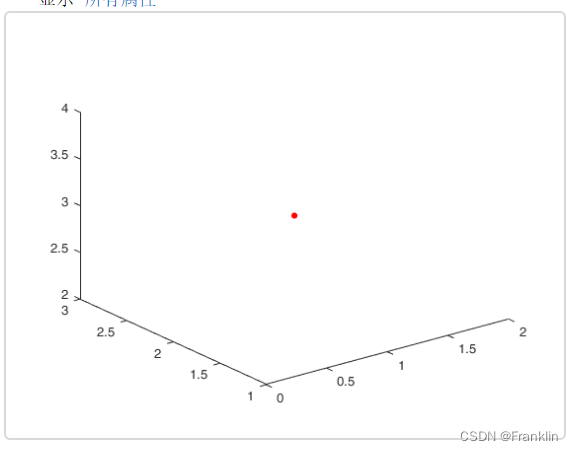
fig1 = figure(1)
plot3(1, 2,3, '.', 'MarkerSize', 16,"Color",'r')

1.3 一个空间里面2个点：

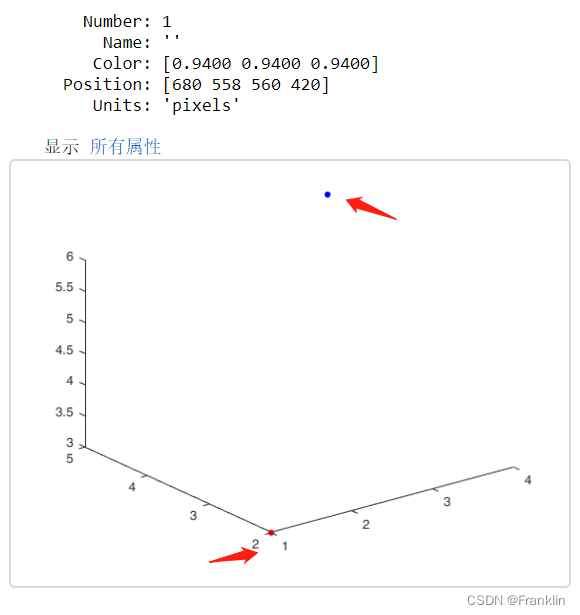
fig1 = figure(1)
plot3(1, 2,3, '.', 'MarkerSize', 16,"Color",'r')
hold on
plot3(4, 5,6, '.', 'MarkerSize', 16,"Color",'b')

---

向量的概念：

---

2 绘制向量的方法：

2.1 一个二维向量的绘制：

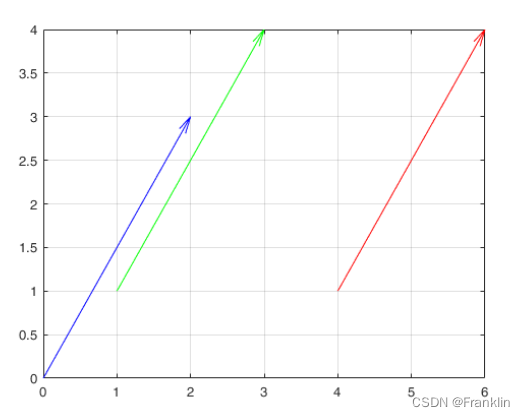
代码绘制了三个不同起点的向量， 

fig1 = figure(1)
scale = 1;
quiver(0,0,2,3,scale,'b');
grid on;
hold on;
quiver(1,1,2,3,scale,'g');
grid on;
hold on;
quiver(4,1,2,3,scale,'r');
grid on;
% 前面的两个数表示二维向量的起点坐标
% 后面的两个数表示二维向量的终点坐标
% scale=1表示对该向量的长度不进行任何伸缩
% 'b'代表蓝色

2.2 一个三维向量的绘制：

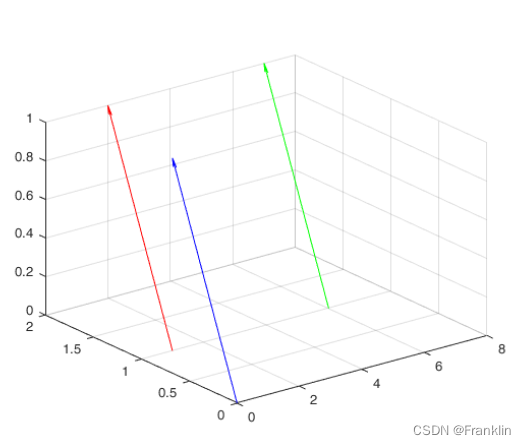
scale = 1;
quiver3(0,0,0,1,1,1,scale,'b');
hold on;
quiver3(1,1,0,1,1,1,scale,'r');
hold on;
quiver3(6,1,0,1,1,1,scale,'g');
% 前面的三个数表示三维向量的起点坐标
% 后面的三个数表示三维向量的终点坐标

---

2.3 向量加减的绘制：

 2.3.1 维度上

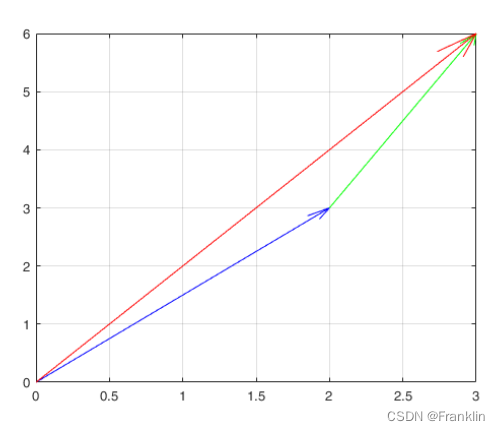
fig1 = figure(1)
scale = 1;
quiver(0,0,2,3,scale,'b');
grid on;
hold on;
quiver(2,3,1,3,scale,'g');
grid on;
hold on;
quiver(0,0,2+1,3+3,scale,'r');
grid on;

2.3.2 

 

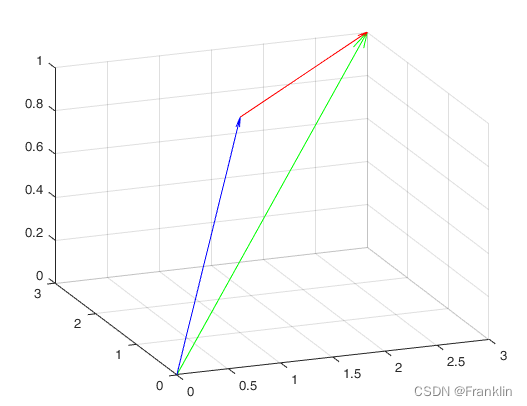
scale = 1;
quiver3(0,0,0,1,1,1,scale,'b');
hold on;
quiver3(1,1,1,2,2,0,scale,'r');
hold on;
quiver3(0,0,0,3,3,1,scale,'g');

---

3 使用参考：

1 函数：quiver 和向量场的画法

quiver(X,Y,U,V) plots arrows with directional components U and V at the Cartesian coordinates specified by X and Y.【X,Y为向量在笛卡尔的起点，向量的水平移动单位倍数为U，垂直移动单位倍数为V】【案，向量的理解中重要的概念就是instruction,就是指的向量的各个坐标分量的单位坐标步长数目】

For example, the first arrow originates from the point X(1) and Y(1), extends horizontally according to U(1), and extends vertically according to V(1). By default, the quiver function scales the arrow lengths so that they do not overlap.

【quiver 函数看起来就是遵循这个规则，后面的解释也是验证了这一段，从(1,1)为起点，然后垂直方向延伸【移动】一个单元v(1),然后水平方向延伸一个单元U(1),当然为了，避免向量箭头会重叠，他i自动缩放重叠的向量，这一段暂时还没有找到合适的例子来验证实践】

【官网，给出了一个绘制矢量图的例子，绘制北美风速的矢量图】

load wind.mat;
load('wind','x','y','u','v')
X = x(11:22,11:22,1);
Y = y(11:22,11:22,1);
U = u(11:22,11:22,1);
V = v(11:22,11:22,1);
quiver(X,Y,U,V)
axis equal

这里用到了wind.mat的开源数据：【这个在本文的下一节有介绍】

【Franklin案，这里选取了第11到22行，11到22列的位置的传感器1的位置和风速数据，然后调用quiver进行绘制，我们可以理解为，有12*12个向量组成的一个向量阵】

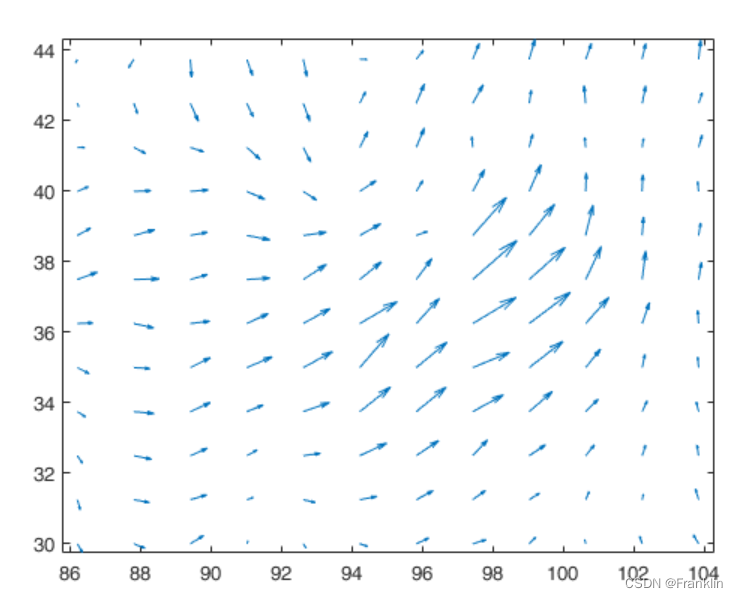
 【这里箭头的长度，就是向量的长度，比较形象展示了风的速度，同时quiver函数有避免重叠的功能，所以，部分向量的长度应该做了调整】

2 wind data

3-D data on air currents over North America. The data consists of (x,y,z) position components and (u,v,w) velocity components.

File Size: 142 KB

Data Size: Six matrices of size 35-by-41-by-15

load wind.mat
【wind data是一个3维的数据集，是北美空气流动的数据集，包括，xyz的一个位置元素，和一个uvw的速度元素，具体wind数据的使用，在MT的一个风能的视频介绍里面有很详细的解释】

用MT load 数据后，我们看的wind data的具体情况：

确实是6个矩阵，每个矩阵都是35-by-41-by-15

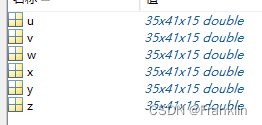
 我们先看一下位置数据x矩阵,Y矩阵，U矩阵：

可以看到表征位置的，XYZ的矩阵数据，在不同的行上X的值相同，Y值不同，但是，在Page 上对应的话，都是相同，有理由相信Page就是传感器的ID，大约有15个传感器。

然后，U,V的值为传感器测的不同反向上的风速等参数，这个数据随机性比较大。

X			Y			U
val(:,:,1) =	val(:,:,5) =		val(:,:,1) =	val(:,:,10) =		val(:,:,1) =	val(:,:,2) =
列 1	列 1
			列 1	列 1		列 1	列 1
70.1879	70.1879
70.1879	70.1879		17.4999	17.4999		0.5685	-2.8479
70.1879	70.1879		18.7499	18.7499		0.5685	-2.8479
70.1879	70.1879		19.9999	19.9999		0.5685	-2.8479
70.1879	70.1879		21.2499	21.2499		0.8791	-2.2267
70.1879	70.1879		22.4999	22.4999		1.1897	-1.295
70.1879	70.1879		23.7499	23.7499		1.5003	-0.3632
70.1879	70.1879		24.9999	24.9999		1.5003	0.5685
70.1879	70.1879		26.2499	26.2499		2.1214	2.1214
70.1879	70.1879		27.4999	27.4999		3.0531	3.3637
70.1879	70.1879		28.7499	28.7499		4.606	6.1589
70.1879	70.1879		29.9999	29.9999		4.606	7.4013
70.1879	70.1879		31.2499	31.2499		4.9166	9.2647
70.1879	70.1879		32.4999	32.4999		4.9166	10.507
70.1879	70.1879		33.7499	33.7499		5.2272	13.9234
70.1879	70.1879		34.9999	34.9999		5.2272	15.4763
70.1879	70.1879		36.2499	36.2499		5.2272	15.4763
70.1879	70.1879		37.4999	37.4999		5.5378	17.0292
70.1879	70.1879		38.7499	38.7499		6.1589	20.135
70.1879	70.1879		39.9999	39.9999		5.5378	19.8244
70.1879	70.1879		41.2499	41.2499		3.3637	18.2715
70.1879	70.1879		42.4999	42.4999		1.5003	13.9234
70.1879	70.1879		43.7499	43.7499		0.8791	10.507
70.1879	70.1879		44.9999	44.9999		0.2579	5.2272
70.1879	70.1879		46.2499	46.2499		-0.6738	1.5003
70.1879	70.1879		47.4999	47.4999		-2.2267	-3.1584
70.1879	70.1879		48.7499	48.7499		-3.1584	-5.6431
70.1879	70.1879		49.9999	49.9999		-3.7796	-5.6431
70.1879	70.1879		51.2499	51.2499		-4.4008	-6.8854
70.1879	70.1879		52.4999	52.4999		-4.7113	-8.4383
70.1879	70.1879		53.7499	53.7499		-3.7796	-8.1277
70.1879	70.1879		54.9999	54.9999		-2.5373	-7.196
70.1879	70.1879		56.2499	56.2499		-1.295	-6.2642
70.1879	70.1879		57.4999	57.4999		-0.9844	-4.7113
70.1879	70.1879		58.7499	58.7499		-1.295	-3.1584
			59.9999	59.9999		-2.5373	-2.8479

列 2	列 2
			列 2	列 2		列 2	列 2
71.7907	71.7907
71.7907	71.7907		17.4999	17.4999		0.5685	-2.5373
71.7907	71.7907		18.7499	18.7499		0.5685	-2.5373
71.7907	71.7907		19.9999	19.9999		0.8791	-2.5373
71.7907	71.7907		21.2499	21.2499		0.8791	-1.6055
71.7907	71.7907		22.4999	22.4999		1.1897	-0.9844
71.7907	71.7907		23.7499	23.7499		1.5003	0.2579
71.7907	71.7907		24.9999	24.9999		1.1897	0.5685
71.7907	71.7907		26.2499	26.2499		2.1214	3.0531
71.7907	71.7907		27.4999	27.4999		3.6743	5.5378
71.7907	71.7907		28.7499	28.7499		3.3637	6.1589
71.7907	71.7907		29.9999	29.9999		3.3637	7.0907
71.7907	71.7907		31.2499	31.2499		4.2955	8.6436
71.7907	71.7907		32.4999	32.4999		4.9166	9.5753
71.7907	71.7907		33.7499	33.7499		5.2272	12.0599
71.7907	71.7907		34.9999	34.9999		5.5378	16.408
71.7907	71.7907		36.2499	36.2499		4.9166	17.3398
71.7907	71.7907		37.4999	37.4999		4.9166	16.408
71.7907	71.7907		38.7499	38.7499		4.606	16.7186
71.7907	71.7907		39.9999	39.9999		4.606	17.0292
71.7907	71.7907		41.2499	41.2499		4.2955	17.0292
71.7907	71.7907		42.4999	42.4999		0.5685	12.0599
71.7907	71.7907		43.7499	43.7499		1.5003	9.5753
71.7907	71.7907		44.9999	44.9999		0.8791	5.5378
71.7907	71.7907		46.2499	46.2499		0.2579	2.432
71.7907	71.7907		47.4999	47.4999		-1.6055	-2.8479
71.7907	71.7907		48.7499	48.7499		-2.5373	-5.3325
71.7907	71.7907		49.9999	49.9999		-2.8479	-5.6431
71.7907	71.7907		51.2499	51.2499		-2.8479	-6.2642
71.7907	71.7907		52.4999	52.4999		-3.469	-6.8854
71.7907	71.7907		53.7499	53.7499		-2.8479	-6.8854
71.7907	71.7907		54.9999	54.9999		-1.295	-6.2642
71.7907	71.7907		56.2499	56.2499		-0.6738	-4.4008
71.7907	71.7907		57.4999	57.4999		-2.2267	-3.1584
71.7907	71.7907		58.7499	58.7499		-2.8479	-3.7796
			59.9999	59.9999		-2.8479	-2.8479

---

参考：

Quiver or vector plot - MATLAB quiver (mathworks.com)

 matlab中向量的绘制方法_陈腾飞同学的博客-CSDN博客_matlab画向量

Matlab 画向量图和平面图 - 知乎 (zhihu.com)