什么是转移概率矩阵(Transition Probability Matrix)
转移概率矩阵:矩阵各元素都是非负的,并且各行元素之和等于1,各元素用概率表示,在一定条件下是互相转移的,故称为转移概率矩阵。如用于市场决策时,矩阵中的元素是市场或顾客的保留、获得或失去的概率。P(k)表示k步转移概率矩阵。
转移概率矩阵的特征
转移概率矩阵有以下特征:
①,0≤Pij≤1
②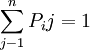 ,即矩阵中每一行转移概率之和等于1。
,即矩阵中每一行转移概率之和等于1。
转移概率矩阵的分析
所谓矩阵,是指许多个数组成的一个数表。每个数称为矩阵的元素。矩阵的表示方法是用括号将矩阵中的元素括起来,以表示它是一个整体。如A就是一个矩阵。
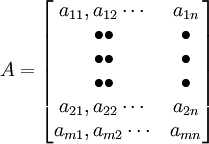
这是一个由m行n列的数构成的矩阵, 表示位于矩阵中第i行与第j列交叉点上的元素, 矩阵中的行数与列数可以相等,也可以不等。当它们相等时,矩阵就是一个方阵。
由转移概率组成的矩阵就是转移概率矩阵。也就是说构成转移概率矩阵的元素是一个个的转移概率。
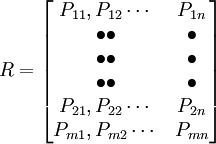
转移概率与转移概率矩阵[1]
假定某大学有1万学生,每人每月用1支牙膏,并且只使用“中华”牙膏与“黑妹”牙膏两者之一。根据本月(12月)调查,有3000人使用黑妹牙膏,7000人使用中华牙膏。又据调查,使用黑妹牙膏的3000人中,有60%的人下月将继续使用黑妹牙膏,40%的人将改用中华牙膏; 使用中华牙膏的7000人中, 有70%的人下月将继续使用中华牙膏,30%的人将改用黑妹牙膏。据此,可以得到如表-1所示的统计表。
表-1 两种牙膏之间的转移概率
| 拟用 | 黑妹牙膏 | 中华牙膏 |
|---|---|---|
| 现用 | ||
| 黑妹牙膏 | 60% | 40% |
| 中华牙膏 | 30% | 70% |
上表中的4个概率就称为状态的转移概率,而这四个转移概率组成的矩阵
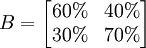
称为转移概率矩阵。可以看出, 转移概率矩阵的一个特点是其各行元素之和为1。 在本例中,其经济意义是:现在使用某种牙膏的人中,将来使用各种品牌牙膏的人数百分比之和为1。
2. 用转移概率矩阵预测市场占有率的变化
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
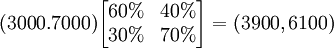
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。
假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
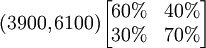
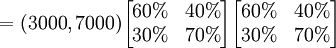
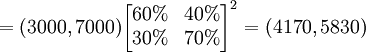
这里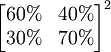 称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
转移概率矩阵案例分析
案例一: 用转移概率矩阵预测市场占有率的变化[1]
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
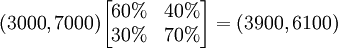
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
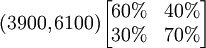
=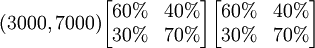
=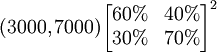
=(4170,5830)
这里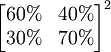
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
参考文献
- ↑ 1.0 1.1 决策支持系统导论.第二章 市场需求预测与预测支持系统
相关条目
- 转移概率
- 马尔可夫过程
转移概率(transition probability)
什么是转移概率
转移概率是马尔可夫链中的重要概念,若马氏链分为m个状态组成,历史资料转化为由这m个状态所组成的序列。从任意一个状态出发,经过任意一次转移,必然出现状态1、2、……,m中的一个,这种状态之间的转移称为转移概率。
当样本中状态m可能发生转移的总次数为i,而由状态m到未来任一时刻转为状态ai的次数时,则在m+n时刻转移到未来任一时刻状态aj的转移概率为:
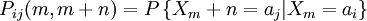
这些转移移概率可以排成一个的转移概率矩阵:P(m,m+n)(Pij(m,m + n))
当m=1时为一阶转概率矩阵,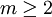 时为高阶概率转移矩阵,有了概率转移矩阵,就得到了状态之间经一步和多步转移的规律,这些规律就是贷款状态间演变规律的表,当初始状态已知时,可以查表做出不同时期的预测。
时为高阶概率转移矩阵,有了概率转移矩阵,就得到了状态之间经一步和多步转移的规律,这些规律就是贷款状态间演变规律的表,当初始状态已知时,可以查表做出不同时期的预测。
转移概率与转移概率矩阵[1]
假定某大学有1万学生,每人每月用1支牙膏,并且只使用“中华”牙膏与“黑妹”牙膏两者之一。 根据本月(12月)调查,有3000人使用黑妹牙膏,7000人使用中华牙膏。 又据调查,使用黑妹牙膏的3000人中, 有60%的人下月将继续使用黑妹牙膏, 40%的人将改用中华牙膏; 使用中华牙膏的7000人中, 有70%的人下月将继续使用中华牙膏, 30%的人将改用黑妹牙膏。据此,可以得到如表-1所示的统计表。
表-1 两种牙膏之间的转移概率
| 拟用 | 黑妹牙膏 | 中华牙膏 |
|---|---|---|
| 现用 | ||
| 黑妹牙膏 | 60% | 40% |
| 中华牙膏 | 30% | 70% |
上表中的4个概率就称为状态的转移概率,而这四个转移概率组成的矩阵
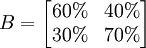
称为转移概率矩阵。可以看出, 转移概率矩阵的一个特点是其各行元素之和为1。 在本例中,其经济意义是:现在使用某种牙膏的人中,将来使用各种品牌牙膏的人数百分比之和为1。
2. 用转移概率矩阵预测市场占有率的变化
有了转移概率矩阵,就可以预测,到下个月(1月份)使用黑妹牙膏和中华牙膏的人数,计算过程如下:
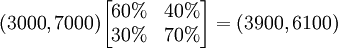
即:1月份使用黑妹牙膏的人数将为3900,而使用中华牙膏的人数将为6100。
假定转移概率矩阵不变,还可以继续预测到2月份的情况为:
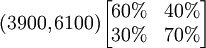
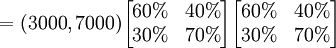
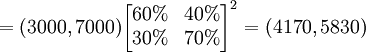
这里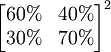 称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
称为二步转移矩阵,也即由12月份的情况通过2步转移到2月份的情况。二步转移概率矩阵正好是一步转移概率矩阵的平方。一般地, k步转移概率矩阵
正好是一步转移概率矩阵的k次方。可以证明,k步转移概率矩阵中,各行元素之和也都为1。
马尔可夫过程(Markov Process)
什么是马尔可夫过程
1、马尔可夫性(无后效性)
过程或(系统)在时刻t0所处的状态为已知的条件下,过程在时刻t > t0所处状态的条件分布,与过程在时刻t0之前年处的状态无关的特性称为马尔可夫性或无后效性。
即:过程“将来”的情况与“过去”的情况是无关的。
2、马尔可夫过程的定义
具有马尔可夫性的随机过程称为马尔可夫过程。
用分布函数表述马尔可夫过程:
设I:随机过程{X(t),t\in T}的状态空间,如果对时间t的任意n个数值:
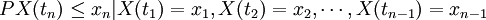 (注:X(tn)在条件X(ti) = xi下的条件分布函数)
(注:X(tn)在条件X(ti) = xi下的条件分布函数)
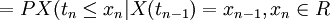 (注:X(tn))在条件X(tn − 1) = xn − 1下的条件分布函数)
(注:X(tn))在条件X(tn − 1) = xn − 1下的条件分布函数)
或写成:
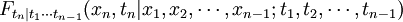
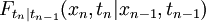
这时称过程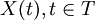 具马尔可夫性或无后性,并称此过程为马尔可夫过程。
具马尔可夫性或无后性,并称此过程为马尔可夫过程。
3、马尔可夫链的定义
时间和状态都是离散的马尔可夫过程称为马尔可夫链, 简记为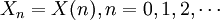 。
。
马尔可夫过程的概率分布
研究时间和状态都是离散的随机序列: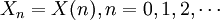 ,状态空间为
,状态空间为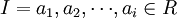
1、用分布律描述马尔可夫性
对任意的正整数n,r和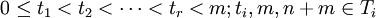 ,有:
,有:
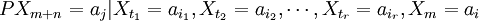
PXm + n = aj | Xm = ai,其中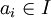 。
。
2、转移概率
称条件概率Pij(m,m + n) = PXm + n = aj | Xm = ai为马氏链在时刻m处于状态ai条件下,在时刻m+n转移到状态aj的转移概率。
说明:转移概率具胡特点:
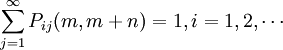 。
。
由转移概率组成的矩阵![]() 称为马氏链的转移概率矩阵。它是随机矩阵。
称为马氏链的转移概率矩阵。它是随机矩阵。
3、平稳性
当转移概率Pij(m,m + n)只与i,j及时间间距n有关时,称转移概率具有平稳性。同时也称些链是齐次的或时齐的。
此时,记Pij(m,m + n) = Pij(n),Pij(n) = PXm + n = aj | Xm = ai(注:称为马氏链的n步转移概率)
P(n) = (Pij(n))为n步转移概率矩阵。
特别的, 当 k=1 时,
一步转移概率:Pij = Pij(1) = PXm + 1 = aj | Xm = ai。
一步转移概率矩阵:P(1)

马尔可夫过程的应用举例
设任意相继的两天中,雨天转晴天的概率为1/3,晴天转雨天的概率为1/2,任一天晴或雨是互为逆事件。以0表示晴天状态,以1表示雨天状态,Xn表示第n天状态(0或1)。试定出马氏链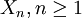 的一步转移概率矩阵。又已知5月1日为晴天,问5月3日为晴天,5月5日为雨天的概率各等于多少?
的一步转移概率矩阵。又已知5月1日为晴天,问5月3日为晴天,5月5日为雨天的概率各等于多少?
解:由于任一天晴或雨是互为逆事件且雨天转晴天的概率为1/3,晴天转雨天的概率为1/2,故一步转移概率和一步转移概率矩阵分别为:
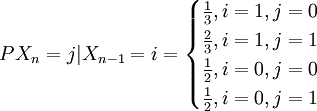
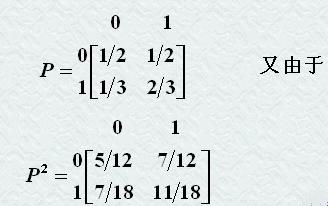
故5月1日为晴天,5月3日为晴天的概率为:
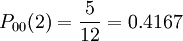
又由于:
故5月1日为晴天,5月5日为雨天的概率为:P01(4) = 0.5995
这人写的太好了,情不自禁的转载http://blog.sina.com.cn/s/blog_68c4a1b501015es8.html