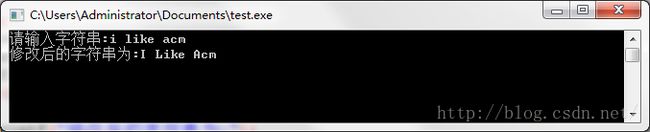
代码

方法1：袖珍计算器算法，使用其他数学公式
$\sqrt{x}=x^{\frac{1}{2}}=(e^{lnx})^{\frac{1}{2}}=e^{\frac{1}{2}lnx}$

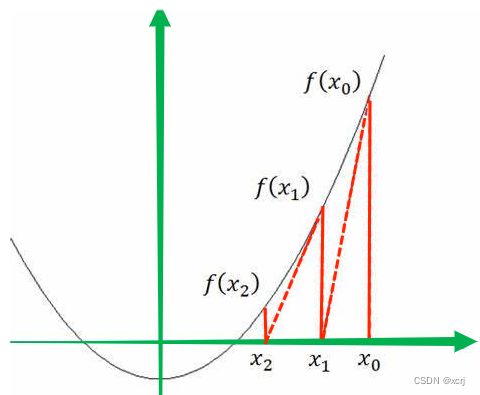
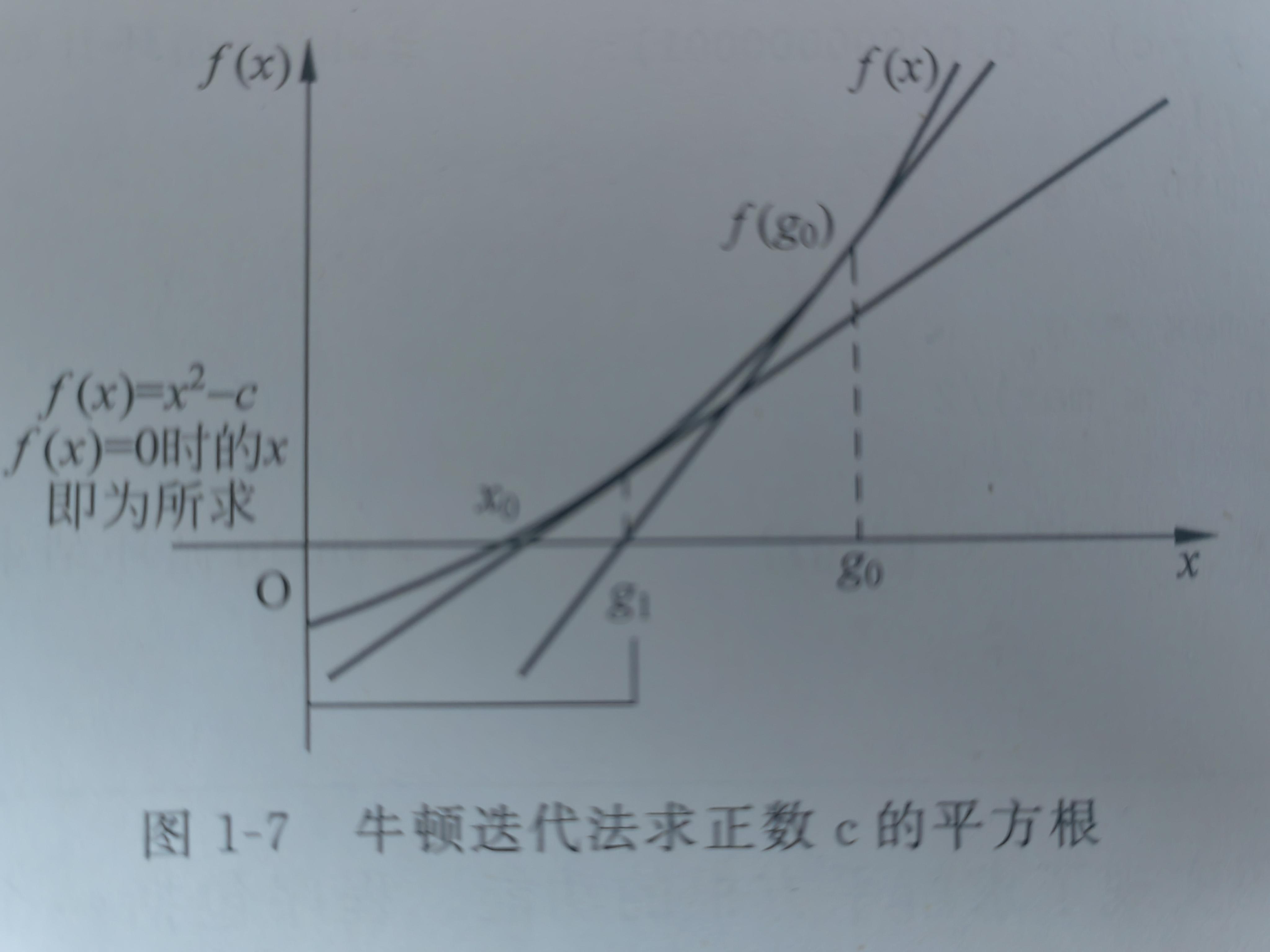
方法3：牛顿迭代法泰勒级数展开逼近真解，y=x^2-C，C代表待求x，逼近真解
在这里插入图片描述

package com.xcrj;/*** 剑指 Offer II 072. 求平方根* - 给定一个非负整数 x ，计算并返回 x 的平方根，即实现int sqrt(int x)函数。* - 正数的平方根有两个，只输出其中的正数平方根。* - 如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。*/
public class Solution72 {/*** 袖珍计算器算法* 使用其他数学公式（使用语言内置的函数，计算速度快）*/public int mySqrt1(int x) {if (0 == x) return 0;/***  Math.log(x)的base是e*  (int)：获取结果的整数部分*  浮点数的计算结果存在误差，取整之后，错误结果+1=正确结果*  例如，x=2147395600，r错误=46339，r正确结果=46340*/int r = (int) Math.exp(0.5 * Math.log(x));/*** 若r是正确答案则(r+1)*(r+1)>x* 若r是错误答案则r+1 todo* long：防止相乘越界*/return (long) (r + 1) * (r + 1) > x ? r : r + 1;}/*** 二分查找k^2仅小于x的k*/public int mySqrt2(int x) {if (0 == x) return 0;int l = 0, r = x, o = -1;// l=r，因为r=xwhile (l <= r) {int mid = ((r - l) >> 1) + l;// 找仅小于x的k，小于则往右侧靠拢逼近xif ((long) mid * mid <= x) {o = mid;l = mid + 1;}// 找仅小于x的k，大于则往左侧靠拢逼近xelse {// mid*mid<=x 已经跟x比较过了r = mid - 1;}}return o;}/*** 牛顿迭代法 浮点* - 本质是借助泰勒级数，从初始值开始快速向零点逼近，向真解逼近* <p>* 过程* - 构建函数，y=x^2-C，C代表待求x* - 初始点x0，x0=输入x。这种构建可以获取正数解* - 构建点x1，由y在x0处的斜率k0和y上的点(x0,y0)构成的直线与x轴的交点得到x1* -- 构建点x2，由y在x1处的斜率k1和y上的点(x1,y1)构成的直线与x轴的交点得到x2* -- 构建点xi，...* --- 根据直线与x轴交点求的xi=0.5 * (x_(i-1) + C / x_(i-1))* - 靠近程度：xi不停的靠近真解，直到x_(i-1)和xi的差值小于1e-7* -- 在xi不停靠近真解的过程中，x_(i-1)和xi之间的差值越来越小。因为y函数越来越平坦*/public int mySqrt3(int x) {if (0 == x) return 0;// C代表待求xdouble C = x;// 初始点x0，x0=输入x。这种构建可以获取正数解double x0 = x;// xpre=x_(i-1)代表前一个解double xpre = x0;while (true) {// 根据直线与x轴交点求的xidouble xi = 0.5 * (xpre + C / xpre);// 在xi不停靠近真解的过程中，x_(i-1)和xi之间的差值越来越小。因为y函数越来越平坦if (Math.abs(xi - xpre) < 1e-7) {return (int) xi;}xpre = xi;}}/*** 牛顿迭代法 整数*/public int mySqrt4(int x) {if (0 == x) return 0;// C代表待求xint C = x;// 初始点x0，x0=输入x。这种构建可以获取正数解int x0 = x;// xpre=x_(i-1)代表前一个解long xpre = x0;while (true) {// 根据直线与x轴交点求的xilong xi = (xpre + C / xpre) / 2;// 在xi不停靠近真解的过程中，xi * xi逐渐靠近xif (xi * xi <= x) {return (int) xi;}xpre = xi;}}
}