数据挖掘经典十大算法

一、ID3算法介绍

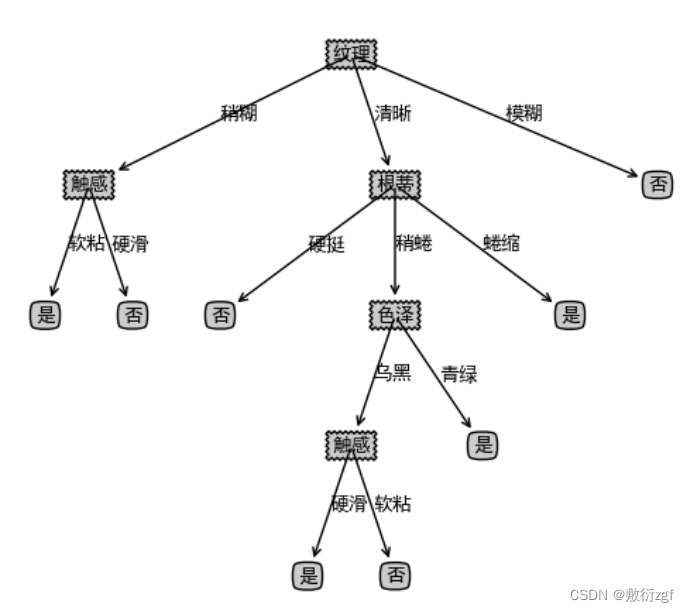
ID3算法通过自顶向下的方式构建一棵决策树来进行学习，每一次选择的是当前样本集中具有最大信息增益的属性作为测试属性。样本集根据测试属性的属性值进行划分，测试属性有多少取值就能够将样本属性划分为多少子样本集。
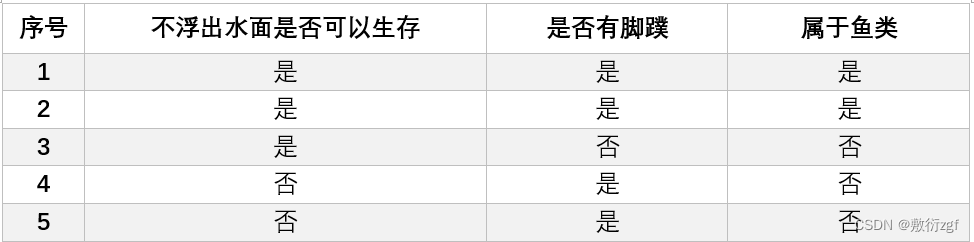
海洋生物数据
构建决策树：
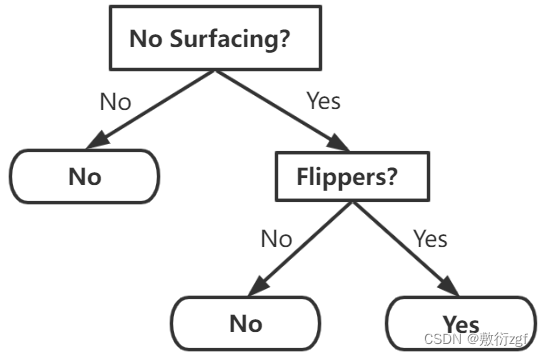
在这里插入图片描述

二、利用python实现ID3算法

ID3.py

import math
import operator
import TreePlotter
# 1.构建西瓜数据集 离散属性
def createDataset() :# 特征列表features = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']dataset = [# 数组中的每一个元素为一个样本共17个，属性有6个  最后一个是分类标签['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'],['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'],['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'],['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '是'],['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '是'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '是'],['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '否'],['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '否'],['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '否'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '否'],['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '否'],['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '否'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '否'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '否'],['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '否']]return dataset , features # 返回数据集和特征列表'''
5.函数说明:计算给定数据集的经验熵(香农熵)
Parameters:dataSet - 数据集
Returns:shannonEnt - 经验熵(香农熵)
'''
def calcShannonEnt(dataSet) :numEntries = len(dataSet) # 计算数据中的样本数(行数)labelCount = {} # 计算每个类的样本数(每个标签出现的次数) 采用字典存放for featVec in dataSet : # 对每一组特征向量进行统计if featVec[-1] not in labelCount.keys() : # featVec[-1]提取标签信息  如果标签中没有放入统计次数的字典中，将其添加labelCount[featVec[-1]] = 0labelCount[featVec[-1]] += 1 # 计数+1shannonEnt = 0 # 设置香农熵的初始值for key in labelCount : # 计算香农熵prob = float(labelCount[key]) / numEntries # 该标签的个数/总的样本数 表示选择该标签的概率 强制转换为float类型shannonEnt -= prob * math.log(prob,2) # 利用信息熵公式 E(x) = -p(x)*logp(x) 以2为底return shannonEnt # 返回香农熵'''
6.函数说明:按照给定特征划分数据集
Parameters:dataSet - 待划分的数据集axis - 划分数据集的特征value - 需要返回的特征的值
'''
def splitDataSet(dataSet,axis,value) : # axis属性索引 value属性取值retDataSet = [] # 列表用于保存筛选出来的数据样本for featVec in dataSet : # 遍历数据集if featVec[axis] == value :reducedFeatVec = featVec[:axis] # 去掉axis特征reducedFeatVec.extend(featVec[axis + 1 :]) # 将符合条件的添加到返回的数据集中retDataSet.append(reducedFeatVec)return retDataSet # 返回划分后的数据集'''
4.函数说明:选择最优特征
Parameters:dataSet - 数据集
Returns:bestFeature - 信息增益最大的(最优)特征的索引值
'''
def chooseBestFeatureToSplit(dataSet):numFeatures = len(dataSet[0]) - 1 # -1是为了去除最后一列 保存特征数量baseEntropy = calcShannonEnt(dataSet) # 调用自定义方法计算香农熵bestInfoGain = 0.0 # 设置初始信息增益bestFeature = -1 # 设置初始最有特征的属性索引是 -1for i in range(numFeatures) : # 遍历所有的特征# 获取dataSet的第i个所有特征featList = [example[i] for example in dataSet]uniqueVals = set(featList) # 创建set集合 元素不重复newEntropy = 0 # 设置经验条件熵的初始值for value in uniqueVals : # 计算信息增益subDataSet = splitDataSet(dataSet,i,value) # splitDataSet划分后的子集prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率 划分后的子集/总的样本数量newEntropy += prob * calcShannonEnt(subDataSet) # 利用香浓熵计算经验条件熵infoGain = baseEntropy - newEntropy # 计算信息增益 香农熵-条件熵if infoGain > bestInfoGain : # 将新计算的信息增益进行比较bestInfoGain = infoGain # 更新 使得bestInfoGain中一直保存的是最大的信息增益bestFeature = i # 记录信息增益最大的特征的索引值return bestFeature # 返回信息增益最大的(最优)特征的索引值'''
3.函数说明:统计classList中出现次数最多的元素(类标签)
Parameters:classList - 类标签列表
Returns:sortedClassCount[0][0] - 出现次数最多的元素(类标签)
'''
def majorityCnt(classList) :classCount = {} # 采用字典计数for value in classList : # 遍历类标签列表 统计classList中每个元素出现的次数if value not in classCount.keys() :classCount[value] = 0classCount[value] += 1 # 计数+1sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) # reverse=True降序排列  根据字典的值降序排序return sortedClassCount[0][0] # 返回数据最多的类别名称，由于采用降序排列，因此数组中[0][0]位置即为数据最多的类别
'''
2.函数说明:递归构建决策树
Parameters:dataSet - 训练数据集features - 分类属性标签featLabels - 存储选择的最优特征标签
Returns:myTree - 决策树
'''
def createTree(dataset,features) :# 取出样本中的所有类别标签classList = [example[-1] for example in dataset] # -1表示最后一个 是or否# 判断递归条件if classList.count(classList[0]) == len(dataset) : # 如果类别完全相同则达到递归终止条件 停止继续划分return classList[0]if len(dataset[0]) == 1 : # 遍历完所有的特征返回出现次数最多的类标签return majorityCnt(classList)bestFeat = chooseBestFeatureToSplit(dataset) # 调用自定义chooseBestFeatureToSplit方法，选择最优特征bestFeatLabel = features[bestFeat] # 获取最优特征的标签myTree = {bestFeatLabel : {}} # 根据最优特征的标签生成树 分类结果以字典的形式保存del(features[bestFeat]) # 当使用该属性完成划分后，该属性就无效了需要在features列表中将用过的属性删除featValues = [example[bestFeat] for example in dataset] # 通过for循环得到训练集中所有最有特征的属性值uniqueVals = set(featValues) # 去重操作 去掉重复的属性值for value in uniqueVals :subLabels = features[:] # 拷贝一个数据列表# 递归调用函数createTree,遍历特征，创建决策树myTree[bestFeatLabel][value] = createTree(splitDataSet(dataset,bestFeat,value),subLabels) # 对于每一个分支，需要通过递归创建树return myTreedataset,features = createDataset()
myTree = createTree(dataset,features)
print(myTree)
TreePlotter.createPlot(myTree)

TreePlotter.py

import matplotlib.pylab as plt
import matplotlib# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams[ 'font.serif'] = ['SimHei']# 分叉节点，也就是决策节点  创建字典
decisionNode = dict(boxstyle="sawtooth", fc="0.8")# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")# 箭头样式
arrow_args = dict(arrowstyle="<-")def plotNode(nodeTxt, centerPt, parentPt, nodeType):"""绘制一个节点:param nodeTxt: 描述该节点的文本信息:param centerPt: 文本的坐标:param parentPt: 点的坐标，这里也是指父节点的坐标:param nodeType: 节点类型,分为叶子节点和决策节点:return:"""createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)def getNumLeafs(myTree):"""获取叶节点的数目:param myTree::return:"""# 统计叶子节点的总数numLeafs = 0# 得到当前第一个key，也就是根节点firstStr = list(myTree.keys())[0]# 得到第一个key对应的内容secondDict = myTree[firstStr]# 递归遍历叶子节点for key in secondDict.keys():# 如果key对应的是一个字典，就递归调用if type(secondDict[key]).__name__ == 'dict':numLeafs += getNumLeafs(secondDict[key])# 不是的话，说明此时是一个叶子节点else:numLeafs += 1return numLeafsdef getTreeDepth(myTree):"""得到树的深度层数:param myTree::return:"""# 用来保存最大层数maxDepth = 0# 得到根节点firstStr = list(myTree.keys())[0]# 得到key对应的内容secondDic = myTree[firstStr]# 遍历所有子节点for key in secondDic.keys():# 如果该节点是字典，就递归调用if type(secondDic[key]).__name__ == 'dict':# 子节点的深度加1thisDepth = 1 + getTreeDepth(secondDic[key])# 说明此时是叶子节点else:thisDepth = 1# 替换最大层数if thisDepth > maxDepth:maxDepth = thisDepthreturn maxDepthdef plotMidText(cntrPt, parentPt, txtString):"""计算出父节点和子节点的中间位置，填充信息:param cntrPt: 子节点坐标:param parentPt: 父节点坐标:param txtString: 填充的文本信息:return:"""# 计算x轴的中间位置xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]# 计算y轴的中间位置yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]# 进行绘制createPlot.ax1.text(xMid, yMid, txtString)def plotTree(myTree, parentPt, nodeTxt):"""绘制出树的所有节点，递归绘制:param myTree: 树:param parentPt: 父节点的坐标:param nodeTxt: 节点的文本信息:return:"""# 计算叶子节点数numLeafs = getNumLeafs(myTree=myTree)# 计算树的深度depth = getTreeDepth(myTree=myTree)# 得到根节点的信息内容firstStr = list(myTree.keys())[0]# 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)# 绘制该节点与父节点的联系plotMidText(cntrPt, parentPt, nodeTxt)# 绘制该节点plotNode(firstStr, cntrPt, parentPt, decisionNode)# 得到当前根节点对应的子树secondDict = myTree[firstStr]# 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD# 循环遍历所有的keyfor key in secondDict.keys():# 如果当前的key是字典的话，代表还有子树，则递归遍历if isinstance(secondDict[key], dict):plotTree(secondDict[key], cntrPt, str(key))else:# 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/WplotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW# 打开注释可以观察叶子节点的坐标变化# print((plotTree.xOff, plotTree.yOff), secondDict[key])# 绘制叶子节点plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)# 绘制叶子节点和父节点的中间连线内容plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))# 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalDdef createPlot(inTree):"""需要绘制的决策树:param inTree: 决策树字典:return:"""# 创建一个图像fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)# 计算出决策树的总宽度plotTree.totalW = float(getNumLeafs(inTree))# 计算出决策树的总深度plotTree.totalD = float(getTreeDepth(inTree))# 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2WplotTree.xOff = -0.5 / plotTree.totalW# 初始的y轴偏移量，每次向下或者向上移动1/DplotTree.yOff = 1.0# 调用函数进行绘制节点图像plotTree(inTree, (0.5, 1.0), '')# 绘制plt.show()if __name__ == '__main__':print((matplotlib._fname()))testTree = {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}, 3: 'maybe'}}createPlot(testTree)