原始信号为基带模拟信号，要想在空气中传播信号，必须使用频带信号（频率高则天线长度降低，且可能进行频分复用等）
要产生频带信号，需要频谱搬移，这就是调制；基带信号经过调制，得到已调信号/调制信号/频带信号

模拟调制

模拟调制就是 用模拟信号去控制高频载波的幅度/频率/相位，对应AM/FM/PM
下面只讨论调幅AM

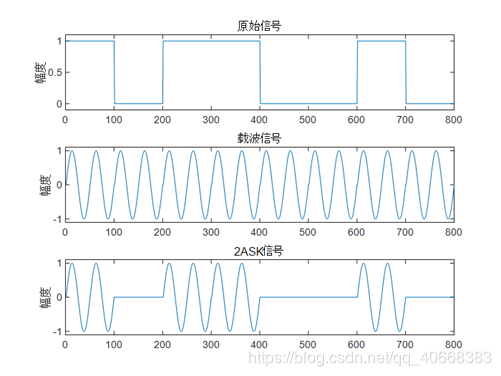
• 标准AM调幅：思路是 [从时域出发] 让已调信号的整体包络=要传输的模拟信号的波形

调制：模拟信号$x(t)$幅值可能为负，需要将电平整体抬高为$x(t)+A_0$，然后与高频载波$cos{\omega }_{c}t$相乘，已调信号为$s(t)=[x(t)+A_0]cos{\omega }_{c}t$
频谱：由于时域叠加了$A_0$，频域额外增加了两个位于载频的冲激，占用了一定的功率

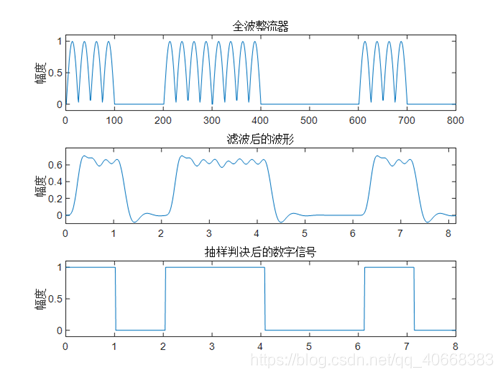
解调：很方便，二极管单向导通截取已调信号的正值部分，低通滤波得到包络波形，最后用电容的隔直流特性，将信号搬移回到零电平附近

特点：调制效率低，但可以使用非相干解调，实现简单成本低，用于无线电广播

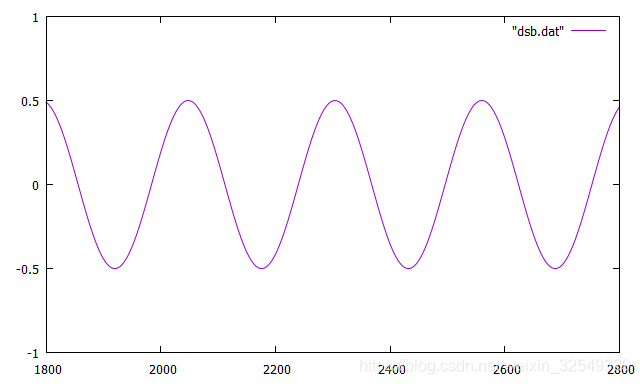
• 抑制载波双边带DSB-SC：不看时域，转而关注频谱，希望调制时不再分配功率给未携带信息的“空载波”

调制：$s(t)=x(t)cos{\omega }_{c}t$
解调：只能从频域角度入手，使用相干解调（频谱搬移）

• 单边带SSB：双边带调制中，上边带和下边带携带的信息是重复的（都包含完整信息），只需留下一个边带

调制：DSB之后进行LPF/HPF滤波，滤去一个边带
解调：相干解调

相干解调

非相干解调主要就是AM解调中的包络检测技术，优点在于低成本，不要求获得高频载波，但相比相干接收机，性能下降3dB；

相干解调基于频谱搬移思想，其核心在于载波恢复，即接收端需要获得与发射端相同频同相的高频正弦信号

载波恢复

从直观上看，载波恢复是有可能的：从接收信号（虚线表示）中的各个过零点可以获得载波的频率和相位，从而恢复载波信号（实线表示）

唯一的问题是，载波恢复存在$\pi$的相位模糊，这是调制信号特点决定的，用任何方法都无法避免
这个问题来源于接收信号和载波时而同相时而反相（反相：一个信号在波峰而另一个信号在波谷）

因此，恢复出来的载波可以移动相位$\pi$，或者说加一个负号

关键器件：锁相环

锁相环是载波恢复中的关键器件，由鉴相器（乘法器，积化和差）、环路滤波器（即LPF）和压控振荡器VCO组成

输入正弦信号，锁相环进入锁定状态后，可以输出一个与与参考信号同频且基本同相的正弦信号

锁相环原理

假设输入和输出信号分别为：$$s(t)=\cos \left(2\pi f_{c}t+\varphi \right)和c(t)=\sin \left(2\pi {\hat{f}}_{c}t+\hat{\varphi }\right)$$经过乘法器（积化和差）和环路滤波器（LPF留下积化和差的低频成分），得到 VCO控制电压$$u_c(t)=-\frac{1}{2}\sin \left[2\pi \left({\hat{f}}_c-f_c\right)t+\hat{\varphi }-\varphi \right]$$其中额外加了一个负号，负号是为了获得一个负反馈回路，一旦$f_c\ne {\hat{f}}_c$，$u_c(t)$就随时间变化（含有变量$t$），进而VCO输出频率${\hat{f}}_c$又不断改变；这就是说VCO能够跟踪输入信号频率，直到$f_c={\hat{f}}_c$VCO进入锁定状态，控制电压稳定为$$u_c(t)=\frac{1}{2}\sin (\varphi -\hat{\varphi })$$注意，不可能有$\varphi =\hat{\varphi }$，否则输出频率就是VCO的自由振荡频率（见后文），但其实$\varphi$和$\hat{\varphi }$的差异很小，如果VCO的控制灵敏度$K$很高，则只需很小的$\varphi -\hat{\varphi }$就能实现频率锁定（$f_c={\hat{f}}_c$）

综上：

• 输入正弦信号，锁相环进入锁定状态后，可以输出一个与与参考信号同频且基本同相的正弦信号（若输入参考信号的频率低于VCO的自由振荡频率，则输出与输入参考信号的相位差为正，否则为负）
• 锁相环具有负反馈回路，作用是锁定跟踪输入参考信号的频率和相位
  例如，当输出的相位$\hat{\varphi }$意外增大，则$u_c(t)=\frac{1}{2}\sin (\varphi -\hat{\varphi })$减小，从而输出信号的瞬时角频率减小，频率变低等价于 「与原有角频率相比，相位减小」，最终达到修正和“锁定”相位的效果

压控振荡器VCO

压控振荡器VCO的输出是一个正弦信号，且能够通过输入的电压控制输出的正弦信号的频率

VCO的原理：基于LC谐振电路能够起振并输出一个正弦波，并且正弦波的频率由电感和电容决定；而VCO就是用外加电压控制电容值（这种特殊的“电容”就是变容二极管），从而用电压控制电路的谐振频率
VCO的特性如下，横轴为输入的控制电压$u_c$，纵轴为输出的正弦信号的角频率；

其中$u_c=0$时的角频率${\omega }_{0,0}=2\pi f_0$为自由振荡角频率，$u_c=0$处的斜率$K$为控制灵敏度

VCO的输出正弦信号为：$$c(t)=\cos [\theta (t)],相位\theta (t)=2\pi f_{0}t+K{\int }_{-\infty }^t{u}_c(\tau )\mathrm{d}\tau$$输出信号的瞬时角频率为$$\omega (t)=\frac{\mathrm{d}}{\mathrm{d}t}\theta (t)=2\pi f_0+K{u}_c(t)$$

• 这就是说，VCO的瞬时角频率$\omega$与控制电压$u_c$成线性关系
  当$u_c=0$，输出自由振荡频率$2\pi f_0$，当$u_c=v$，输出自由振荡频率$2\pi f_0+Kv$
• 并且，无论$u_c(t)$波形如何，由于积分作用，相位$\theta (t)$必然是连续的，进而输出波形$c(t)$必然是连续的

VCO的应用广泛，例如可以实现连续相位的调频信号

载波恢复技术：平方环

首先将接收信号$s(t)$平方处理（积化和差）并BPF滤波，得到二倍频的载波$\cos \left(4\pi f_{c}t+\varphi \right)$，用它驱动锁相环得到$\sin \left(4\pi f_{c}t+2\hat{\varphi }\right)$，再做二分频和90°相移得到余弦载波$\cos \left(2\pi f_{c}t+\varphi \right)$
左下角则是相干解调的部分

为什么要用锁相环？
因为平方处理并BPF滤波得到的$\cos \left(4\pi f_{c}t+\varphi \right)$并不是纯粹的正弦波，而是混入了数据信息和噪声（BPF不能做到很高的Q值，从而预留一定宽度来容纳发射机的载波频率漂移），使用锁相环则能过输出较为“干净”的载波（数据信息相对于载波是慢变信号，对锁相环影响不大，并且经过锁相环后噪声也很小）

载波恢复技术：Costas环

Costas环结构简单，可以直接输出解调后的信号$s(t)$

假设VCO的输出与载频同频但相位略有不同，即为$\sin \left(2\pi f_{c}t+\hat{\varphi }\right)$，那么有：$$v_1(t)=\frac{s(t)}{2}\cos (\hat{\varphi }-\varphi )和v_2(t)=\frac{s(t)}{2}\sin (\hat{\varphi }-\varphi )$$则鉴相器（积化和差）的输出为$$e(t)=\frac{s^2(t)}{8}\sin (2\hat{\varphi }-2\varphi )$$后续的原理如VCO部分所述，最终可以实现VCO的锁定

变频/混频技术

变频 / 也称混频 就是频谱的搬移（不改变频谱形状的单纯搬移）

理论上就是一个乘法器实现：DSB中的$s(t)=x(t)cos{\omega }_{c}t$和IQ调制中的$s(t)=x(t)cos{\omega }_{c}t-y(t)sin{\omega }_{c}t$，都是在变频，这称为直接变频

然而实际中，可能由于实现难度高，需要间接变频：即基带信号先调制到中频IF，再变换为射频载波RF

基带到中频信号（就是一个IQ调制，调制到中频）：${\mathrm{s}}_{IF}(\mathrm{t})=\mathrm{I}(\mathrm{t})\cos {\omega }_{IF}\mathrm{t}-\mathrm{Q}(\mathrm{t})\sin {\omega }_{IF}\mathrm{t}$

中频到射频（就是一个混频过程，将载波频率从中频变为射频）：$$\begin{array}{rl}{s}_{\mathrm{RF}}^{\prime }(t)& =\left[I(t)\cos {\omega }_{\mathrm{IF}}t-Q(t)\sin {\omega }_{\mathrm{IF}}t\right]\cos {\omega }_{\mathrm{L}}t\\ & =\frac{1}{2}I(t)\left[\cos \left({\omega }_{\mathrm{L}}+{\omega }_{\mathrm{IF}}\right)t+\cos \left({\omega }_{\mathrm{L}}-{\omega }_{\mathrm{IF}}\right)t\right]-\frac{1}{2}Q(t)\left[\sin \left({\omega }_{\mathrm{L}}+{\omega }_{\mathrm{IF}}\right)t-\sin \left({\omega }_{\mathrm{L}}-{\omega }_{\mathrm{IF}}\right)t\right]\end{array}$$
HPF滤波器滤除低频： s R F ( t ) = H P F { s R F ′ ( t ) } = I ( t ) cos ⁡ ( ω I F + ω L ) t − Q ( t ) sin ⁡ ( ω I F + ω L ) t s_{\mathrm{RF}}(t)=HPF\{s_{\mathrm{RF}}^{\prime}(t)\}=I(t) \cos( \omega_{IF}+\omega_{L}) t-Q(t) \sin ( \omega_{IF}+\omega_{L})t sRF​(t)=HPF{sRF′​(t)}=I(t)cos(ωIF​+ωL​)t−Q(t)sin(ωIF​+ωL​)t

最终得到了载波位于${\omega }_{RF}={\omega }_{IF}+{\omega }_L$的频带信号

实际中，基带信号是数字信号，基带到中频的上/下变频都使用数字信号处理实现（数字上变频器DUC和数字下变频器DDC）