相关系数（Correlation coefficient）可用于评估两个变量之间的线性关系，它的值在-1到1之间，-1或1代表完美的负相关和正相关，0表示不存在线性关系。
计算相关系数的方法种类繁多，各有自己的定义以及适用情况
面对相同的数据，如果采用不同的相关分析，会得出不同的相关系数，如下图：
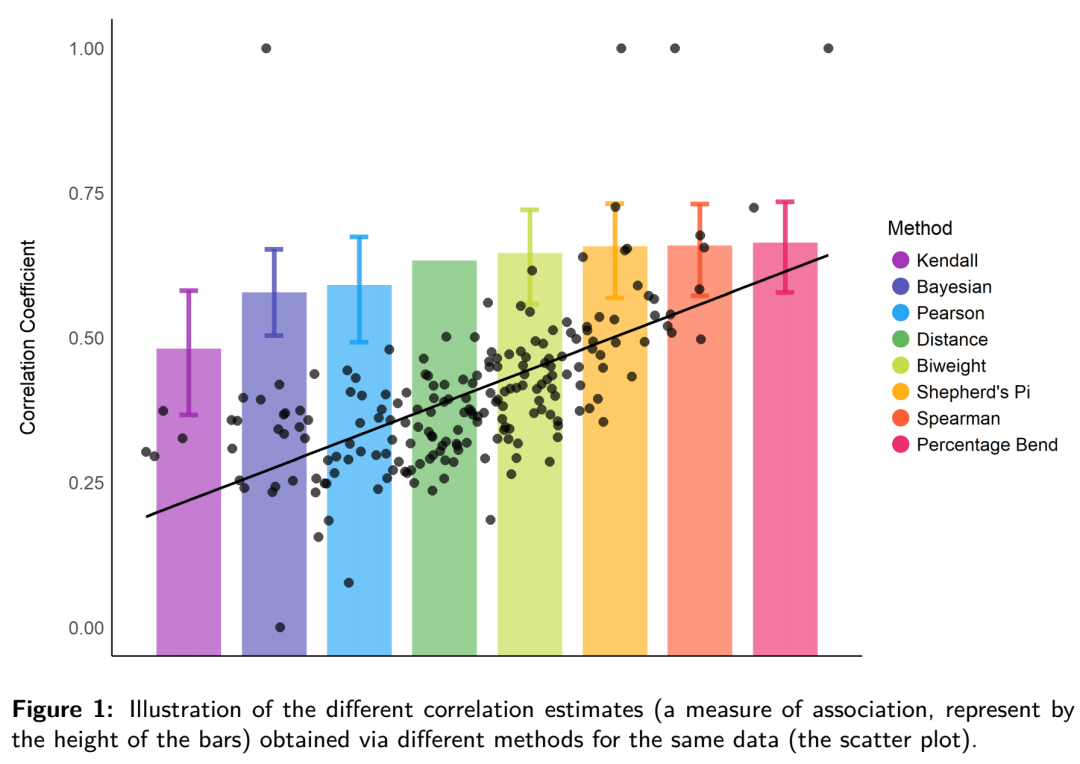
图片来源： [1]
一般来说，如果没有特别注明，我们所说的相关系数，通常指的是Pearson'r，由Pearson相关（Pearson’s correlation）计算得出。
不夸张的说，Pearson相关很可能是统计中被使用次数最多的方法。但它的使用也有诸多限制，比如两个变量需为连续变量，呈线性关系，无明显的极值，以及正态分布等。
第二种常见的相关分析方法应该是Spearman相关（Spearman's correlation），是一种非参数检验，受到的限制相对较少，可用于非正态分布的变量。
其实，掌握上述两种方法应该可以解决90%+以上的相关分析问题！
但是，小编接下来将会介绍15种相关分析算法的实操代码，助你在“相关分析”这个领域，可以“一览众山小”
马上进入操作部分
首先，安装R包{correlation}:
接下来使用R自带的数据集“iris”作为实战演练的例子，想要使用Pearson相关计算“iris”的各个变量之间的相关系数，并且计算它们的95%置信区间，以及p值。
那该怎么办？
代码简单的有点恐怖
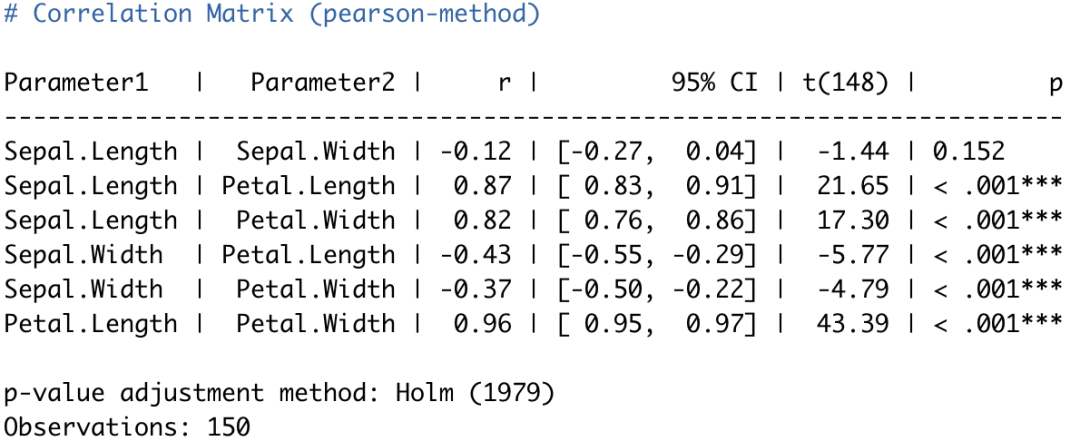
输出结果非常的简洁明了！
correlation()在默认情况下，将“iris”中的非连续变量“Species”剔除，只将其他四个连续变量分别进行两两的相关分析，使用的方法为Pearson相关，p值的计算使用了Holm(1979)方法进行多重校正。
此外，也可以采用不同的呈现结果的方法：
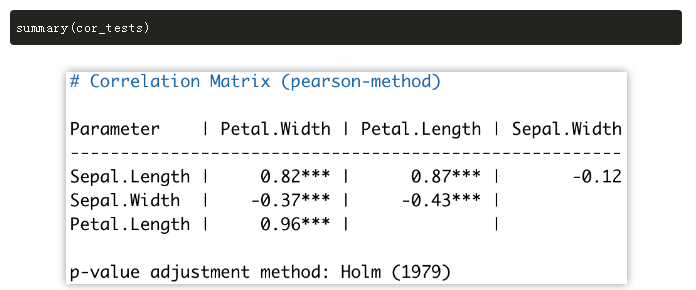
那如何进行分组别的相关分析？
即在不同Species组别中进行相关分析，可以这么做：
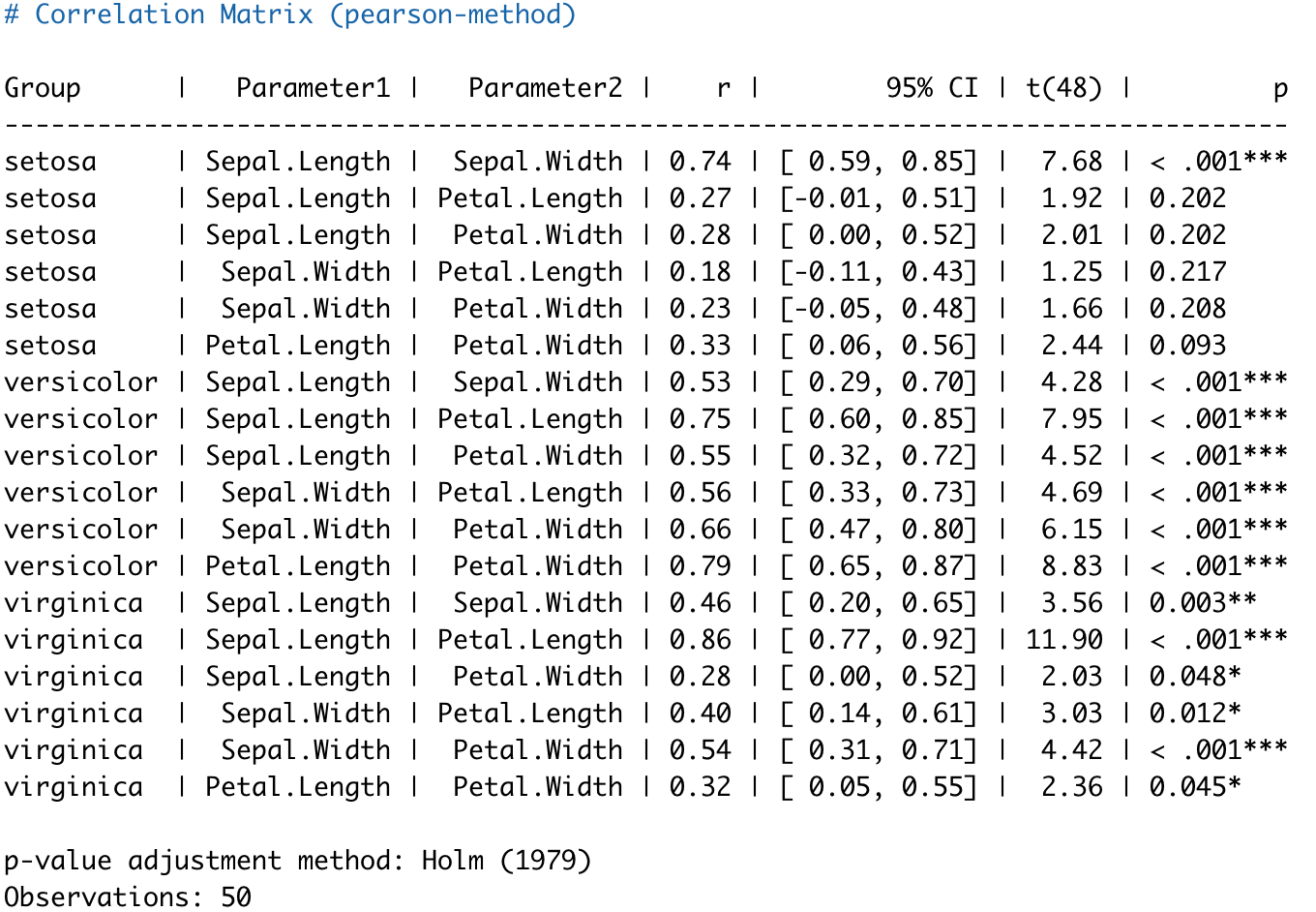这非常实用
除默认的Pearson相关外，correlation()共含有以下相关分析：
-
Pearson's correlation （默认）
-
Spearman's rank correlation
-
Kendall's rank correlation
-
Biweight midcorrelation
-
Distance correlation
-
Percentage bend correlation
-
Shepherd's Pi correlation
-
Blomqvist' coefficient
-
Hoeffding's D
-
Gamma correlation
-
Gaussian rank correlation
-
Point-Biserial and biserial correlation
-
Polychoric correlation
-
Tetrachoric correlation
-
Auto （根据数据自动选择）
与上述相关方法相对应的R中代码字符如下，只需要选取对应的代码既可以进行想要的相关分析
-
"pearson"
-
"spearman"
-
"kendall"
-
"biweight"
-
"distance"
-
"percentage"
-
"shepherd"
-
"blomqvist"
-
"hoeffding"
-
"gamma"
-
"gaussian"
-
"biserial"
-
"polychoric"
-
"tetrachoric"
-
"auto"
如果想要更加详细的了解上述的相关分析方法，可以?correlation查看帮助文档，见下图：
以使用spearman相关为例，只要将代码改为 method = "spearman" 即可使用：
好啦，今天的内容就到这里，感兴趣的小伙伴可以参考以下文献深入学习[1][2]。
如果有帮助，记得分享给需要的人
参考文献
[1]. Makowski et al., (2020). Methods and Algorithms for Correlation Analysis in R.
[2]. https://easystats.github.io/correlation/index.html
人工智能 大气环境 气象水文 土壤地下水视频教程汇总
https://mp.weixin.qq.com/s?__biz=MzUzMTczMDMwMw==&mid=2247500552&idx=4&sn=0d68a31fcdac77b47f1aec2c04e65f78&chksm=fabc9918cdcb100e706da62a720d2343106238ca2fc4a4aac001bad3e01d066d1355284fa6bd&token=1940394883&lang=zh_CN#rd
