利用MATLAB生成软件二阶低通滤波器

`=================================================
嵌入式的软件滤波中，除了均值和限幅，我们常用的也就是一阶或者二阶，这些都是可以通过c语言代码来实现的。其过程包括分母A和分子B参数的求取，再者通过公式得出想要的输出结果。

文章目录

利用MATLAB生成软件二阶低通滤波器
一、一阶巴特沃斯低通滤波器设计
二、二阶巴特沃斯低通滤波器设计
三、IIR滤波器的差分方程
总结

一、一阶巴特沃斯低通滤波器设计

第一步：其参数A和B的求取可以通过Matlab的滤波器工具箱
来获得（因为这个c语言代码还不知道怎么写出来），打开Matlab软件，依次Start(在Matlab界面的左下角)->Toolboxes->Filter Design->Filter Design & Analysis Tool (fdatool)，打开的界面如下：
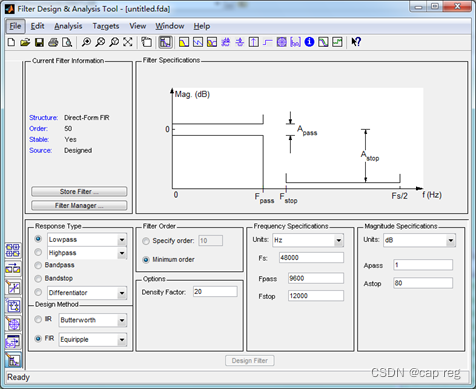
在这里插入图片描述
可以针对自己想要的滤波器，这里都可以进行设置，得到相应的参数，本人需要一阶巴特沃斯低通滤波器，采样频率：250Hz，截止频率5Hz，设置如下：

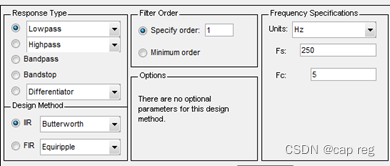
在这里插入图片描述
然后，点Design Filter即可，接着在菜单栏Analysis->Filter Coefficients，可以看到分母A和分子B相应的参数：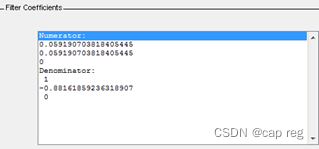
第二步：参数得到，代入公式即可了。
差分方程公式为：

xt 为当前输入，c语言代码为：

float  LOW_PASS_FILTER1ORDER(float curr_input)
{static  float  input[2];static  float  output[2];/*获取最新输入*/input[1] = curr_input;/* Butterworth */output[1] =B[0] * input[1] +B[1] * input[0] - A[1] * output[0];/* 输入序列保存 */input[0] = input[1];/*输出序列保存 */output[0] = output[1];return output[1];
}

二、二阶巴特沃斯低通滤波器设计

第一步：二阶的话，其用Matlab获取参数和c语言代码得到参数都可以，Matlab获取参数跟上述类似，如下图所示：
第一步设置FS和FC并生成滤波器：
在这里插入图片描述
生成滤波器后，电机左上角的[b，a]选项模块

第三步，点击edit->convert to single section 获得bk和ak

最后：

其中，Numerator，分子，也就是传递函数中的b项们，从上到下依次为b0、b1、b2。
Denominator，分母，也就是传递函数中的a项，从上到下依次为a0、a1、a2，其中a0总是为1。
除了上述方法，现在使用c语言代码得到分子B和分母A的参数。
设置采样频率为fs，截止频率为fc，则：
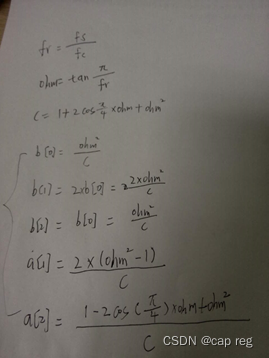
在这里插入图片描述
其公式的代码展示为：


/**************************************************
通过此函数可以得到二阶巴特沃斯的系数
****************************************************/
void  Lowpassfilter2orderSetCutoffFreq(float sample_freq, float cutoff_freq)
{float fr =0;  float ohm =0;float c =0;fr= sample_freq/cutoff_freq;ohm=tanf(M_PI_F/fr);c=1.0f+2.0f*cosf(M_PI_F/4.0f)*ohm + ohm*ohm;//    _cutoff_freq1 = cutoff_freq;
//    if (_cutoff_freq1 > 0.0f) 
//		{b_acc[0] = ohm*ohm/c;b_acc[1] = 2.0f*b_acc[0];b_acc[2] = b_acc[0];a_acc[1] = 2.0f*(ohm*ohm-1.0f)/c;a_acc[2] = (1.0f-2.0f*cosf(M_PI_F/4.0f)*ohm+ohm*ohm)/c;
//		}
}

第二步：代入公式
一个二阶结构是这样的一个表达式：

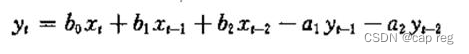
在这里插入图片描述
这个表达式中需要过去的4个历史值： Xt-1,Xt-2,Yt-1,Yt-2
二阶的意思就是：输入和输出项最多用到过去两个阶段的历史值，要用static来描述过去的变量和过去的过去的变量。
C代码的实现如下（已验证，得到了实现）：

float  LowPassfilter2order(float curr_input)
{static  float  input[3];static  float  output[3];/*获取最新输入*/input[2] = curr_input;/* Butterworth */output[2] =B[0] * input[2] +B[1] * input[1] +B[2] * input[0] - A[1] * output[1] - A[2] * output[0];/* 输入序列保存 */input[0] = input[1];input[1] = input[2];/*输出序列保存 */output[0] = output[1];output[1] = output[2];return output[2];
}

有一个简单的技巧，可以把上面的计算简化，使得历史状态由4减为2，定义下面的表达式：

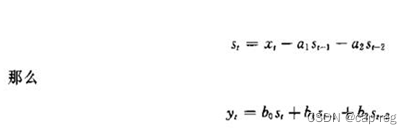
在这里插入图片描述
那么代码就可以写为：

/******************************************
二阶巴特沃斯低通滤波函数
*******************************************/
static float           _delay_element_11;        // buffered sample -1
static float           _delay_element_21;        // buffered sample -2float  LowPassfilter2order(float sample)
{float delay_element_0 = 0, output=0;delay_element_0 = sample - _delay_element_11 * a_acc[1] - _delay_element_21 * a_acc[2];if (isnan(delay_element_0) || isinf(delay_element_0)) {// don't allow bad values to propogate via the filterdelay_element_0 = sample;}output = delay_element_0 * b_acc[0] + _delay_element_11 * b_acc[1] + _delay_element_21 * b_acc[2];_delay_element_21 = _delay_element_11;_delay_element_11 = delay_element_0;// return the value.  Should be no need to check limitsreturn output;
//		}
}

两种方法都可使用哦，看个人的选择。

三、IIR滤波器的差分方程

那有的朋友就问了，这个滤波器方程是从哪来的呢，当初我也有这个疑问。

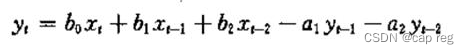
在这里插入图片描述
这个方程是如何得出的呢，通过如下的图片可以给出解答（down别人的）：

上面的方程是通过IIR差分方程的直接型得出的。
具体的解释为：

首先，当一个系统的输入为冲激函数时，它的输出即为冲激响应。
IIR(Infinite impulse response)&FIR(Finite impulse response)
(1)IIR(无限冲激响应)型数字滤波器顾名思义，当输入为冲激函数时，输出冲激响应h[n]（由于属于数字滤波器，自变量变为n）可以无限延长。(2)FIR(有限冲激响应)型数字滤波器当输入为冲激函数时，输出冲激响应 h[n] 可以在有限的时间长内结束。造成这种现象的主要原因是因为IIR型的滤波器采用了递归的结构，即结构中存在回环形成反馈支路来不断地产生输入以进行无限的输出；与之相比，FIR滤波器则实现的较为简单，它的结构中不存在反馈部分，因此它的冲激响应是有限的。

所以，利用左上角的差分方程带入相应的阶数k即可得到所需要的C语言函数方程了。