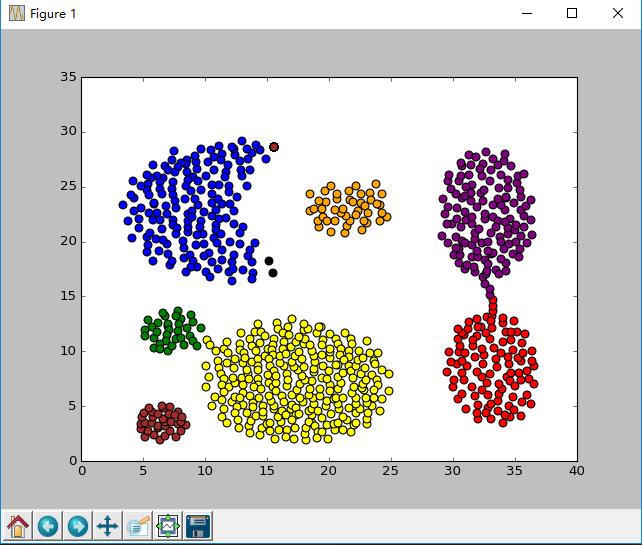
DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法，和 K-Means，BIRCH 这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。下面我们就对DBSCAN算法的原理做一个总结。

基于密度的聚类算法主要的目标是寻找被低密度区域分离的高密度区域。与基于距离的聚类算法不同的是，基于距离的聚类算法的聚类结果是球状的簇，而基于密度的聚类算法可以发现任意形状的聚类，这对于带有噪音点的数据起着重要的作用。

密度聚类原理

DBSCAN(Density-Based Spatial Clustering of Application with Noise)是一种典型的基于密度的聚类算法，在DBSCAN算法中将数据点分为一下三类：

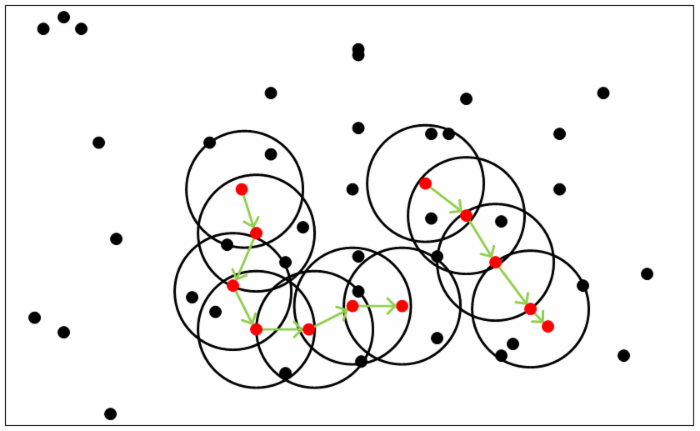
核心点。在半径 Eps 内含有超过 MinPts 数目的点

边界点。在半径 Eps 内点的数量小于 MinPts，但是落在核心点的邻域内

噪音点。既不是核心点也不是边界点的点

在这里有两个量，一个是半径 Eps，另一个是指定的数目 MinPts。

Eps 邻域。简单来讲就是与点

的距离小于等于 Eps 的所有的点的集合，可以表示为

。

直接密度可达。如果

在核心对象

的 Eps 邻域内，则称对象

从对象

出发是直接密度可达的。

密度可达。对于对象链：

，

是从

关于 Eps 和 MinPts 直接密度可达的，则对象

是从对象

关于 Eps 和 MinPts 密度可达的。

与 K-means 算法比起来，不需要预先输入划分的聚类个数。

聚类形成的簇的形状可以是任意的。

可以在需要的时候输入过滤噪声的参数。

DBSCAN 算法的聚类过程：

初始状态，给出一个数据集 D，并设置半径ε和 MinPts，将 D 中的所有对象标记为”unvisited”(未被访问)

随机从 D 中选取一个未被访问的对象 p，并标记为”visited”(已被访问)，检查 p 的ε-邻域内是否至少包含 MinPts 个对象(即 p 是否是核心对象)，若不是，则将 p 标记为噪声点，否则，为 p 创建一个新的簇 C，把 p 的ε-邻域中所有对象放入候选集合 N 中，并迭代的将 N 中不属于其它簇的对象加入到新簇 C 中，在这个过程中，将 N 中的”unvisited”的对象 q 标记为”visited”，若 q 的ε-邻域是否至少包含 MinPts 个对象，则将 q 的ε-邻域中所有的对象加入到 C 中，直到 C 不再扩大，N 为空的时候，此时簇 C 完成聚类，并输出。

继续从 D 中随机选取未被访问的对象 s，同样使用(2)中的聚类方法，直到对象集 D 中所有对象都被访问。

下面是该算法的伪代码：

算法：DBSCAN，一种基于密度的聚类算法 输入： D:包含若干个对象的数据集 ε:半径 MinPts:密度邻域阈值 输出：簇的集合 方法： 1.标记 D 中所有的对象为"unvisited"; 2.Do 3.随机选择一个"unvisited"对象 p; 4.标记 p 为"visited"; 5.If p 的ε-邻域至少含有 MinPts 个对象 6. 创建一个新的簇 C; 7. 令 N 为 p 的ε-邻域对象的集合; 8. For N 中的每个对象 q 9. If q 是"unvisited" 10. 则标记 q 为"visited"; 11. If q 是核心对象 12. 则将 q 的ε-邻域中的所有对象集合加到 N 中; 13. If q 不属于其它簇 14 则将 q 加入到簇 C 中; 15. End For; 16. 输出 C 17.Else 标记 p 为噪声点 18.Until D 中所以对象都是"visited"

【注：本文源自网络文章资源，由站长整理发布】

web 前端中文站 , 版权所有丨如未注明 , 均为原创丨本网站采用BY-NC-SA协议进行授权

转载请注明原文链接：聚类(DBSCAN)算法原理