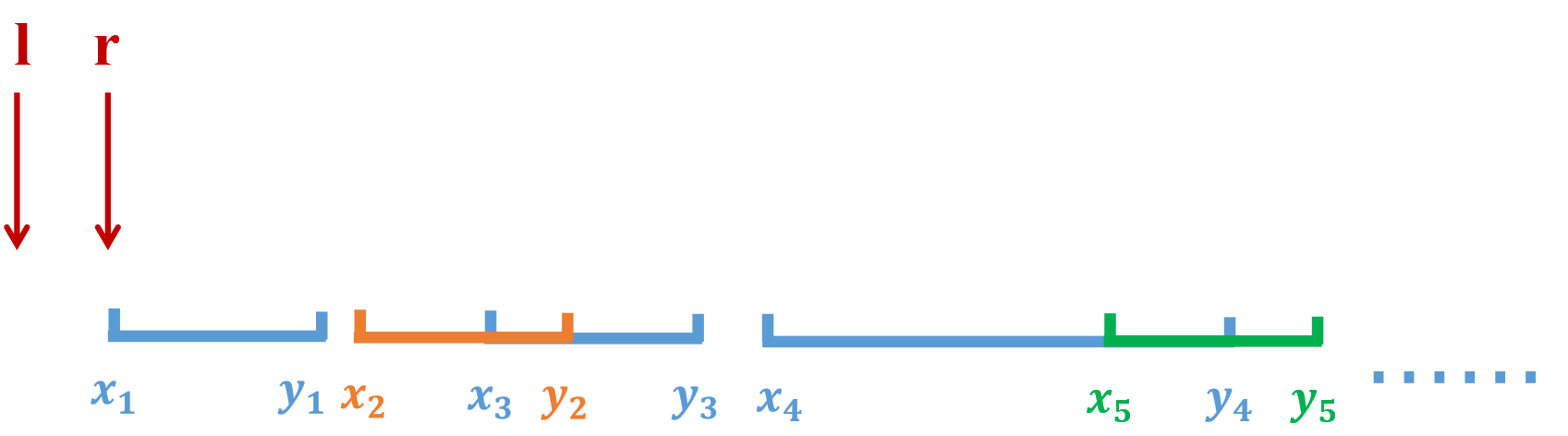莫队算法（普通莫队、带修莫队、树上莫队、不删除莫队）学习笔记【理解+套路/核心代码+例题及题解】

article/2025/10/24 4:33:03

一、理解

我的理解就是巧妙的暴力，利用双指针以及分块思想，巧妙的移动双指针，时间复杂度可以达到O(NlogN)。

强推博客：写的又好又全。链接

二、套路

1、普通莫队

【1】核心代码

bool cmp(node a,node b){return belong[a.l]==belong[b.l]? a.r<b.r:belong[a.l]<belong[b.l];
}	
sort(q+1,q+1+m,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){int ql=q[i].l,qr=q[i].r;while(l<ql) del(l++);while(l>ql) add(--l);while(r<qr) add(++r);while(r>qr) del(r--);	ans[q[i].id]=cnt;
}

add和del函数随机应变，一般都是加入或删除一个数对答案的影响。证明一下复杂度吧，便于理解代码。

（1）对左指针L，假设一个块内有x个询问，每次L最多移动 $\sqrt{n}$ 次，加起来为 $O(\sum{x\sqrt{n}}) = O(m\sqrt{n})$ ；对于不同块之间的L，跨越一个块L最多移动 $\sqrt{n}$ 次，总共可能跨n次，为 $O(n\sqrt{n}})$ 。

（2）对于右指针R，对于不同块之间的R，它是无序的，最多移动n次，有 $\sqrt{n}$ 块，为 $O(n\sqrt{n})$ ；块内的R有序，R最多移动 $\sqrt{n}$ 次，总共 $\sqrt{n}$ 块，为 $O(n)$ 。

因此总体为 $max( O(m\sqrt{n}) , O(n\sqrt{n}))$ ，有常数。

【2】例题及题解（从易到难）

（1）luogu SP3267 DQUERY - D-query 题解

（2）luogu P1972 [SDOI2009]HH的项链题解

（3）luogu P2709 小B的询问题解

（4） CodeForces - 86D Powerful array 题解

（5）luogu P1494 [国家集训队]小Z的袜子题解

（6）luogu P3709 大爷的字符串题题解

（7）CodeForces - 617E XOR and Favorite Number 题解

2、带修莫队

【1】核心代码

bool cmp(node a,node b){return (be[a.l]^be[b.l])?be[a.l]<be[b.l] :(be[a.r]^be[b.r]) ? be[a.r]<be[b.r] : a.tim<b.tim;
}
blcok=ceil(pow(1.0*n,2.0/3.0));//注意这里要变为n^(2/3) 
int l=1,r=0,ti=0;
while(l<ql) del(l++);
while(l>ql) add(--l);
while(r<qr) add(++r);
while(r>qr) del(r--);
while(ti<qt){++ti;if(ql<=b[ti].pos&&b[ti].pos<=qr)del(b[ti].pos);swap(a[b[ti].pos],b[ti].col);if(ql<=b[ti].pos&&b[ti].pos<=qr)add(b[ti].pos);
}
while(ti>qt){if(ql<=b[ti].pos&&b[ti].pos<=qr)del(b[ti].pos);swap(a[b[ti].pos],b[ti].col);if(ql<=b[ti].pos&&b[ti].pos<=qr)add(b[ti].pos);--ti;
}

对于带修莫队，我们需要给每一个询问加一个时间戳，时间戳的取值就是之前最近的修改。排序时，先按左边界的块，再按右边界的块，最后按时间戳。先移动左右指针，然后再考虑修改。

如果时间戳大了，说明我们改多了，我们需要再改回去，改的时候，要考虑是否对答案造成影响；

如果时间戳小了，说明我们改少了，要改到询问所在的时间戳，改的时候，要考虑是否对答案造成影响。

使用swap可以方便地进行修改。（具体看上面代码）

注意：有的dalaodalao证明了当块的大小设 $n^{\frac{3}{4}}$ 时理论复杂度达到最优。不过可以证明，块大小取 $n^{\frac{2}{3}}$ 优于取 $\sqrt{n}$ 的情况，总体复杂度 $O(n^{\frac{5}{3}})$ 。而块大小取 $\sqrt{n}$ 时会退化成 $O(n^{2})$ ，不建议使用。（出处）

【2】例题及题解

（1）luogu P1903 [国家集训队]数颜色 / 维护队列题解

（2）HDU - 6610 Game 题解

（3）luogu P4074 [WC2013]糖果公园【树上带修莫队有难度】题解

3、树上莫队

【1】核心代码

bool cmp(Node a,Node b){return (be[a.l]^be[b.l]) ? be[a.l]<be[b.l] : (be[a.l]&1) ? a.r<b.r : a.r>b.r;
}
int fir[N],la[N],dfn[N<<1],tot=0;
int dep[N],f[N][30]; 
void dfs(int u,int fa){fir[u]=++tot;dfn[tot]=u;for(int i=1;i<=20;++i)f[u][i]=f[f[u][i-1]][i-1];for(int i=head[u];~i;i=g[i].nex){int v=g[i].to;if(dep[v]||v==fa) continue;dep[v]=dep[u]+1;f[v][0]=u;dfs(v,u);}la[u]=++tot;dfn[tot]=u;
}
int getLca(int x,int y){if(dep[x]<dep[y]) swap(x,y);int dis=dep[x]-dep[y];for(int i=20;i>=0;--i)if(dis&(1<<i))x=f[x][i];if(x==y) return x;for(int i=20;i>=0;--i)if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i]; return f[x][0];
}
void change(int x){x=dfn[x];vis[x] ? del(x) : add(x);vis[x]^=1;
}
for(int i=1;i<=m;++i){int u,v;//scanf("%d%d",&u,&v);u=read(),v=read();if(fir[u]>fir[v]) swap(u,v);int lca=getLca(u,v);if(lca==u)q[i].l=fir[u];elseq[i].l=la[u],q[i].lca=lca;;q[i].r=fir[v];q[i].id=i;
}	
sort(q+1,q+1+m,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++){int ql=q[i].l,qr=q[i].r,lca=q[i].lca;	while(l<ql) change(l++);while(l>ql) change(--l);while(r<qr) change(++r);while(r>qr) change(r--);ans[q[i].id]=sum;if(lca && !num[a[lca]]) ++ans[q[i].id];		
}

这里需要了解欧拉序（强推博客），利用欧拉序，就可以把树上的路径转化为连续区间的问题。

这里还要求lca。对于树上u到v的路径，设first[u]<first[v]，

如果lca(u,v)==u，对应欧拉序的连续区间就为[ first[u] , first[v] ] ;

否则，对应欧拉序的连续区间就为[ last[u] , first[v] ] , 不过还要加上 lca(u,v) 。

要注意的是区间中出现两次的点并不在u到v的路径中，所以我们需要一个vis数组，每次进行异或操作。根据vis[i],进行删除操作/添加操作。

一定记得有的数组需要开2*n并且别忘了加lca的贡献 !!!!!!!!

【2】例题及题解

（1）luogu SP10707 COT2 - Count on a tree II 题解

（2）luogu P4074 [WC2013]糖果公园【树上带修莫队有难度】题解

4、不删除莫队

【1】核心代码

bool cmp(node a,node b){return (be[a.l]^be[b.l]) ? be[a.l]<be[b.l] : a.r<b.r;
}
block=ceil(sqrt(1.0*n));
bnum=ceil(1.0*n/block);
for(int i=1;i<=bnum;i++){bl[i]=br[i-1]+1,br[i]=br[i-1]+block;for(int j=bl[i];j<=br[i];j++)be[j]=i;
}
for(int i=1;i<=m;i++)scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
sort(q+1,q+1+m,cmp);
int pos=1;
ll sum;
for(int i=0;i<=bnum;i++){sum=0;memset(cnt,0,sizeof cnt);int l=br[i]+1,r=br[i];for(;be[q[pos].l]==i;pos++){int ql=q[pos].l,qr=q[pos].r;if(be[ql]==be[qr]){ll temp=0;for(int j=ql;j<=qr;j++) cnt1[mp[a[j]]]=0;for(int j=ql;j<=qr;j++){++cnt1[mp[a[j]]];temp=max(1LL*a[j]*cnt1[mp[a[j]]],temp) ;}ans[q[pos].id]=temp;				continue;}while(r<qr){++r;++cnt[mp[a[r]]];sum=max(sum,1LL*a[r]*cnt[mp[a[r]]]); }ll temp=sum;while(l>ql){--l;++cnt[mp[a[l]]];sum=max(sum,1LL*a[l]*cnt[mp[a[l]]]); 				}ans[q[pos].id]=sum;while(l<br[i]+1){--cnt[mp[a[l]]];l++;}sum=temp;}
}

对于普通莫队，我们一般考虑添加和删除只是顺序变一下，但有的题删除操作根本没办法维护需要的东西。

这时，不删除莫队就可以大显神威了，删除太难了，那我们不删除，只添加就好了。

现在考虑怎么不删除，我们排序时，对于左端点在同一个块内的询问他们的r是从小到大有序的，那么我们可以利用这个特点，一个块一个块的计算询问区间。

对于左端点在同一个块内的询问：

首先考虑，如果询问区间的左右端点（ql、qr）都在一个块内，那我们直接暴力计算，复杂度为 $O(\sqrt{n})$ ，最多m个询问区间的左右端点（ql、qr）都在一个块内，复杂度为 $O(m\sqrt{n})$ 。