莫队算法

莫队算法是由前国家队莫涛提出的一种算法，主要应用在一类离线区间查询的问题中，同时具有多种扩展的应用，其主要思想是分块。

引例：给出一个序列，每次给定询问 $[l, r]$ ，求 $[l, r]$ 的区间和。（使用莫队来做，不用前缀和）

假定序列如下：

3 8 1 2 7 4 9 0 6

已知 $[2, 5]$ 区间和为 $18$ ，求 $[2, 6]$ 区间，你会怎么做？很简单 $18 + 4 = 22$

同理 $[2, 4]$ 的区间和呢？ $18 - 7 = 11$

于是乎 $[3, 6]$ 的区间和就可以用 $[2, 5]$ 减去第二项，加上第六项即可…

对于当前区间 $[l, r]$ ，可分为以下四种情况

加上 $l$ 左边一格的贡献： add(--l) ( $l$ 模拟指针)
加上 $r$ 右边一格的贡献： add(++r)
减去 $[l, r]$ 最左边一格的贡献： sub(++l)
减去 $[l, r]$ 最右边一格的贡献： sub(r--)

假定对于一个 $n$ 项的数列，询问以下 $m$ 次：

$[1, 2]$ $[n - 1, n]$ $[1, 2]$ $[n - 1, n]$ $[1, 2]$ $[n - 1, n]$ $. . .$

如果按照上述方式，比较区间之间的不同，每一次移动一个位置，复杂度将会升级到 $O (m n)$

但是，如果将询问顺序变一下：

$[1, 2]$ $[1, 2]$ $[1, 2]$ $[n - 1, n]$ $[n - 1, n]$ $[n - 1, n]$ $. . .$

复杂度就会变成 $O (m + n)$

因此很容易发现，询问的顺序直接影响了时间复杂度

普通莫队方法：

莫队算法解决的是区间的问题，其思想是将两个指针 $l$ , $r$ 进行移动，使得这两个指针覆盖到每一次查询的左右端点上，并且在移动过程中，计算他们的贡献。通过对一系列的询问进行排序，让这样移动的次数尽可能少，从而进行优化，这是一种偏向暴力的算法。

例如： $n$ 个数字，给定 $m$ 个询问，每次询问区间 $x_i, y_i]$ 的内容。做法是构造一个区间 $[l, r]$ ，移动端点 $l, r$ ，使其覆盖到每一个 $x_i, yi]$ ，并且计算答案。

1、分块：每一块的大小 $\sqrt n$
2、对所有询问进行排序， $[l, r]$ ，先按照左端点排序， $l$ 相同的则按照右端点排序，记录下答案，按照原顺序输出答案即可。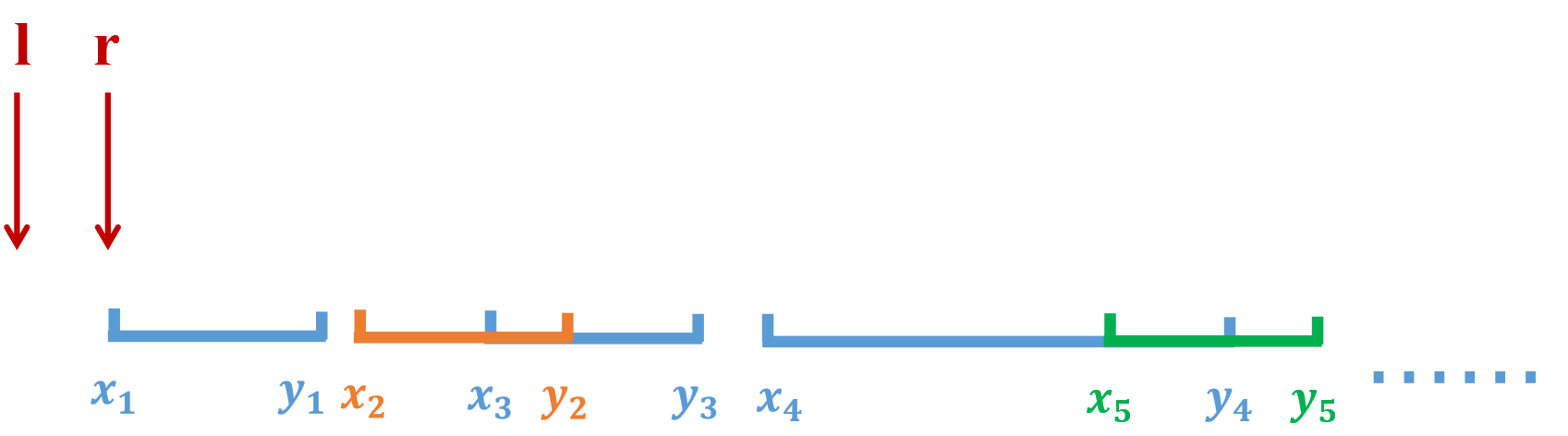

主要代码结构：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int N = 1e6 + 10;int a[N];
int pos[N];
int ans[N];
int res; // 维护当前[l,r]的值 struct Query {int l, r, k;
}q[N];int main () {int n, m;cin >> n >> m;int t = sqrt (n);for (int i = 1; i <= n; i ++) {	cin >> a[i];pos[i] = i / t + 1;}for (int i = 1; i <= m; i ++)cin >> q[i].l >> q[i].r;sort (q + 1, q + 1 + m, [](Query x, Query y) {return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l];});int l = 1, r = 0; // 始终维护[l,r]的答案，对于每一次询问都移动l,r指针，使其符合询问的区间 for (int i = 1; i <= m; i ++) {while (q[i].l < l) add (-- l); while (q[i].r > r) add (++ r);while (q[i].l > l) sub (l ++);while (q[i].r < r) sub (r --);// 记录答案 ....ans[q[i].k] = res;}for (int i = 1; i <= m; i ++)cout << ans[i] << " "; return 0;
}

莫队算法主要考虑两个函数的实现add() sub()

例题：小B的询问

（https://www.luogu.com.cn/problem/P2709）

题目描述

小B 有一个长为 $n$ 的整数序列 $a$ ，值域为 $[1, k]$ 。
他一共有 $m$ 个询问，每个询问给定一个区间 $[l, r]$ ，求：

$\sum\limits_{i=1}^k c_i^2$

其中 $c_i$ 表示数字 $i$ 在 $[l, r]$ 中的出现次数。
小B请你帮助他回答询问。

输入格式

第一行三个整数 $n, m, k$ 。

第二行 $n$ 个整数，表示小B 的序列。

接下来的 $m$ 行，每行两个整数 $l, r$ 。

输出格式

输出 $m$ 行，每行一个整数，对应一个询问的答案。

输入输出样例

输入

6 4 3
1 3 2 1 1 3
1 4
2 6
3 5
5 6

输出

说明/提示

【数据范围】
对于 $100$ 的数据， $1\le n,m,k \le 5\times 10^4$ 。

思路：主要考虑add函数以及sub函数，可以定义cnt数组表示当前维护的区域 $[l, r]$ 的数字出现次数的平方和，每次新加入或者减少一个数字，计算贡献即可。

参考程序

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;template <class T> 
void read (T &x) {x = 0; char c = getchar ();while (c < '0' || c > '9') {c = getchar ();}while (c >= '0' and c <= '9') {x = (x << 3) + (x << 1) + c - 48; c = getchar ();}
}
typedef long long ll;
const int N = 5e4 + 15;
ll a[N], ans[N], pos[N], cnt[N];struct Node {int l, r, k;
}q[N];int n, m, k;
ll res;void add (int x) {cnt[a[x]] ++;res += cnt[a[x]] * cnt[a[x]] - (cnt[a[x]] - 1) * (cnt[a[x]] - 1);
}void sub (int x) {cnt[a[x]] --;res += cnt[a[x]] * cnt[a[x]] - (cnt[a[x]] + 1) * (cnt[a[x]] + 1);
}int main () {read (n), read (m), read (k);int t = sqrt (n);for (int i = 1; i <= n; i ++) {read (a[i]);pos[i] = i / t + 1;}for (int i = 1; i <= m; i ++) {read (q[i].l), read (q[i].r);q[i].k = i;}sort (q + 1, q + 1 + m, [](Node x, Node y) {return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l];	});int l = 1, r = 0;for (int i = 1; i <= m; i ++) {while (l < q[i].l) sub (l ++);while (l > q[i].l) add (-- l);while (r < q[i].r) add (++ r);while (r > q[i].r) sub (r --);ans[q[i].k] = res;}for (int i = 1; i <= m ; i ++)cout << ans[i] << endl;return 0;
}

例题：小Z的袜子

题目描述

作为一个生活散漫的人，小 $Z$ 每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小 $Z$ 再也无法忍受这恼人的找袜子过程，于是他决定听天由命……

具体来说，小 Z 把这 $N$ 只袜子从 $1$ 到 $N$ 编号，然后从编号 $L$ 到 $R$ ( $L$ 尽管小 $Z$ 并不在意两只袜子是不是完整的一双，甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。

你的任务便是告诉小 $Z$ ，他有多大的概率抽到两只颜色相同的袜子。当然，小 $Z$ 希望这个概率尽量高，所以他可能会询问多个 $(L, R)$ 以方便自己选择。

然而数据中有 L=R 的情况，请特判这种情况，输出0/1。

输入格式

输入文件第一行包含两个正整数 $N$ 和 $M$ 。 $N$ 为袜子的数量， $M$ 为小 $Z$ 所提的询问的数量。接下来一行包含 $N$ 个正整数 $C_i$ ，其中 $C_i$ 表示第 $i$ 只袜子的颜色，相同的颜色用相同的数字表示。再接下来 $M$ 行，每行两个正整数 $L, R$ 表示一个询问。

输出格式

包含 $M$ 行，对于每个询问在一行中输出分数 $A / B$ 表示从该询问的区间 $[L, R]$ 中随机抽出两只袜子颜色相同的概率。若该概率为 $0$ 则输出 0/1，否则输出的 $A / B$ 必须为最简分数。（详见样例）

输入样例

6 4
1 2 3 3 3 2
2 6
1 3
3 5
1 6

输出样例

2/5
0/1
1/1
4/15

说明/提示

$30\%$ 的数据中， $N,M\leq 5000$

$60\%$ 的数据中， $\leq 25000$

$100\%$ 的数据中， $\leq 50000$ ， $\leq L < R \leq N$ ， $C_i \leq N$ 。

思路：

使用num数组用于记录当前维护区间[l,r]中每个数字出现的次数，每次挑选两个，相同的概率为：

$\sum_{x} C_{num[x]}^{2} \,\,/\,\,C_{r-l+1}^{2}$ ，其中 $n u m [x]$ 表示颜色为 $x$ 的袜子数量。

例如：序列为2 3 3 3 2，随机抽两次，抽到相同的概率为
$(C_{2}^{2} + C_{3}^{2}) / (C_{5}^{2}) = (1+3)/10=\frac{2}{5}$

有了上述计算方法，只需要每次将add或者sub操作带来的贡献变化计算清楚即可。

参考程序

#include <iostream>
#include <algorithm>
#include <cmath>using namespace std;
typedef long long ll;
const int N = 5e4 + 15; ll a[N], pos[N], num[N], ans[N], len[N], L[N], R[N];
ll res;struct Node {int l, r, k;
}q[N];ll gcd (ll x, ll y) {return y ? gcd (y, x % y) : x;
}ll cal (ll x) {return x * (x - 1) / 2;
}void add (int x) {int t = cal(num[a[x]]);num[a[x]] ++;res += cal(num[a[x]]) - t;
}void sub (int x) {int t = cal(num[a[x]]);num[a[x]] --;res += cal(num[a[x]]) - t;
}int n, m;int main () {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m;int t = sqrt (n);for (int i = 1; i <= n; i ++) {cin >> a[i];pos[i] = i / t + 1;}for (int i = 1; i <= m; i ++) {cin >> q[i].l >> q[i].r;q[i].k = i;}sort (q + 1, q + 1 + m, [](Node x, Node y) {return pos[x.l] == pos[y.l] ? x.r < y.r : pos[x.l] < pos[y.l];	});int l = 1, r = 0;for (int i = 1; i <= m; i ++) {while (r < q[i].r) add (++ r);while (l > q[i].l) add (-- l);while (r > q[i].r) sub (r --);while (l < q[i].l) sub (l ++);ans[q[i].k] = res;len[q[i].k] = r - l + 1;}for (int i = 1; i <= m; i ++) {ll x = ans[i], y = cal(len[i]);ll d = gcd (x, y);	if (!x) cout << "0/1\n";else cout << x / d << "/" << y / d << endl;}return 0;
}

奇偶化排序

对于一些这组数据，进行分块

按照上述方法进行模拟，可以发现 $r$ 指针需要移动大概 $3000$ 次，但是实际上，如果处理完了2 1000这个区间的询问，我们直接去处理4 1000，只需要将 $l$ 移动 $2$ 次即可。如何来进行优化呢？可以使用奇偶化排序来进行，具体方法就是，对于每一块的奇偶性判断，对于奇数块的询问， $r$ 从小到大进行排序，对于偶数块的询问， $r$ 从大到小进行排序。

sort (q + 1, q + 1 + m, [](Node x, Node y) {if (pos[x.l] == pos[y.l]) if (pos[x.l] & 1) return x.r < y.r; // 奇数块else return x.r > y.r;  // 偶数块else return pos[x.l] < pos[y.l];	 });

带修改的莫队

普通的莫队算法，是不支持修改的。如果在查询过程修，加上一个修改操作，该如何处理这样的问题呢？

数颜色 / 维护队列 （https://www.luogu.com.cn/problem/P1903）

题目描述

墨墨购买了一套 $N$ 支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

$Q\ L\ R$ 代表询问你从第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。
$R\ P\ Col$ 把第 $P$ 支画笔替换为颜色 $C o l$ 。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入格式

第 $1$ 行两个整数 $N$ ， $M$ ，分别代表初始画笔的数量以及墨墨会做的事情的个数。

第 $2$ 行 $N$ 个整数，分别代表初始画笔排中第 $i$ 支画笔的颜色。

第 $3$ 行到第 $2 + M$ 行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式

对于每一个 Query 的询问，你需要在对应的行中给出一个数字，代表第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。

对于支持单点修改的操作，如果仍要使用莫队算法，我们需要在询问中加上一个表示次数的变量，用于记录该次询问之前经历过几次修改。

我们仍然按照普通莫队的思路进行考虑，即：始终维护区间 $[l, r]$ ，通过每次移动一个点，扩散 $[l, r]$ 的范围，直到符合我们的询问范围为止，我们仍然可以先进行扩散，当满足某个询问时，我们可以查询在这个询问之前经历过多少次的修改，对于每一次修改，如果是在当前询问的范围内，我们需要先减去原先未修改的贡献，然后更新该点，再把新的贡献加进去，可以通过 $c h a n g e$ 函数实现。

struct Node {int l, r, k, cnt;  //q[i].cnt表示到I的时候共有几次修改操作
}q[N];struct Node1 {int x, y;
}c[N];  // 记录单点修改操作, x表示要修改的点的位置，y表示要将第x个点改为y/**需要特别留意的是第二个语句，没有直接赋值，而是用了swap因为我们在处理之后的询问，有可能需要还原这个修改操作，所以我们需要时刻记录修改的值，不能直接无脑的覆盖
**/ 
void change (int l, int r, int num) {if (c[num].x >= l and c[num].x <= r) sub (c[num].x); // 减去要修改的点所带来的贡献，因为我们在移动l,r是，默认是都没有修改的。swap (a[c[num].x], c[num].y); if (c[num].x >= l and c[num].x <= r) add (c[num].x); // 更新之后得点需要加上它的贡献。
}

实际上，我们加上了修改次数，对于这些修改，也是类似的方法一次一次的去更新修改，因此整体操作也可以离线进行，排序的方式，首先安装左端点是否在一个块内排序，然后是右端点，最后是修改次数。

玄学：洛谷上这道题，分块大小为 $n^{\frac{2}{3}}$ ,否则会TLE。

参考程序

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;const int N = 1e6 + 15;int a[N], pos[N], ans[N], num[N];struct Node {int l, r, k, cnt;  //q[i].cnt表示到I的时候共有几次修改操作
}q[N];struct Node1 {int x, y;
}c[N];  // 记录单点修改操作, x表示要修改的点的位置，y表示要将第x个点改为yint n, m, res;void add (int x) {num[a[x]] ++;if (num[a[x]] == 1) res ++;
}void sub (int x) {num[a[x]] --;if (!num[a[x]]) res --;
}void change (int l, int r, int num) {if (c[num].x >= l and c[num].x <= r) sub (c[num].x); // 减去要修改的点所带来的贡献，因为我们在移动l,r是，默认是都没有修改的。swap (a[c[num].x], c[num].y); if (c[num].x >= l and c[num].x <= r) add (c[num].x); // 更新之后得点需要加上它的贡献。
}int main () {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m;int t = pow (n, 2.0 / 3);for (int i = 1; i <= n; i ++) {cin >> a[i];pos[i] = i / t + 1;}int ql = 0, cl = 0;for (int i = 1; i <= m; i ++) {char s[3];cin >> s;if (*s == 'Q') {++ ql;cin >> q[ql].l >> q[ql].r;q[ql].k = ql;q[ql].cnt = cl;} else {++ cl;cin >> c[cl].x >> c[cl].y;}}sort (q + 1, q + 1 + ql, [] (Node x, Node y) {if (pos[x.l] != pos[y.l]) return pos[x.l] < pos[y.l];else if (pos[x.r] != pos[y.r]) return pos[x.r] < pos[y.r];else return x.cnt < y.cnt;});int l = 1, r = 0, num = 0;for (int i = 1; i <= ql; i ++) {while (l < q[i].l) sub (l ++);while (l > q[i].l) add (-- l);while (r < q[i].r) add (++ r);while (r > q[i].r) sub (r --);while (num < q[i].cnt) change (l, r, ++ num);while (num > q[i].cnt) change (l, r, num --);ans[q[i].k] = res;}for (int i = 1; i <= ql; i ++) cout << ans[i] << endl;return 0;
}