Python代码

import numpy as np
from scipy.stats import chi2_contingencyd = np.array([[2, 1, 1, 0, 276], [9, 7, 4, 2, 258]])
print(chi2_contingency(d))
# 第一个值为卡方值，
# 第二个值为P值，
# 第三个值为自由度，
# 第四个为与原数据数组同维度的对应期望值

结果显示

卡方值：13.361287027579163
P值：0.009638978128151272
自由度：4
与原数据数组同维度的对应期望值：array([
[  5.5,   4. ,   2.5,   1. , 267. ],
[  5.5,   4. ,   2.5,   1. , 267. ]
])

用Excel表格也能做

先给出原始数据，再算期望值，最后算卡方值
原始数据为

卡方值计算公式为
$$X^2=卡方值=\frac{(抽样数据-期望值{)}^2}{期望值}$$
$$X^2的值越大，说明“观测组与对照组有关系”成立的可能性越大。$$
P值由下面函数实现

=CHIDIST(卡方值,自由度)

结果图如下

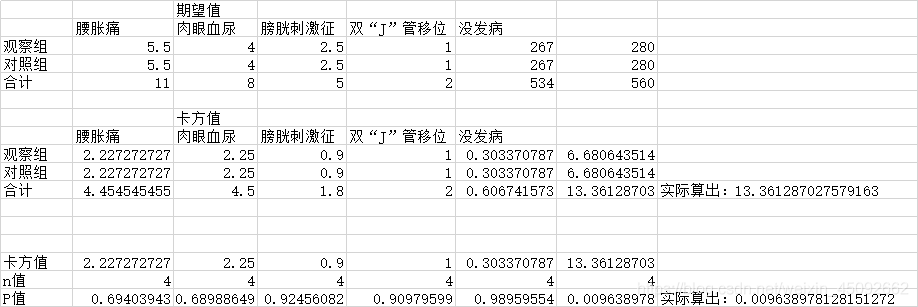
当P = 0.05，n = 4时，卡方值 = 9.487729037
此时的卡方值为 13.361287027579163 > 9.487729037
故观察组与对照组有关系。

有用请点个赞！！
本站所有文章均为原创，欢迎转载，请注明文章出处：https://blog.csdn.net/weixin_45092662。百度和各类采集站皆不可信，搜索请谨慎鉴别。技术类文章一般都有时效性，本人习惯不定期对自己的博文进行修正和更新，因此请访问出处以查看本文的最新版本。