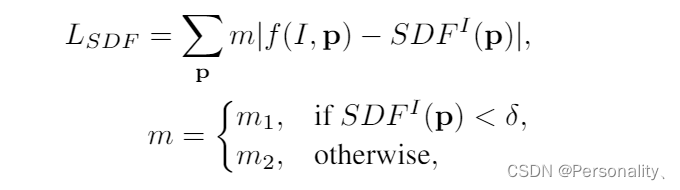上一篇博客中讲述了使用$Random$算法进行$quantile$估算，详情可见Random，本博客将讲诉另外一个$quantile$估算算法：$T-digest$，该算法理论基础可以参考Computing Extremely Accurate Quantiles Using t-Digest

算法

算法原理

该算法的思想是将输入数据表示缩减成簇的集合 { C i } 1 m \{C_{i}\}^m_1 {Ci​}1m​，每个簇表示为：$(C_i,C_{count})$，$C_i$表示该簇的中心，一般是等于簇中元素的平均值，$C_{count}$则是该簇中对应的元素的数量。簇的大小极大影响了算法的准确率，假设簇的较大，则会导致结果误差偏大；假设簇的大小较小，则会导致结果准确，但另一方面计算的复杂度对增加。对于一般的问题而言，我们更加关注位于两端的$quantile$（即靠近$0$或者$1$），即：$quantile$位于中间部分的簇容量较大；相应地，$quantile$位于两端的簇的容量较小。给出如下公式：
$$k(q,\sigma )=\frac{\sigma }{2\pi }arcsin(2q-1)\text{\hspace{1em}(1)}$$
其中：$q$为簇对应的分位数，$\sigma$为压缩系数。
则对应的某段$quantile$所能代表的量化长度为：
$$K(C_i)=k(q(c_i),\sigma )-k(q(c_{i-1}),\sigma )\text{\hspace{1em}(2)}$$
其中：$K(C_1)=k(q(c_1),\sigma )$
另外，$T-digest$还需满足以下性质：
$$\{\begin{array}{rlr}K(c_i)& =& \le 1\\ K(c_i)+K(c_{i+1})& >& 1\end{array}\text{\hspace{1em}(3)}$$
对于某个簇$C_i$而言，其所能接受的最大$quantile$为：
$$q_{limit}=\frac{1}{2}[1+sin(arcsin(2\times q(c_i)-1)+\frac{2\pi }{\sigma })]$$
故当某个新元素到来时，若将其加入到当前簇$C_i$时，若$q$将大于$q_{limit}$，则不将其加入；否则，则将其加入。下图给出了其算法示意图：

空间消耗及错误界限

压缩系数$\sigma$，$buffer$大小$k$，簇的数量$\lfloor \frac{\sigma }{2}\rfloor \le m\le \lceil \sigma \rceil$

不像其他$quantile$估算算法，该算法的准确率$ϵ$正比于$q\times (1-q)$，其中$q$就是分位数。

示例

T-digest的建立

T-digest的查询

相关链接

TDigest 算法原理
TDigest_PPT