整理并翻译自吴恩达深度学习视频，卷及神经网络第四章4.1-4.5，有所详略。

人脸验证和人脸识别

Verification与Recognition的差异：

验证：

• 输入图像，名字/ID
• 输出输入的图像是否和输入的名字/ID是同一个人

这是个1:1问题。

识别：

• 你有一个K个人的数据库
• 获取一张图像作为输入
• 如果它属于K个人之一，输出这张图像对应的ID(不属于任何一个，输出不能识别)

这是个1:100问题，需要更高的准确度保证不会出错以满足我们对准确性的要求(Maybe need more than 99.9 % accuracy)。

One-Shot学习

One shot, one kill - war3暗夜精灵族弓箭手语音。

意思很直观，你需要在仅有一个example作为输入的情况下给出正确的结果。

如果按之前我们对网络的训练方式，我们不能训练出一个足够健壮的网络因为输入实在是太少了。

而且每次如果有新人加入的团队，你不能总得重新训练你的网络，这显然不是一个好的方法。

相似度 函数

因此我们将学习的目标更改为学习两张图片之间的的差异程度。
$Ifd(img1,img2)\le \tau$ “same”
$Ifd(img1,img2)>\tau$ “different”

小于等于某个阀值，判定是同一个人；否则判定不是同一个人。

我个人觉得叫差异度函数更合适。这篇博文后面就使用差异度函数了。

Siamese network

The job of function d which you learned about last video is to input two faces and tell you how similar or how different they are, a good way to this is to use aSiamese Network

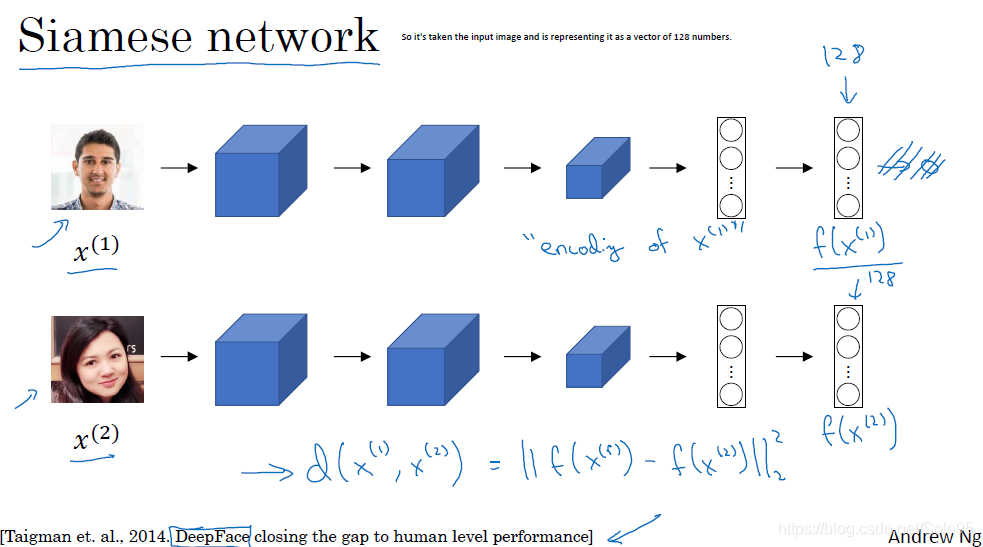
去掉普通卷积网络全连接层之后的输出层，我们把输入经过卷积网络之后得到的128维的vector作为输入x的编码。我们就得到了一个Siamese网络。

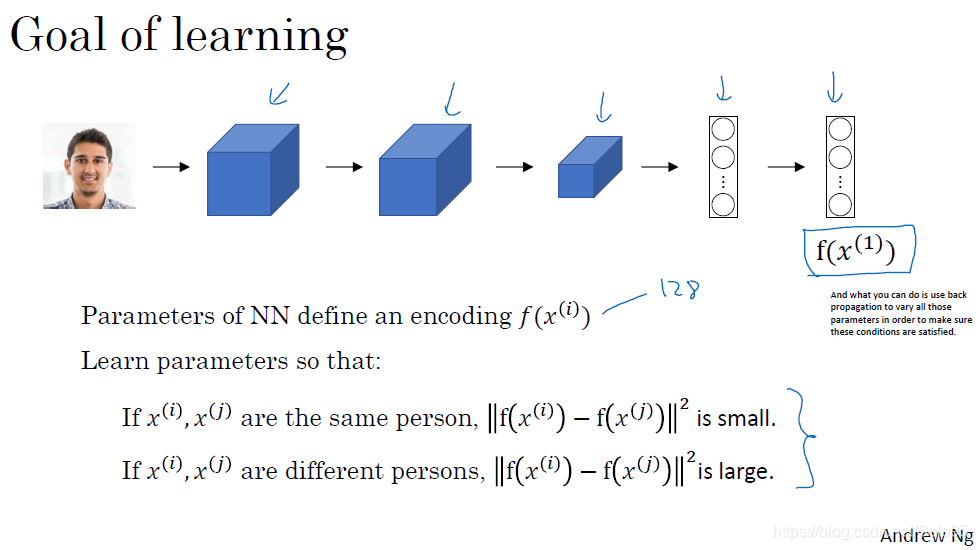
把两张图像经过网络得到的vector记为f(x¹)和f(x²)，定义差异度函数为
$$||f(x^{(i)}-f(x^{(j)})|{|}^2$$
如果是同一个人，那么该函数应当很小；如果不是同一个人，那么该函数应该很大。我们学习的目标就是学习到一组parameter，这组parameter能够使得该函数实现同一个人时其值很小，不是同一个人时其值很大的。

三元组损失(TripletLoss)

One way to learn the parameters of the neural network so that it gives you a good encoding for your pictures of faces is to define and apply gradient descent on the
triplet loss function

更科学的方法：我们定义学习目标为三元组(A, P, N)之间的组合公式(过程如上图)：
$$||f(A)-f(P)|{|}^2-||f(A)-f(N)|{|}^2+\alpha \le 0$$

其中，A代表Anchor即输入的一个图像，P代表Positive，即正例，N代表Negative，即反例。$\alpha$即为SVM里面的margin。

对上述公式和0之间取max，作为我们的损失函数：
$$l(A,P,N)=max(||f(A)-f(P)|{|}^2-||f(A)-f(N)|{|}^2+\alpha ,0)$$
损失函数衡量的是不对的情况，因此它是训练目标取反。上式的意义的在于$\alpha$是个大于0的定值，因此$||f(A)-f(P)|{|}^2-||f(A)-f(N)|{|}^2$取较大的值时，表示我们的损失也很大。

整个训练集上的损失函数即为：
$$J=\sum _1^{m}l(A^{(i)},P^{(i)},N^{(i)})$$

在训练数据三元组的选取上，我们选"难"训练的三元组收益更大，"难"直观上的理解是，$d(A,P)+\alpha$很大，$d(A,N)$很小，这样使得算法必须竭尽全力地学习到使$d(A,P)+\alpha$变小，同时使$d(A,N)$变大的parameter，这提高了算法的计算效率。

人脸识别与二元分类

将人脸识别看作二元分类是三元组损失的另外一种替代方案。

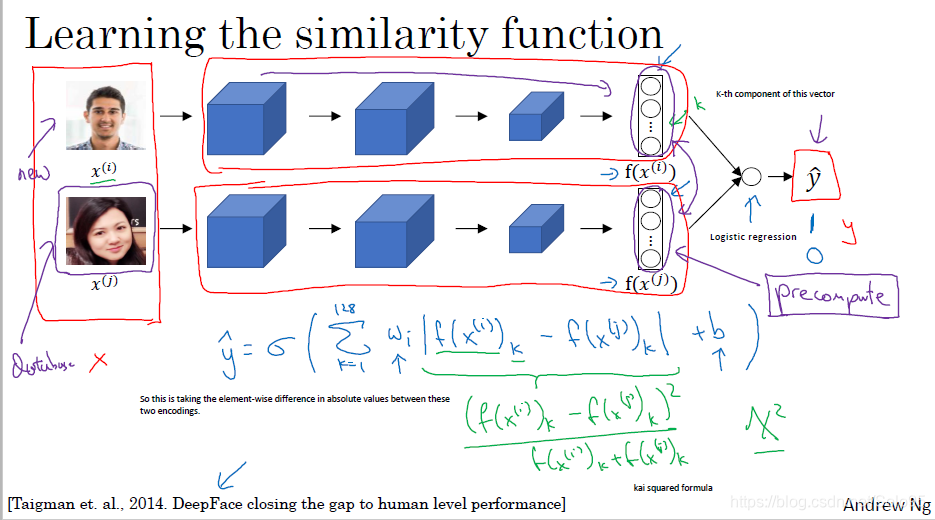
我们使用2个Siamese网络得到2张输入图像的2个vector，取这2个vector作为logistic regression的输入，如果2张图像输入同一个人，那么logistics regression应该输出1(或者大于某个阀值)，否则输出0。基于此收集训练数据(或者小于某个阀值)。

假设logistic regerssion使用$\sigma$函数，那么输出
$$y=\sigma (\sum _{k=1}^{128}{w}_i|f(x_k^{(i)})-x_k^{(j)})|+b)$$

如同普通的逻辑回归一样，你训练网络，得到$w_i$和$b$，然后使用这些参数去判断给定的2张图片是否是同一个人。

一个实际部署的小trick是，你可以预先计算数据库出里员工的图像的vector然后存储起来，这样可以节省大量的计算资源，加快你整个系统的响应速度。

将人脸识别看作二元分类监督问题，你使用一组图像当做输入，输出1或者0如上图所示。