note

• 对某一节点的标签进行预测，需要其本身特征、邻居的标签和特征。message passing的假设是图中相似的节点之间会存在链接，也就是相邻节点有标签相同的倾向。这种现象可以用homophily（相似节点倾向于聚集）、influence（关系会影响节点行为）、confounding（环境影响行为和关系）来解释。
• collective classification给所有节点同时预测标签的概率分布，基于马尔科夫假设（某一点标签仅取决于其邻居的标签）。
  local classifier（用节点特征预测标签）→ relational classifier（用邻居标签 和/或 特征，预测节点标签）→ collective inference（持续迭代）。有三种collective classification技术：
  • relational classification：用邻居标签概率的加权平均值来代表节点标签概率，循环迭代求解
  • iterative classification：在训练集上训练用 (节点特征) 和 (节点特征, 邻居标签summary $\mathrm{z}$ ) 两种 自变量预测标签的分类器 ${\varphi }_1$ 和 ${\varphi }_2$, 在测试集上用 ${\varphi }_1$ 赋予初始标签, 循环迭代求解 $\mathrm{z}\rightleftharpoons$ 用 ${\varphi }_2$ 重新预测标签
  • belief propagation：在边上传递节点对邻居的标签概率的置信度（belief）的message/estimate，迭代计算边上的message，最终得到节点的belief。有环时可能出现问题。
• relational classifiers没有使用节点特征信息，iterative classification有。
• Correct & Smooth利用浅层模型MLP，误差纠正和预测平滑实现节点分类效果超越一般GNN模型。但是是直推式学习，也仅考虑了节点分类。

一、半监督节点分类：标签传播和消息传递

本task内容：

• 半监督节点分类问题的常见解决方法：特征工程、图嵌入表示学习、标签传播、图神经网络。
• 基于“物以类聚，人以群分”的Homophily假设，进行Label Propagation、Relational Classification（标签传播）、Iterative Classification、Correct & Smooth（C & S）、Loopy Belief Propagation（消息传递）、Masked Lable Prediction等半监督和自监督节点分类方法。
• 这些方法经常被用于节点分类任务的Baseline比较基线。消息传递和聚合的思路也影响了后续图神经网络的设计。

1.1 线性代数知识补充

当且仅当矩阵谱半径严格小于1，矩阵乘幂收敛。

谱半径指最大奇异值的模长。

对称矩阵、非对称矩阵中的可对角化矩阵：最大奇异值就是最大特征值的平方，奇异值和特征值一一对应。
非对称矩阵，不可对角化矩阵：不便讨论

1.2 半监督节点分类问题-求解方法对比

方法	图嵌入	表示学习	使用属性特征	使用标注	直推式	归纳式
人工特征工程	是	否	否	否	/	/
基于随机游走的方法	是	是	否	否	是	否
基于矩阵分解的方法	是	是	否	否	是	否
标签传播	否	否	是/否	是	是	否
图神经网络	是	是	是	是	是	是

• 人工特征工程：节点重要度、集群系数、Graphlet等。

• 基于随机游走的方法，构造自监督表示学习任务实现图嵌入。无法泛化到新节点。

  例如：DeepWalk、Node2Vec、LINE、SDNE等。

• 标签传播：假设“物以类聚，人以群分”，利用邻域节点类别猜测当前节点类别。无法泛化到新节点。

  例如：Label Propagation、Iterative Classification、Belief Propagation、Correct & Smooth等。

• 图神经网络：利用深度学习和神经网络，构造邻域节点信息聚合计算图，实现节点嵌入和类别预测。

  可泛化到新节点。

  例如：GCN、GraphSAGE、GAT、GIN等。

1.3 Message Passing and Node Classification

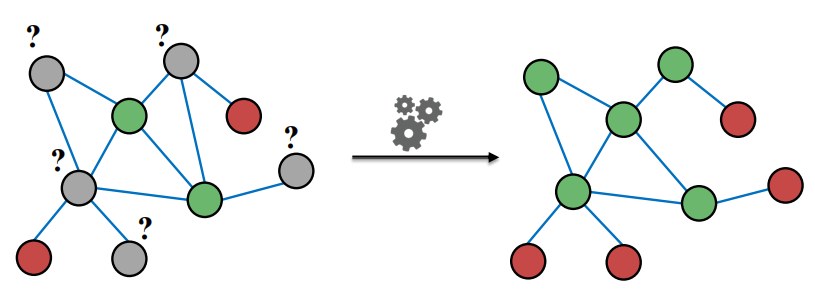
• 半监督学习，使用node embedding，基于”网络中存在关系correlations“，相似节点之间存在连接。利用collective classification同时将标签分配到网络中的所有节点上。
• correlation的两种原因：
  • homophily（物以类聚人以群分）：个体特征影响社交连接
  • influence：社交连接影响个体特征，如用户将喜欢的音乐推荐给朋友
• 预测节点 v 的标签需要：v 的特征；v 邻居的标签；v 邻居的特征
• example task：
  
• 解决方法：collective classification。collective classification的应用：
  • Document classification
  • 词性标注Part of speech tagging
  • Link prediction
  • 光学字符识别Optical character recognition
  • Image/3D data segmentation
  • 实体解析Entity resolution in sensor networks
  • 垃圾邮件Spam and fraud detection
• collective classification：使用probabilistic framework
  • Markov Assumption: the label $Y_v$ of one node $v$ depends on the labels of its neighbors $N_v$
    $$P\left(Y_v\right)=P\left(Y_v\mid N_v\right)$$

二、四种半监督学习进行节点分类

2.1 Relational Classification / Probabilistic Relational Classifier

• 基本思想：节点v的类别概率是邻居节点的加权平均值。对于无标签节点，初始化类别概率${\mathrm{Y}}_{\mathrm{v}}$为0.5。以随机顺序更新所有无标签节点，直至收敛到最大迭代次数。
• 更新公式（如果是异质图， 则$A_{v,u}$可以是v到u节点之间的边权重；$P\left(Y_v=c\right)$为节点v标签为c的概率值）：$$P\left(Y_v=c\right)=\frac{1}{{\sum }_{(v,u)\in E}{A}_{v,u}}\sum _{(v,u)\in E}{A}_{v,u}P\left(Y_u=c\right)$$
• 两个缺点：
  • 节点的概率值更新不一定能收敛
  • 模型无法使用节点特征信息
    

2.2 Iterative Classification

（1）basic idea

• 基本思想：基于节点特征和邻居节点label，对节点进行分类
• 训练2个分类器：
  • base classifier：${\varphi }_1\left(f_v\right)$，基于当前节点v特征进行预测节点label
  • relational classifier： ${\varphi }_2\left(f_v,z_v\right)$，基于当前节点v特征和周围节点信息$z_v$进行预测节点label
• 计算$z_v$：可以是邻居label的比例、邻居出现最多的label、邻居label的类别数等。

（2）iterativate classifier architecture

（3）ex：web page classification

• step1：在训练集上训练 ${\varphi }_1$ 和 ${\varphi }_2$
• step2：在测试集上预测标签
  • 用 ${\varphi }_1$ 预测 $Y_{\mathrm{v}}$
  • 循环迭代：
    • 用 $Y_{\mathrm{v}}$ 计算 $z_{\mathrm{v}}$
    • 用 ${\varphi }_2$ 预测标签
    • 迭代到收敛为止

2.3 Correct & Smooth

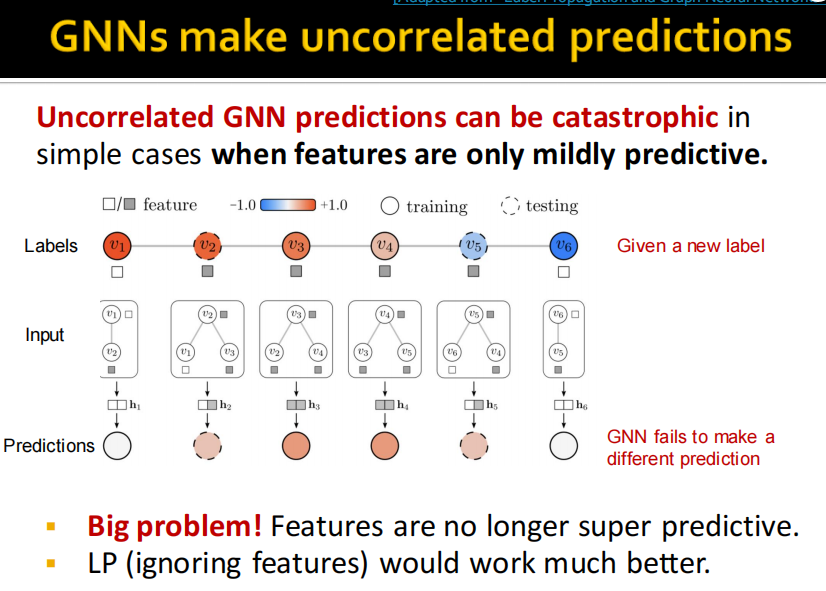
（1）motivation： LP和GNN

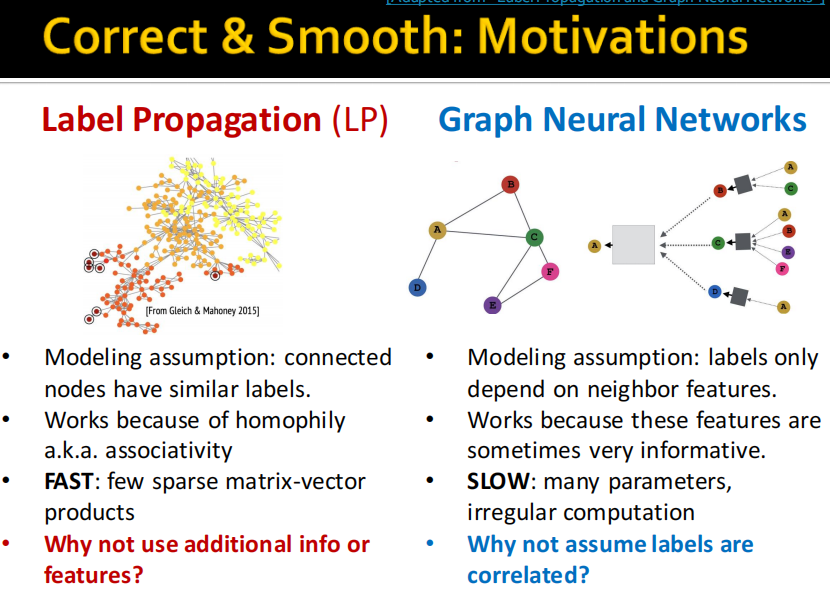
label propagation是基于homophily和associativity进行的，如果比较少的
2023年一月在OGB leaderboard上C&S算法达到SOTA.

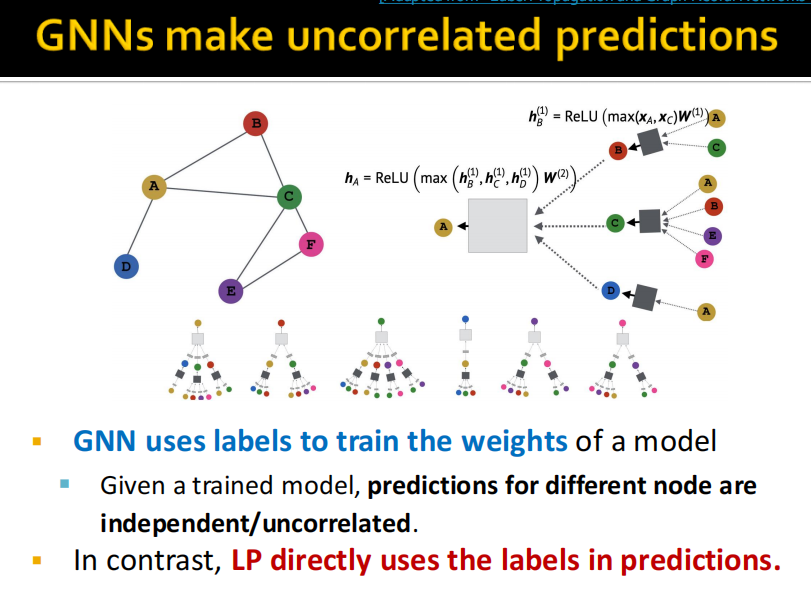
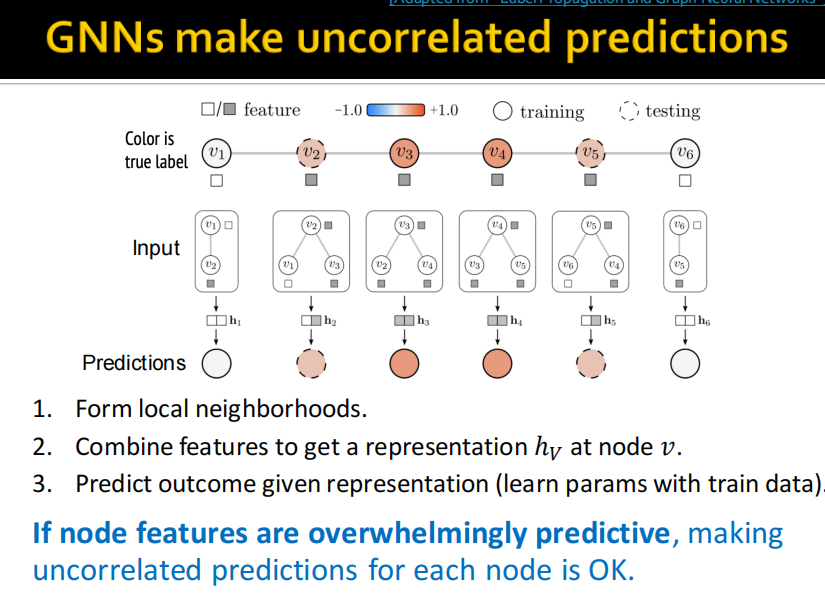
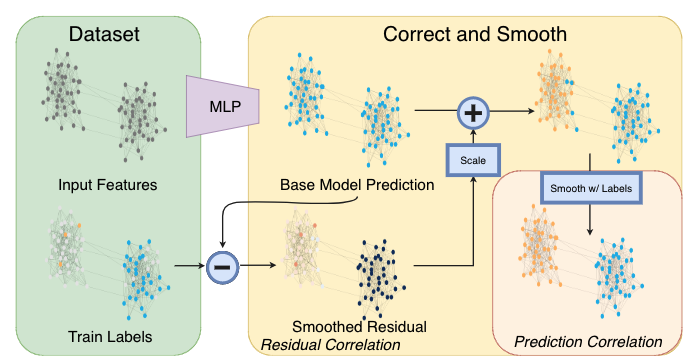
（2）C&S model architecture

• 「基础预测模型」：仅依赖节点特征并且忽略图的结构，例如 MLP 或者线性模型；
• 「修正步骤」：将训练数据中的不确定性传播到整个图以此来修正基础预测结果；
• 「平滑步骤」：对节点预测结果进行平滑。

其中「修正步骤」和「平滑步骤」是基于半监督学习的标签传播思想进行改进的，整个框架没有利用图结构来学习模型参数因此参数量非常少而且不需要大量的时间来训练模型，但实验效果却非常好。

• correct step（修正步骤）

  • step1：计算每个节点的训练误差（ground-truth label减去soft label）
  • step2：
    • Diffuse training errors ${\mathbf{E}}^{(0)}$ along the edges
    • 将邻接矩阵A转为diffusion矩阵（归一化后）
  • step3：迭代计算：${\mathbf{E}}^{(t+1)}\leftarrow (1-\alpha )\cdot {\mathbf{E}}^{(t)}+\alpha \cdot \tilde{\mathbf{A}}{\mathbf{E}}^{(t)}$，其中$\alpha$是超参数
  • step4：将归一化的diffused training errors加到预测值soft labels

• smooth step（平滑步骤）
  

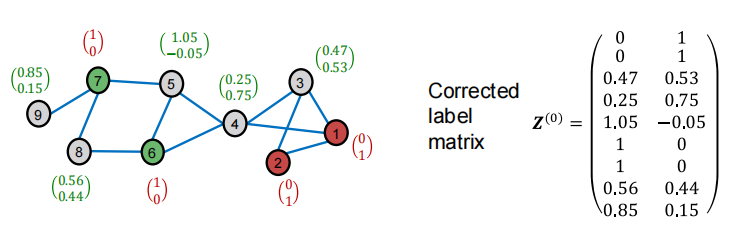
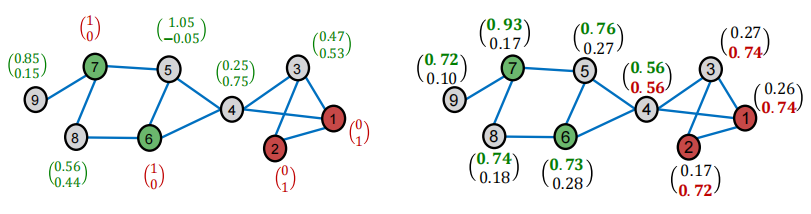
  • step1：根据图结构Diffuse label ${\mathbf{Z}}^{(0)}$
  • step2：$Z^{(t+1)}\leftarrow (1-\alpha )\cdot Z^{(t)}+\alpha \cdot \tilde{A}{Z}^{(t)}$，其中$\alpha$是超参数

smooth的两个步骤对应下图：

（3）diffusion matrix $\tilde{A}$

• 给邻接矩阵A添加self-loop，归一化操作：$\tilde{\mathbf{A}}\equiv {\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}$
• $\mathbf{D}\equiv \mathrm{Diag}\left(d_1,\dots ,d_N\right)$为度矩阵
• 如果i节点和j节点相连，则边的权重${\tilde{A}}_{ij}$ 为$\frac{1}{\sqrt{d_i\sqrt{d_j}}}$。
  • 如果i和j节点相连，且该两个节点分别没有连接其他节点，则${\tilde{A}}_{ij}$较大
  • 如果i和j节点相连，且该两个节点分别有连接其他节点，则${\tilde{A}}_{ij}$较小
• All the eigenvalues $\lambda$ 's are in the range of $[-1,1]$.
• Eigenvector for $\lambda =1$ is ${\mathbf{D}}^{1/2}1$ ( $1$ is an all-one vector).
  • Proof: $\tilde{A}{\mathbf{D}}^{1/2}1={\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2}{\mathbf{D}}^{1/2}1=$ $D^{-1/2}A1=D^{-1/2}D1=1\cdot D^{1/2}1$.
  • $\mathbf{A}1=\mathbf{D}1$, since they both leads to node degree vector
• 参考：Semi-Supervised Learning Using Gaussian Fields and Harmonic Functions.ICML 2013

（4）summary

• Correct & Smooth (C&S) uses graph structure
  to post-process the soft node labels predicted
  by any base model.
• Correction step: Diffuse and correct for the
  training errors of the base predictor.
• Smooth step: Smoothen the prediction of the
  base predictor (a variant of label propagation).
• C&S can be combined with GNNs
  • C&S achieves strong performance on semisupervised node classification

2.4 Masked label prediction

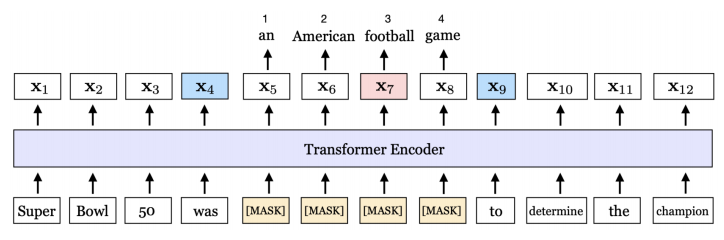
• 训练：随机将节点label设为0，然后用$[X,\tilde{Y}]$ 预测已标记的节点标签
• 推理：使用 $\tilde{Y}$ 预测末标注的节点

四、总结

4.1 小结

• Node embeddings
  • Embed nodes into Euclidean space, and use
    distance metric in embedding space to approximate
    node similarity
• Graph Neural Networks
  • Iterative neighborhood aggregation
• Label Propagation
  • Inductive bias: homophily
  • Explicitly incorporate label information when
    making predictions

4.2 思考题

哪些图数据挖掘问题，可以抽象成半监督节点分类问题？

有哪些解决半监督节点分类问题的方法？各有什么特点？（对照表格简述）

如何理解Transductive Learning（直推式学习）？

如何理解Inductive Learning（归纳式学习）？

本讲讲了哪些标签传播和集体分类方法？

如何理解网络中的Homophily？

简述Label Propagation的算法原理。

Label Propagation是否用到了节点的属性特征？

简述Iterative Classification的算法原理。

Iterative Classification如何使用节点之间的关联信息？

为什么Relational Classification和Iterative Classification都不保证收敛？

简述C & S的基本原理

如何计算Normalized Adjacency Matrix？

如何用图论解释成语“三人成虎”、“众口铄金”？

如何用图论解释《三体》中的“猜疑链”？

简述Loopy Belief Propagation的基本原理。

简述Masked Label Prediction的基本原理。

Masked Label Prediction可以是Inductive的吗？可以泛化到新来的节点吗？

本讲的方法，与图神经网络相比，有何异同和优劣？

如何重新理解“出淤泥而不染”？

如何重新理解“传销”、“病毒式裂变”？

附：时间安排

任务	任务内容	截止时间	注意事项
	2月11日开始
task1	图机器学习导论	2月14日周二	完成
task2	图的表示和特征工程	2月15、16日周四	完成
task3	NetworkX工具包实践	2月17、18日周六	完成
task4	图嵌入表示	2月19、20日周一	完成
task5	deepwalk、Node2vec论文精读	2月21、22、23、24日周五	完成
task6	PageRank	2月25、26日周日	完成
task7	标签传播与节点分类	2月27、28日周二	完成
task8	图神经网络基础	3月1、2日周四
task9	图神经网络的表示能力	3月3日周五
task10	图卷积神经网络GCN	3月4日周六
task11	图神经网络GraphSAGE	3月5日周七
task12	图神经网络GAT	3月6日周一

Reference

[1] C&S：标签传播思想与浅层模型相结合性能即可超过图神经网络
[2] CS224W官网：https://web.stanford.edu/class/cs224w/index.html
[3] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[4] cs224w（图机器学习）2021冬季课程学习笔记6 Message Passing and Node Classification
[5] https://www.bilibili.com/video/BV1184y1G7pA
[6] 扩展阅读：https://github.com/TommyZihao/zihao_course/blob/main/CS224W/5-Semi.md

中文精讲视频：https://www.bilibili.com/video/BV1184y1G7pA

Youtube视频：

https://www.youtube.com/watch?v=6g9vtxUmfwM&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=14

https://www.youtube.com/watch?v=QUO-HQ44EDc&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=15

https://www.youtube.com/watch?v=kh3I_UTtUOo&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=16
[7] D Easley, Kleinberg J . Networks, Crowds, and Markets[M]. Cambridge University Press, 2010：https://www.cs.cornell.edu/home/kleinber/networks-book/networks-book.pdf
[8] 半监督节点分类：标签传播和消息传递【斯坦福CS224W图机器学习】子豪
[9] ICLR2021 的《Combining Label Propagation and Simple Models OUT-PERFORMS Graph Networks》
[10] 标签传播与标签平滑