输出100 - 200之间的素数

素数就是质数，即除了1和它本身不再有求它因数的自然数
那么这道题的思路就是用100到200之间的数去除以比这个数小的所有数（除了1和它本身），如果有余数说明它不是一个素数
看下面代码：

int main()
{int i = 0;int count = 0;// 外层循环用来获取100~200之间的所有数据，100肯定不是素数，因此i从101开始for(i=101; i<=200; i++){//判断i是否为素数：用[2, i)之间的每个数据去被i除，只要有一个可以被整除，则不是素数int j = 0;for(j=2; j<i; j++){if(i%j == 0){break;}}// 上述循环结束之后，如果j和i相等，说明[2, i）之间的所有数据都不能被i整除，则i为素数if(j==i){count++;//记录质数的个数printf("%d ", i);}}printf("\ncount = %d\n", count);return 0;
}

当然这个代码还可以优化
因为偶数不可能是质数，所以我们让 i 每次循环 +2
超过i一半的数据，i 一定不是它的倍数
所以代码如下：

int main()
{int i = 0;//初始值设为101，每次+=2，因为偶数一定不是素数for (i = 101; i < 200; i += 2){int j = 0;//大于i/2的数一定不能被i整除  for (j = 2; j <= i / 2; j++){if (i % j == 0){break;}}// 上述循环结束之后，如果j>(i/2)，说明[2, i/2）之间的所有数据都不能被i整除，则i为素数if (j > i / 2){printf("%d ", i);}}return 0;
}

还有一个算法就是 i的因子 < sqrt(i)
这是什么意思呢？
首先 sqrt 是开平方的意思
在这里插入图片描述
所以我们只需要让因子小于 “36开平方” 就可以了
代码如下：

int main()
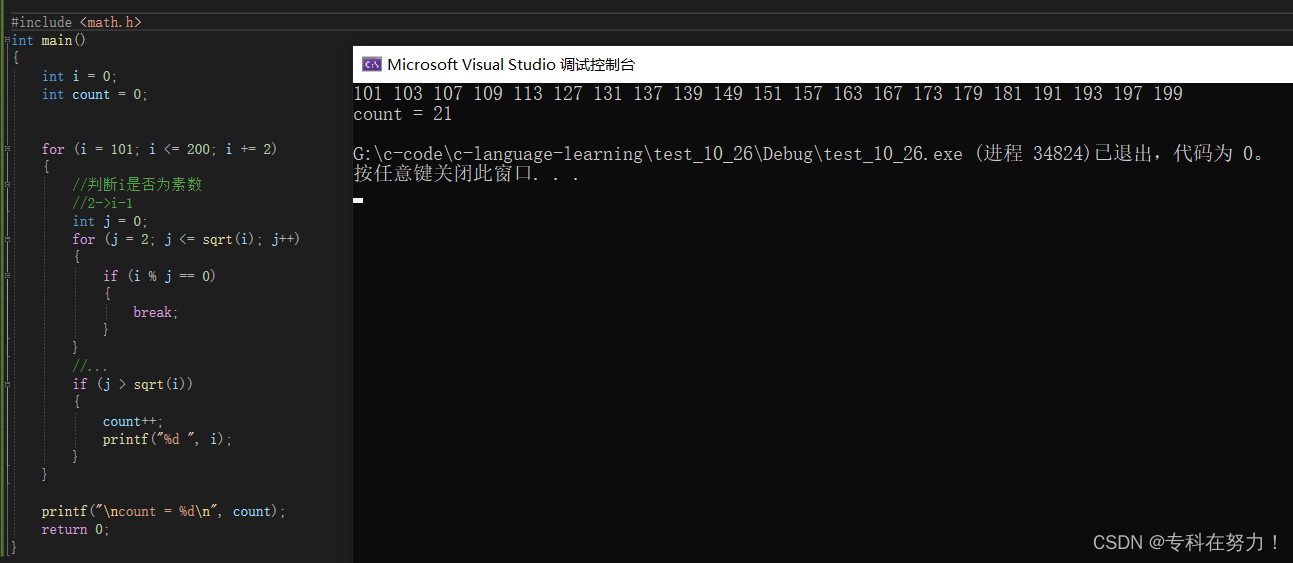
{int i = 0;int count = 0;//记录素数的个数for (i = 101; i <= 200; i += 2){//判断i是否为素数//2->i-1int j = 0;for (j = 2; j <= sqrt(i); j++){if (i % j == 0){break;}}//...if (j > sqrt(i)){count++;printf("%d ", i);}}printf("\ncount = %d\n", count);return 0;
}