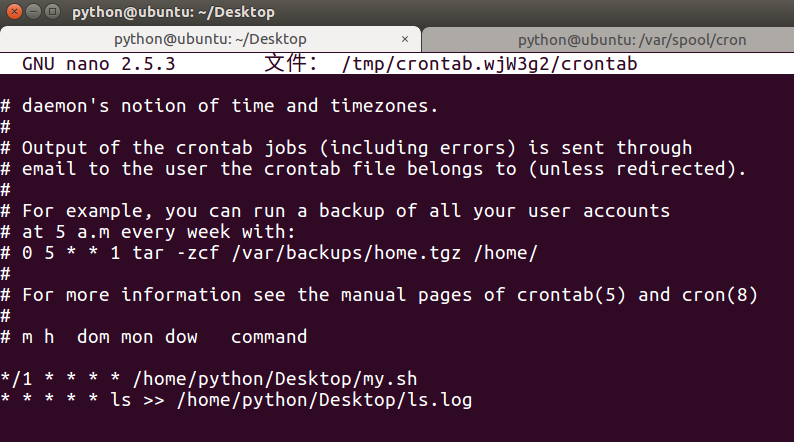
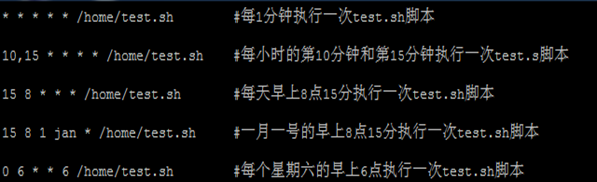
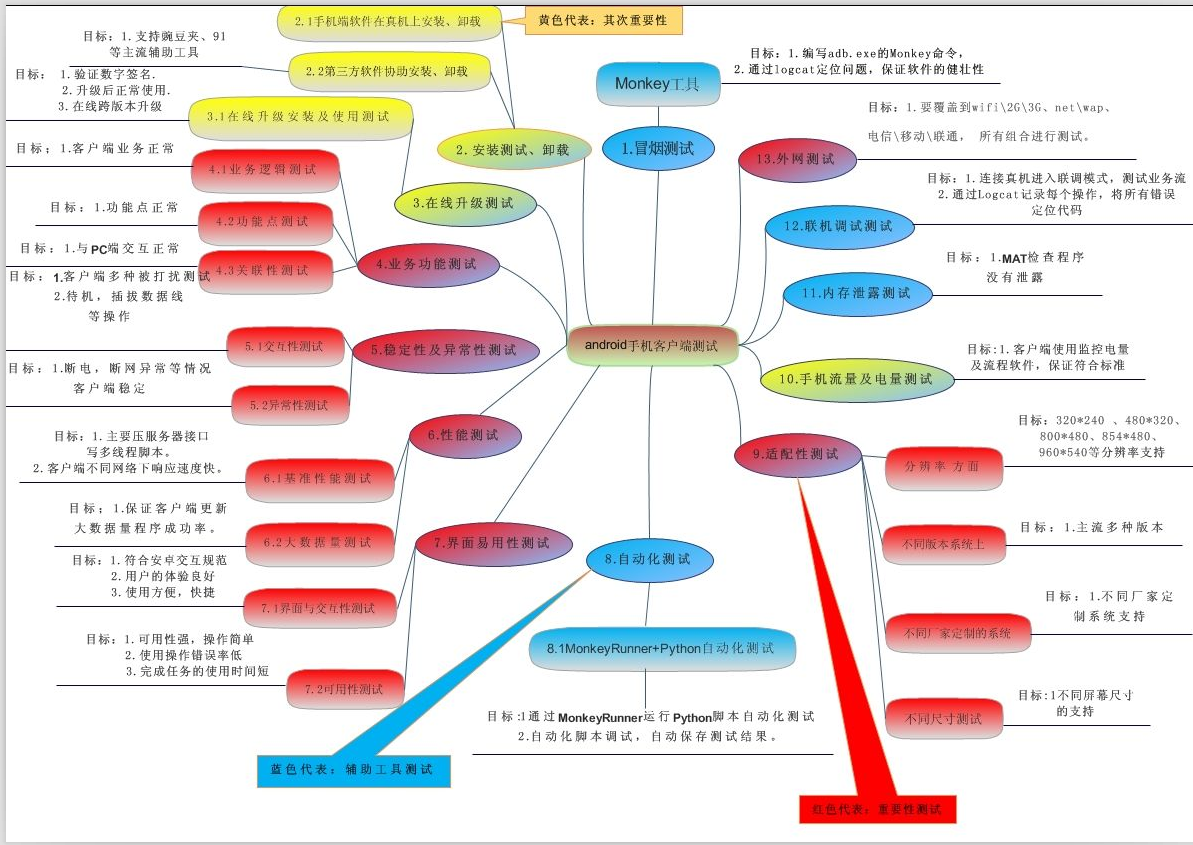
1 MAE
- Mean Absolute Error ,平均绝对误差
- 是绝对误差的平均值
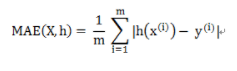
for x, y in data_iter:y=model(x)d = np.abs(y - y_pred)mae += d.tolist()#mae=sigma(|pred(x)-y|)/m
MAE = np.array(mae).mean()MAE/RMSE需要结合真实值的量纲才能判断差异。
下图是指,假如ground truth是0,那么MAE和prediction之间的关系(后同)
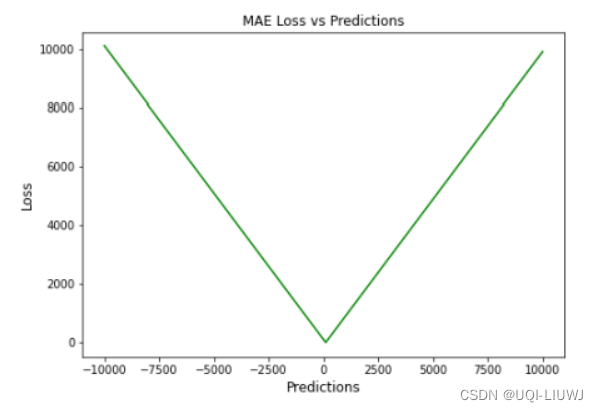
1.1 优缺点
优点:
- 计算简单
- 对异常值不太敏感
缺点:
- 在prediction已经很接近ground-truth的时候,梯度依然很大——>可能在梯度下降的时候跳过最小值
2 RMSE
- Root Mean Square Error,均方根误差
- 是观测值与真值偏差的平方和与观测次数m比值的平方根。
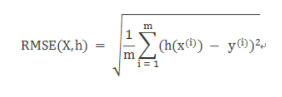
for x, y in data_iter:y=model(x)d = np.abs(y - y_pred)mse += (d ** 2).tolist()#mse=sigma((pred(y)-y)^2)/m
RMSE = np.sqrt(np.array(mse).mean())MAE/RMSE需要结合真实值的量纲才能判断差异。
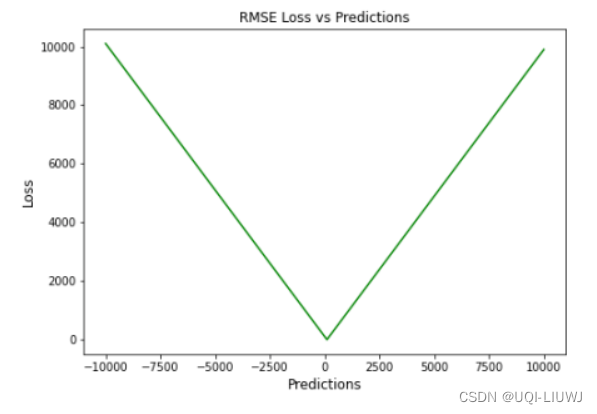
2.1 RMSE与MAE的对比
RMSE相当于L2范数,MAE相当于L1范数。
次数越高,计算结果就越与较大的值有关,而忽略较小的值。
所以这就是为什么RMSE针对异常值更敏感的原因(即有一个预测值与真实值相差很大,那么RMSE就会很大)。
最小化 MAE 的预测方法将导致预测中位数,而最小化 RMSE 将导致预测均值。
相对来说,MAE和MAPE不容易受极端值的影响;而MSE/RMSE采用误差的平方,会放大预测误差,所以对于离群数据更敏感,可以突出影响较大的误差值。
2.2 缺点
- RMSE仍然是一个线性平分函数,所以梯度在最小值附近是突变的
- 随着误差幅度的增加,RMSE 对异常值的敏感性也随之增加
3 SD
- Standard Deviation ,标准差
- 是方差的算数平方根

4 MSE
- Mean Squared Error,均方误差
-

- 当误差被平方时,离群值被赋予更多的权重。受益于这种对离群 Loss 的惩罚,有助于优化算法获得参数的最佳值
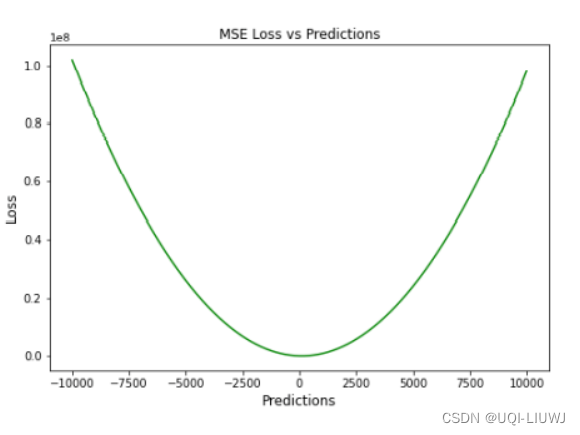
4.1 优缺点
优点:
- 在prediction接近ground-truth的时候,梯度会逐渐减少
- ——>有助于对微小错误进行有效的最小收敛
- 用二次方程表示,有助于在异常值的情况下调整模型参数。
缺点
- 较高的损失值可能会导致反向传播过程中的大幅跳跃
- 对异常值特别敏感,这意味着数据中的显著异常值可能会影响模型性能
5 MAPE
- Mean Absolute Percentage Error 平均绝对百分比误差
- 范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
- 当真实值有数据等于0时,存在分母0除问题,该公式不可用!
How to calculate MAPE with actual values at or close to 0 (stephenallwright.com)
for x, y in data_iter:y=model(x)d = np.abs(y - y_pred)mape += (d / y).tolist()#mape=sigma(|(pred(x)-y)/y|)/m MAPE = np.array(mape).mean()
这边说的percentage error就是 Σ里面不带绝对值的部分
百分比误差具有无单位的优势,因此经常用于比较数据集之间的预测性能。
基于百分比误差的度量的缺点是,如果 对于评估的时间片期间的任何 t,yt=0 。则这一个PE为无穷大,如果任何 yt 接近于零,则具有极端值。
另外一个缺点是,MAPE对正Loss的惩罚小于负Loss。因此,当我们比较预测算法的精度时,它是有偏差的。
6 SMAPE
- Symmetric Mean Absolute Percentage Error 对称平均绝对百分比误差

- 当真实值有数据等于0,而预测值也等于0时,存在分母0除问题,该公式不可用!
7 sklearn实现
sklearn 笔记整理:sklearn.mertics_UQI-LIUWJ的博客-CSDN博客
8 scaled error
在比较具有不同单位的时间序列的预测准确性时,提出了比例误差scaled error作为PE percentage error的替代方法。
- 对于非季节性时间序列,一种有用的方法是定义一个naive的预测方法,来计算比例误差
因为分子和分母都涉及原始数据尺度上的值,所以 qj 与数据尺度无关。
如果一个比例误差是由 比naive预测更好的预测产生的,则qj小于 1。
相反,如果预测比naive预测更差,则qj大于 1。
- 对于季节性数据,我们可以:使用一个季节性naive预测方法,来达到同样的效果:

8.1 MASE mean absolute scaled error
参考内容:2211.02989.pdf (arxiv.org)
A Comprehensive Survey of Regression Based Loss Functions for Time Series Forecasting
9 MBE mean bias error
- 平均偏差误差 (MBE)
- 正偏差表示数据误差被高估,而负偏差表示误差被低估
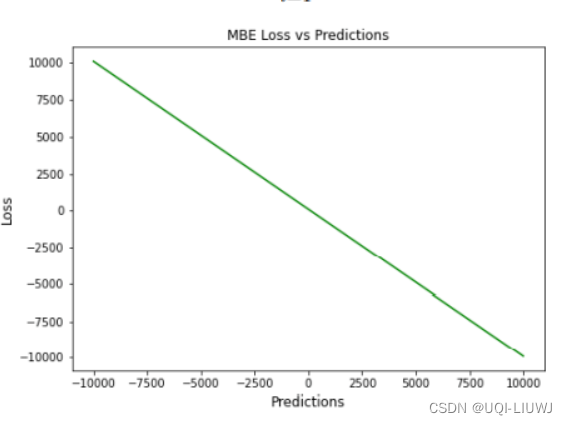
9.1 优缺点
优点
- 确定模型误差的方向
缺点
- 误差往往会相互抵消,不是一个合适的损失函数
10 RAE
将总绝对误差除以平均值与实际值之间的绝对差值
,其中
接近零代表模型良好。
11 RSE
,其中