位运算位与

article/2025/8/27 10:15:30

一、知识点

1.位与的定义

2.简单应用

（1）奇偶性判定

（2）取末五位

(3)消除末尾五位

（4）2的幂判定

二、习题

1.191. 位1的个数 - 力扣（LeetCode）

2.剑指 Offer 15. 二进制中1的个数 - 力扣（LeetCode）

3. 1356. 根据数字二进制下 1 的数目排序 - 力扣（LeetCode）

4.762. 二进制表示中质数个计算置位 - 力扣（LeetCode）

5.231. 2 的幂 - 力扣（LeetCode）

6.397. 整数替换 - 力扣（LeetCode）

7.1404. 将二进制表示减到 1 的步骤数 - 力扣（LeetCode）

一、知识点

1.位与的定义

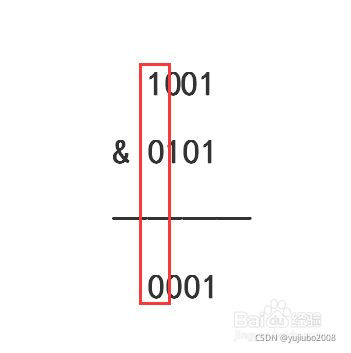
位与运算符有两个操作数，表示为 x & y

对操作数的每一位进行运算，都是1的时候结果为1，否则为0

左操作数	右操作数	结果
0	0	0
0	1	0
1	0	0
1	1	1

举例：0b1010&0b0110=0b0010；（0b为二进制数前缀）

（printf设置输出结果%d为十进制数2）

2.简单应用

（1）奇偶性判定

if(5%2==1)
{cout<<"5是奇数";}if(5&1)              //5&1==1
{cout<<"5是奇数";}if(8&1==0)              
{cout<<"8是偶数";}

偶数二进制末位为0，奇数二进制末位为1。

偶数&1为0，奇数&1为1，即可判断。

（2）取末五位

//给定一个数，求它的二进制表示的末五位，以十进制输出即可。#include<iostream>
using namespace std;
int main()
{int x;cin>>x;cout<<(x&0b11111)<<endl;return 0;
}

问题核心：我们只需要末五位，剩下的位不需要，所以将给定的数位与 0b11111 ，这样可以直接得到末五位的值，因为11111再高位为0，不管是0还是1 位与 0 都是0，即可将高位抹去，而末五位，0&1=0，1&1=1，也就是说末五位位与 11111的结果是不变的，仍然是末五位。

(3)消除末尾五位

给定一个32位整数，要求消除它的末五位。

消除末五位，即将末五位变成0，保留剩下的位

将这个数与0b 11111111111111111111111111100000 （转换成十六进制为0xffffffe0）位与。

x&0b11111111111111111111111111100000 与 x&0xffffffe0 同理。

（4）2的幂判定

判断一个整数是不是2的幂

如果一个数是2的幂，它的二进制必然为 100……00 形式。(有k个0）这个数的十进制为 $2^{k}$

将其减一，二进制表示为011……11形式（有k个1）（可根据等比数列的和的公式来推导）

这两个数位与为0，

所以一个数x是2的幂，那么x&(x-1)必然为0。

(x&(x-1))==0

二、习题

1.191. 位1的个数 - 力扣（LeetCode）

class Solution {
public:int hammingWeight(uint32_t n) {int sum=0;
while(n)
{
n&=(n-1); 
sum++;
}return sum; }
};
//若一个数末尾有k个0（末尾的前面是1：100……00），将它减1，错位可得k个1（前面为0：011……11） 两者位运算得到k+1个0，将数的最低位1去掉。
//n & (n-1) 实现：将n的二进制最低位的1去掉，去掉多少次，就有多少1。
//若末尾为1，它减1，末尾为0，其他位数一样，两者位与，1仍然消去仍然可以n&(n-1)

2.剑指 Offer 15. 二进制中1的个数 - 力扣（LeetCode）

与1同理。

3. 1356. 根据数字二进制下 1 的数目排序 - 力扣（LeetCode）

题目：给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。

如果存在多个数字二进制中 1 的数目相同，则必须将它们按照数值大小升序排列。

请你返回排序后的数组。

class Solution {
public:
int bitcount(int n)   //1的数目
{
int sum=0;
while(n)
{
n&=(n-1);
sum++;
}
return sum;
}vector<int> sortByBits(vector<int>& arr) {for(int i=0;i<arr.size();i++)
{
arr[i]+=bitcount(arr[i])*100000;   //arr里所有数值更新为  它本身 + 1的数目*100000（不能是10000，因为10000%10000为0，只要是大于10^5的数里面只有一个1就行1000000也可以），给这个数升序，即满足题意。题目先根据1的数目排序，所以数目乘以100000，这个是排序第一个要考虑的，最高位的值，然后若1的数目一样，再根据数值本身，这样  arr[i] + 1的数目*100000 即满足条件。
}//造出 「1的个数 * 100000 + 原数字」的数字来排序。即高位数字表示1的个数，低位数字表示原数字。sort(arr.begin(),arr.end());   //arr数组升序。for(int i=0;i<arr.size();i++)
{
arr[i]%=100000;//最后将高位都去掉，留下arr[i]最初本身的数值。
}
return arr;}
};

4.762. 二进制表示中质数个计算置位 - 力扣（LeetCode）

给你两个整数 left 和 right ，在闭区间 [left, right] 范围内，统计并返回计算置位位数为质数的整数个数。

计算置位位数就是二进制表示中 1 的个数。

例如， 21 的二进制表示 10101 有 3 个计算置位。

class Solution {
public://是否为质数。
bool isprime(int n)
{if(n<2)return false;
for(int i=2;i<=sqrt(n);i++)
{
if(n%i==0)
return false;
}
return true;
}//数位中1的个数。这里面i数值的改变不影响for循环里，范围在left~right里的i的数值。 这个函数的代码若写在for里面，一定要注意i的值是改变的，应该要初始化一个中间变量，比如mid=i，来代替i判断i的个数是否为质数。
int bitcount(int i) 
{int num=0;
while(i)
{i&=(i-1);num++;//num为1的个数。
}
return num;
}int countPrimeSetBits(int left, int right) {
int sum=0,num;
for(int i=left;i<=right;i++)
{//判断num是否为质数。
if(isprime(bitcount(i))) //判断1的个数是否为质数。
sum++;
}return sum;}
};

5.231. 2 的幂 - 力扣（LeetCode）

class Solution {
public:bool isPowerOfTwo(int n) {
if(n<=0)
return false;if((n&(n-1))==0)
return true;return false;}
};

6.397. 整数替换 - 力扣（LeetCode）

给定一个正整数 n ，你可以做如下操作：

如果 n 是偶数，则用 n / 2替换 n 。
如果 n 是奇数，则可以用 n + 1或n - 1替换 n 。
返回 n 变为 1 所需的最小替换次数。

class Solution {
public:int integerReplacement(int n) {if(n==1)return 0;if(n%2==0)return 1+integerReplacement(n/2); 
//1步，n/=2return 2+min(integerReplacement(n/2),integerReplacement(n/2+1)); 
//两步，因为一个奇数+1，-1之后肯定要除以2， 
//n的最大值为2^31-1，若+1，则溢出，所以先对n除以2，再+1，
//floor(n/2)+1 等效于 (n+1)/2    floor(n/2) 等效于 (n-1)/2   floor为向下取整。}
};