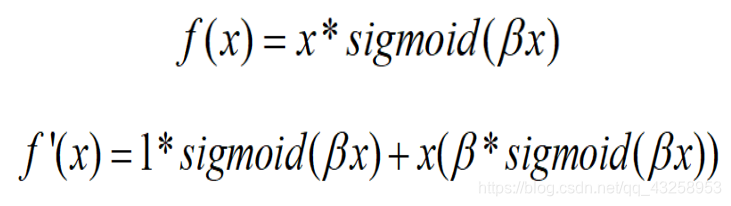
当β = 0时,Swish变为线性函数f(x)=x/2
β → ∞, σ(x)=(1+exp(−x))−1σ(x)=(1+exp(−x))−1为0或1. Swish变为ReLU: f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数. beta是个常数或者可以训练的参数。其具有无上界有下界、平滑、非单调的特性。其在模型效果上优于ReLU。


hard-Swish介绍
虽然这种Swish非线性提高了精度,但是在嵌入式环境中,他的
Swish hard-Swish
article/2025/9/18 20:07:55
相关文章
Lua整合工具 squish使用方法
squish是一个开源的用于打包lua脚本的小工具,它的主要功能是将多个lua文件整合成一个文件,并在此基础上做压缩和混淆等处理,混淆和压缩后的代码可以直接被执行而不需要先做解压还原等操作。
它的github地址:https://github.com/L…
测试资深人士推荐的GUI跨平台自动化测试工具
Squish GUI 测试自动化工具使跨平台测试应用程序变得容易,它对Qt的支持非常好。
在发布应用程序之前测试用户界面比以往任何时候都更加重要,当今用户需要从移动、桌面、Web和嵌入式应用程序中获得无缝的跨平台体验。由于应用程序经常在工厂、汽车甚至厨…
难道真的有人因为要分享squish测试工具而去学习QT吗
1下载安装
1.去官网下载QT工具并安装,下载地址:https://download.qt.io/official_releases/qt/ ;如下图选择自己想要下载的版本,我下载的5.12.12,文件3.7G,如图注册完成,全选完成,后…
UCSC 基因组浏览器配置详解
一、配置参数
UCSC基因组浏览器:传送门
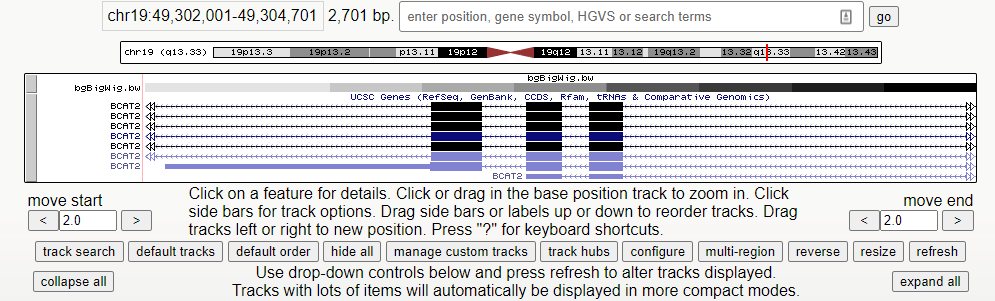
1、点击配置 2、进入配置页面:
点击刚刚运行的文件 BedGraph Format 2、轨迹配置页面 Type of graph :默认以bar,条形图来显示,选择point会以点或线来显示Track height &…
Squish — 基于Qt的HMI自动化测试工具
目录 自动化测试方案设置Squish记录测试属性验证视觉验证总结 本文翻译自Squish - Test automation tool for our HMI build with Qt 原文作者:Piotr Lesiecki 校审:Kenny Zhang
当测试工程师们听到自动化测试时,首先会想到的一定是Selenium…
Squish - GUI Tester
Squish - GUI Tester
Squish overview
网上查询关于自动化测试工具Squish的资料很少。特别是中文搜索。最近正好在使用这款工具,在使用中总结了一些知识,在这里和大家一起分享下。
Squish是froglogic公司的一款商业自动化工具,几年前好像是…
Squish for Qt:为Qt应用量身打造的自动化测试工具
转载地址:https://mp.weixin.qq.com/s?__bizMzI5MzA3NzU3OA&mid2649661399&idx1&sn7b584cfc54e529d6ce605274d8f7bc0b&chksmf46da8f2c31a21e4eccfe9ee0eb690045cdd8a074af0e57bceb8f605c5fcb2fb72c9d7334c28&mpshare1&scene1&srcid072…
基于GUI测试工具Squish的使用
转载自:http://www.readingday.cn/squish-for-qt-2/ 申请Squish试用 浏览器打开Squish官网(https://www.froglogic.com/squish/free-trial/),填写试用申请表。您需要提供一个有效的邮箱地址,以便接收到Squish官方所发送…
浅析如何利用Squish实行 GUI自动化测试
1.引言 图形用户界面(Graphical User Interface,简称 GUI,又称图形用户接口)是指采用图形方式显示的系统操作用户界面。是软件与用户进行交互的主要方式,与早期计算机使用的命令行界面相比,图形界面对于用户…
关于Squish的介绍和简单使用说明
网络研讨会 | Squish for Qt: 为Qt应用量身打造的自动化测试工具_哔哩哔哩_bilibiliSquish是一款跨平台、支持多种开发技术的GUI自动化测试工具,基于对象识别的GUI自动化测试工具、支持各类操作系统、可为多种技术开发的应用程序提供GUI自动化测试。操作简单、脚本语…
3乘3魔方第四步_三阶魔方第四步
三阶魔方的第四步是顶棱翻色,首先转出黄色的顶层十字,将魔方顺时针旋转九十度,转到红色的一面,右边顺时针旋转九十度,将底层的白色面转动到上面,顶层再顺时针旋转九十度,右侧逆时针旋转九十度&a…
java还原三阶魔方_魔方小站四阶魔方教程2 一看就懂的魔方教程(魔方玩法视频教程+还原公式一步一步图解+3D动画)...
形成下图的样子, 这一步很简单,只需要学会一个很好理解的技术就行了,请看下面标准情况的例子,魔方 您可以用鼠标拖拽3D动画里的整个魔方,以看到魔方背面的变化。 TR U R U 我们要合并位于前面的这一对红白棱块 合并棱块。 将合并好的一对红白棱块转到右面。 旋转右面,你要…
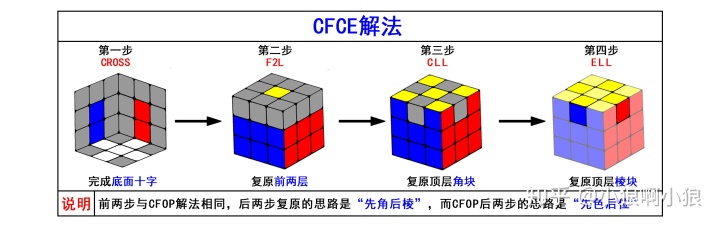
魔方cfop公式软件_【番外篇】八大魔方快速还原法图解介绍汇总大全!
本篇在上一篇文章的基础上,主要介绍目前魔方圈主流的速拧还原解法。 本篇文章仅介绍主流的快速还原法即 速拧解法,不包括其他初级玩法等,初级玩法也很多(笑面虎、8355、棱先、角先等等),甚至有些独立还原者能创造属于自己的解法,有些解法思路巧妙,有些解法容易上手,总…
二阶魔方还原 - 4步2公式
三阶魔方的公式记录在 https://blog.csdn.net/Bob__yuan/article/details/86546920,这是只需要记7个公式就可以三阶魔方还原法,本文为二阶魔方“傻瓜还原法”,即不需要另外再记公式,只需要会上述三阶魔方中的2个公式就可以还原的方…
UTF-8转码GBK
昨天一个大学的同学问了一个关于utf-8转码gbk的问题,所以两个人一起讨论了一下关于utf-8转码成为GBK的乱码原因。 正常情况下如果我们需要将UTF-8格式转码为GBK,我们会需要经过这样一个中转: 通常情况下如果直接转码会出现一种情况就是GBK转码…
python常用英语词汇(持续更新)
✅作者简介:大家好我是hacker707,大家可以叫我hacker 📃个人主页:hacker707的csdn博客 🔥系列专栏:python 💬推荐一款模拟面试、刷题神器👉点击跳转进入网站 一直有人问我,自己英语不…
Python常用英文单词【最强总结】
嗨嗨,我是小圆,总有人在刚了解到python的时候,会考虑一个问题
英语不好能学好python吗?
当然可以,学习python用到的单词并不是很多。 今天就给大家分享一下Python常用英文单词。
一、交互式环境与print输出
1、pr…
史上最全python常用英语单词,建议收藏
于刚才是学习python这些也足够了,一天学个六七个单词记一下在配合自己寻找的视频、书籍等等方法去学习是有一定帮助的。 这里还是要说一句,仅供兴趣爱好学习使用,个人开发者(非考虑未来靠此为生的人士)我们一起学习,一起成长。 下列常用单词大家可以复制一下,自己用Word…