图像中的角点是图像的重要特征, 具有旋转不变性, 决定了图像形状, 可以降低图像信息的存储效率, 在目标跟踪, 目标检测, 图像匹配, 图像轮廓拟合等领域都有重要的应用价值. 近几十年来, 国内外学者提出的图像角点检测算法[, 各有各的优缺点, 大致可分为三大类: 基于灰度强度的角点检测、基于模型的角点检测、基于边缘轮廓的角点检测[. 基于灰度强度的方法是通过图像的一阶或二阶导数查找, 经典算法代表有Harris算法[, Harris算法通过微分运算和自相关矩阵来检测角点, 稳定性高, 但是高斯平滑函数的窗口可控性差, 定位精度较差[.基于模型的方法是通过将一小块图像与预定义的模型相匹配来查找角点, SUSAN算法[就是这类角点检测的代表, SUSAN通过一个圆形模板实现角点检测, 通过模板中所有与圆心点像素相似的点组成的区域大小判断角点, 该算法不对图像求导, 精度较好, 具有一定的抗噪性, 但是相似函数计算较复杂, 且需要人工设定阈值[. 基于边缘轮廓的方法主要是通过分析图像边缘形状来检测角点的, 包括五个步骤[: 边缘提取和选择、曲线平滑、曲率估计、检测角点和角点跟踪筛选出最终的角点. 近年来, 基于边缘轮廓方法吸引了广泛的关注, 许多此类优秀的角点检测算法被提出[. 1998年Mokhtarian等人提出的著名CSS角点检测算法[, 利用Canny边缘检测算子提取图像边缘, 从边缘中提取边缘轮廓, 并填充边缘轮廓缺口, 在大尺度下得到轮廓曲率极大值点, 通过阈值选定候选角点, 大尺度到小尺度下对候选角点重新定位, 比较T-角点与曲率极大值检测的角点, 剔除相距相近的点, 该算法获得良好的角点检测效果. 但CSS有两个主要的问题[, 一是曲率估计对对轮廓局部变化和噪声较为敏感, 二是很难选择合适的高斯尺度平滑边缘轮廓. 在CSS基础上, 通过考虑检测中局部曲率, He和Yung[提出了一种使用自适应曲率阈值和动态支撑区域的检测器. 随后Awrangjeb和Lu利用点到弦的距离累加技术提出了一种稳健的角点检测算法——CPDA[, CPDA具有较高的可重复性和较低的定位误差. 之后又提出了CPDA的快速算法[. 但CPDA有一个缺点是估计拐角的曲率值与角度可能不成正比[. 还有一些角点检测算法, 利用Freeman链码多边形近似方法查找角点, 两边的交点判定为角点[, 文献[
本文在文献[
1 Freeman链码生成
1.1 图像预处理
本文图像在预处理方面与文献[[检测边缘, Canny算法抑制了多响应边缘, 提高边缘的定位精度, 具有一定的抗噪能力. Canny算法检测边缘的步骤如
图 1
Fig. 1
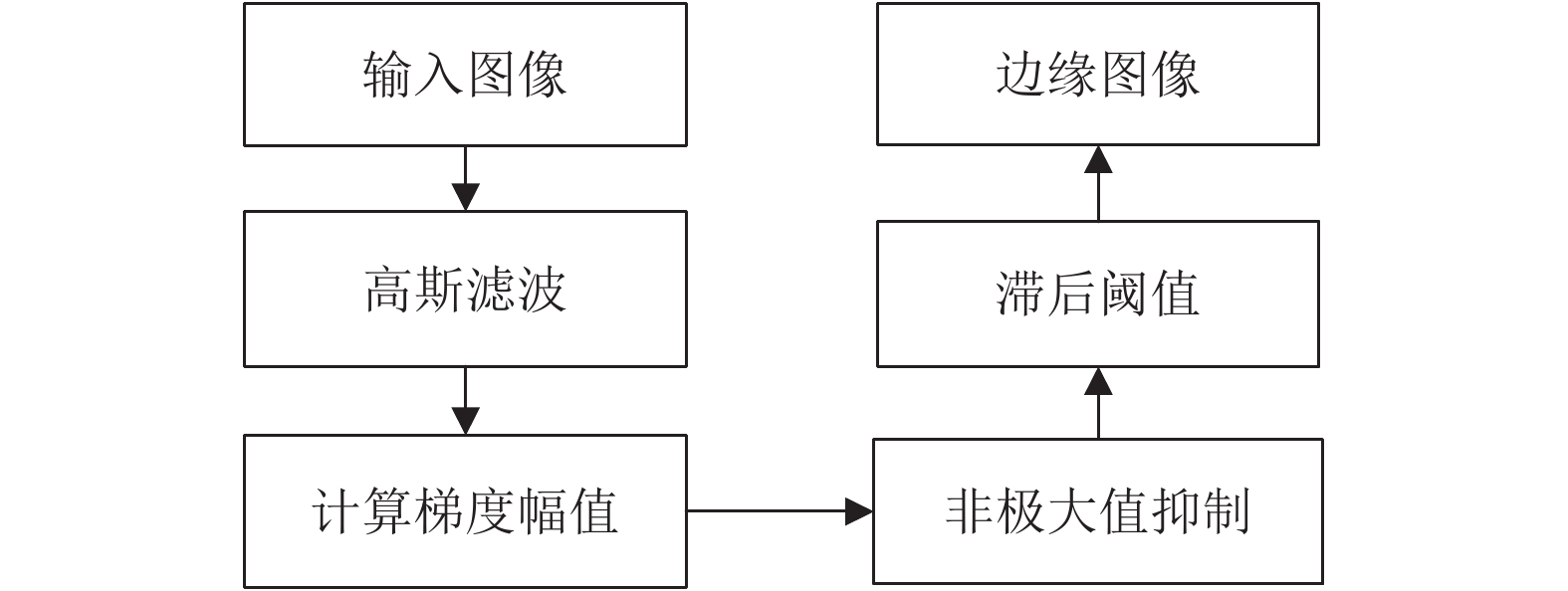
图 1 Canny边缘检测步骤
1.2 Freeman链码
链码是通过带有给定方向的单位长度的线段序列来描述轮廓的边界, 链码的表示方法有基于4-邻接和8-邻接[, 如[产生轮廓的链码, 4-邻接检测边界只需要搜索4个方向, 8-邻接则需要搜索8个方向, 我们实验所用图都是点阵图, 当轮廓是一条直线时, 4-邻接链码要比8-邻接链码要快捷的多; 当轮廓是一条斜边时, 用4-邻接链码只能搜索上下左右4个方向, 表示轮廓时会丢失大量的边缘信息, 而8-邻接链码正好与像素点的实际情况相符, 能够准确地描述中心像素点与其邻接点的信息, 能较好地保留轮廓边缘信息. 因为任意一个像素周围均有8个邻接点, 因此本文算法采用的是8-邻接链码.
图 2
Fig. 2
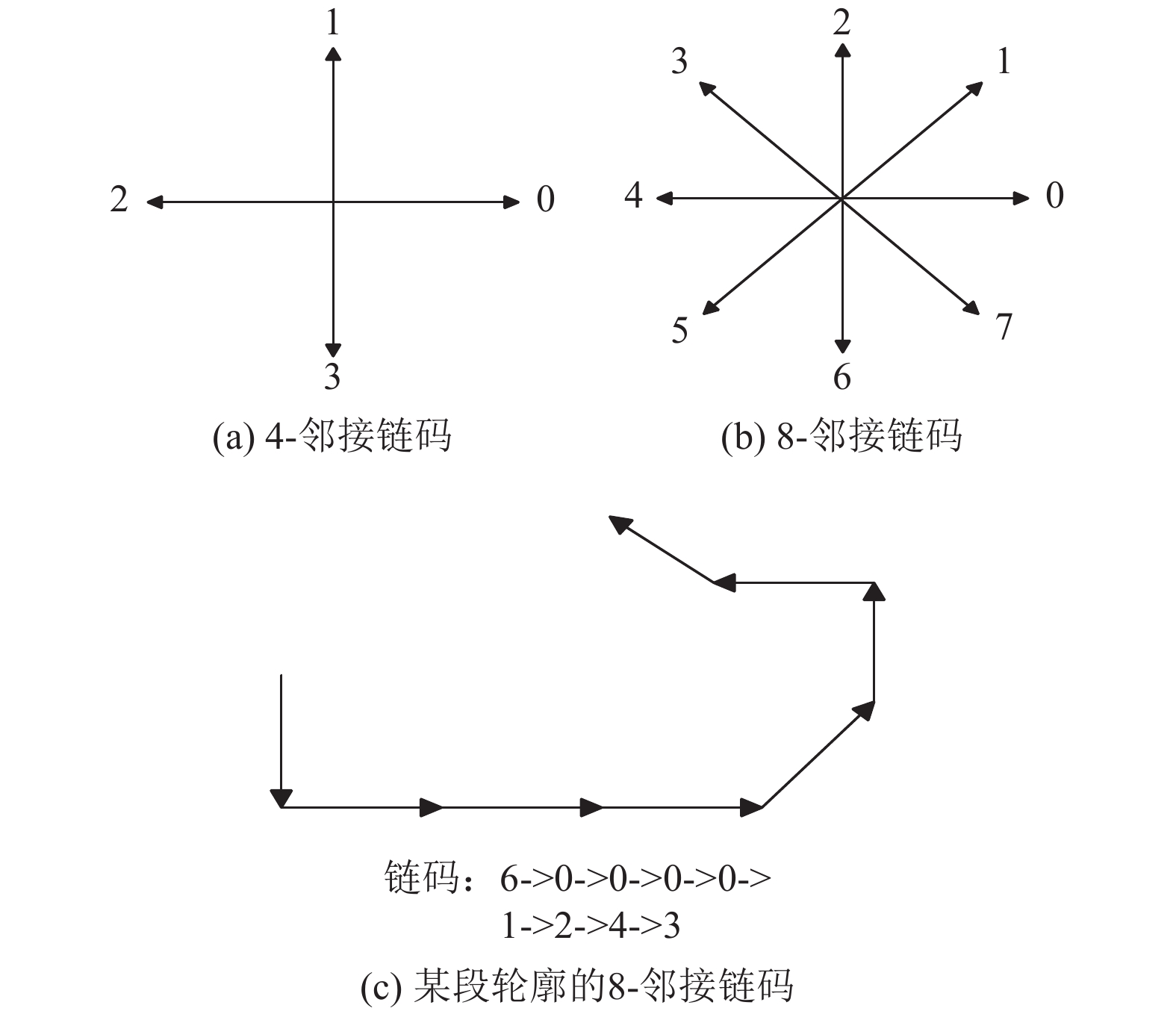
图 2 链码示意图
一条轮廓曲线Freeman链码可以定义为:
${\left\{ {{a_{i - 1}} \to {a_i}} \right\}^n}$, 其中
${a_i} \in \left\{ {0,1,2,3,4,5,6,7} \right\}$, n表示轮廓点集数. 如
1.3 轮廓跟踪得到Freeman链码
基于八邻域边界跟踪可以得到轮廓的Freeman链码, 轮廓跟踪[方法如算法1.
算法1. 轮廓跟踪生成Freeman链码算法.
1) 分轮廓搜索, 找到图像最左上角的一个边界轮廓点P0作为搜索起点, 并以链码值dir=0为最开始搜索方向;
2) 按八邻域的逆时针方向搜索起点的下一个点, 每搜索一次链码值方向逆时针旋转45°, 即dir+1; 如果搜索到新的边界点Pi, 将该链码值赋值给它前一个点即点Pi–1的方向, 再以此点为八邻域的中心点, 链码值方向顺时针旋转90°, 即dir–2作为该点的开始搜索方向, 继续搜索;
3) 重复2)搜索方法, 当搜索到起始点P0时, 整个轮廓搜索完毕.
通过上述轮廓跟踪算法就得到了边缘轮廓的Freeman链码, 我们假定逆时针为正方向, 分轮廓将轮廓点坐标和链码值存储, 存储FMP格式有如下的定义:
struct FMP
{
int x; //点的图像x坐标
int y; //点的图像y坐标
int a; //下一个点的方向
}
2 对Freeman链码方向分析进行角点