OJ算法分析题库（2）

article/2025/10/8 8:49:21

P1476 加工生产调度

【实验】贪心算法之流水作业调度问题（分析）

P1748 a+b+c+d==0

P1750 求逆序对

P1746 求解查找最后一个数小于等于指定数的元素问题

P1477 部分背包问题（分析）

算法分析：

算法大致的思路就是通过四个数组分别存储每次输入的数值内容。然后通过分组循环，四个数分两组，a和b一组进行一对多依次加法存到数组中，保证每个a组的数都和b组中的所有数进行过了加法运算。c和d也是一样的方式。

两个数组ab和cd运算完毕以后，进行排序。排序完成以后接下来通过对ab数组的值进行依次循环，然后每次都会cd数组也进行循环判断，找到ab+cd=0的情况的个数。为了应对数值相同的情况，这里用到了upper_bound和lower_bound两个函数进行运算，具体原理读者可以自行分析。总之经过如上的运算，最终可以得到相应的个数。

这里是相应的算法。来源于网络，算法非原创，分析为原创，仅供学习使用，如果侵权请告知删除

/** @Description: To iterate is human, to recurse divine.* @Autor: Recursion* @Date: 2022-03-23 09:44:28* @LastEditTime: 2022-03-23 12:03:40*/
#include<bits/stdc++.h>
using namespace std;
int T,n,sum;
int a[10000],b[10000],c[10000],d[10000];
int ab[200000001],cd[200000001];
// int a[10000][10000];// void read()
// {
//     for(int i = 1;i <= n;i ++)
//         for(int j = 1;j <= 4;j ++)
//             cin >> a[i][j];
// }
// void dfs(int x)
// {
//     if(x == 4 + 1){
//         if(sum == 0)
//             ans++;
//         return;
//     }
//     for(int i = 1;i <= n;i ++){
//         sum += a[i][x];
//         dfs(x + 1);
//         sum -= a[i][x];
//     }// }// int main()
// {
//     cin >> T;
//     while(T--){
//         cin >> n;
//         read();
//         dfs(1);
//         cout << ans << endl;
//     }
// }void read()
{for(int i = 0;i < n;i ++)cin >> a[i] >> b[i] >> c[i] >> d[i];
}void solve()
{for(int i = 0;i < n;i ++)for(int j = 0;j < n;j ++){ab[i*n + j] = a[i] + b[j];cd[i*n + j] = c[i] + d[j];}sort(ab,ab + n*n);sort(cd,cd + n*n);long long int ans = 0;for(int i = 0;i < n*n;i ++){int temp = -ab[i];ans += upper_bound(cd,cd + n*n, temp) - lower_bound(cd,cd + n*n,temp);}/*upper_bound(first, last, val) 寻找在数组或容器的[first,last)范围第一个大于val的元素位置lower_bound(first, last, val)寻找在数组或容器的[first,last)范围第一个大于等于val的元素位置使用时必须为有序的数组或容器相减得到相等个数lower_bound：功能：查找非递减序列[first,last) 内第一个大于或等于某个元素的位置。返回值：如果找到返回找到元素的地址否则返回last的地址。（这样不注意的话会越界，小心）用法：int t=lower_bound(a+l,a+r,key)-a；(a是数组)。upper_bound:功能：查找非递减序列[first,last) 内第一个大于某个元素的位置。返回值：如果找到返回找到元素的地址否则返回last的地址。（同样这样不注意的话会越界，小心）用法：int t=upper_bound(a+l,a+r,key)-a；(a是数组)。*/cout << ans << endl;
}int main()
{int t;cin >> t;while(t--){cin >> n;read();solve();}
}

 这题就是一道比较简单的求逆序数的问题。

算法1：暴力比较法 两次循环比较 时间复杂度是n平方 时间浪费很多

#include<iostream>
using namespace std;
int numbers=0;
void getresult(int a[],int start,int n){if(start==n-1)return;for(int i=start+1;i<=n-1;i++){if(a[start]>a[i])numbers++;}
}
int main(){int n;cin>>n;int a[n];for(int i=0;i<n;i++)cin>>a[i];for(int i=0;i<=n-2;i++)getresult(a,i,n);cout<<numbers<<endl;return 0;
}

 这里为了节省时间 我们不妨考虑借助二路归并排序的思想 进行分治法的求逆序数

（但是oj判断Runtime error 不清楚为什么 待解决）

#include<iostream>
int numbers=0;
using namespace std;
void getnumber(int a[],int low,int mid,int high){int i=low;int j=mid+1;int k=0;int tmp[100];while(i<=mid && j<=high){if(a[i]>a[j]){numbers+=mid-i+1;tmp[k++]=a[j++];}	else tmp[k++]=a[i++];}while(i<=mid) tmp[k++]=a[i++];while(j<=high) tmp[k++]=a[j++];for(int k1=0;k1<k;k1++)a[low+k1]=tmp[k1];
}
void Merge_sort(int a[],int low,int high){if(low<high){int mid=(low+high)/2;Merge_sort(a,low,mid);Merge_sort(a,mid+1,high);getnumber(a,low,mid,high);}	
}
int main(){int n;cin>>n;int a[n];for(int i=0;i<n;i++)cin>>a[i];Merge_sort(a,0,n-1);cout<<numbers<<endl;return 0;
}

这里再提供一个通过oj判断的算法

#include <bits/stdc++.h>
using namespace std;#define ll long long
#define lson l,mid,tree[rt].l
#define rson mid+1,r,tree[rt].r
#define ls tree[rt].l
#define rs tree[rt].rconst int mac=5e5+10;
const int inf=1e9+5;struct node
{int l,r,sum;
}tree[mac*32];
int sz=1;//动态分配的点的最大编号ll query(int l,int r,int rt,int L,int R)
{ll ans=0;if (l>=L && r<=R){return tree[rt].sum;}int mid=(l+r)>>1;if (mid>=L) ans+=query(lson,L,R);if (mid<R) ans+=query(rson,L,R);return ans;
}void update(int l,int r,int &rt,int pos)
{if (!rt) rt = ++sz;//如果说这个节点不存在，我们就将节点数+1，当前节点为最大最大节点，和主席树有点类似，而这也是动态开点的核心if (l==r) {tree[rt].sum++;return;}int mid=(l+r)>>1;if (mid>=pos) update(lson,pos);//注意这里传进去的rt是左儿子的编号else update(rson,pos);tree[rt].sum=tree[ls].sum+tree[rs].sum;
}int main()
{int n;scanf ("%d",&n);ll ans=0;int root=1;for (int i=1; i<=n; i++){int x;scanf ("%d",&x);ans+=query(1,inf,1,x+1,inf);update(1,inf,root,x);}printf ("%lld\n",ans);return 0;
}

 借助二分查找排序的思路进行递归比较 这样时间复杂度低 浪费的时间少

#include<bits/stdc++.h>
using namespace std;
void functions(int a[],int b[],int n,int m){for(int i=0;i<m;i++){int l=0,r=n-1,mid;while(l<=r){mid=(l+r)/2;if(a[mid]<=b[i]) l=mid+1;else r=mid-1;}b[i]=a[r];}
}
int main(){int n,m,i;cin>>n>>m;int a[n],b[m];for(i=0;i<n;i++) cin>>a[i];for(i=0;i<m;i++) cin>>b[i];functions(a,b,n,m);for(i=0;i<m;i++) cout<<b[i]<<endl; return 0;
}

自行编写：

#include<bits/stdc++.h>
using namespace std;
void fun(int a[],int b[],int n,int m){for(int i=0;i<m;i++){  //外圈大循环 用于依次处理相应的待处理数据 b[i]即表示待测试数据 if(b[i]>=a[n-1]){ b[i]=a[n-1]; continue; }if(b[i]<a[0]) { b[i]=-1; continue; }if(b[i]==a[0]) { b[i]=a[0]; continue;}int left=0,right=n-1,mid;while(left<=right){mid=(right+left)/2;if(a[mid]<=b[i]) left=mid+1;else right=mid-1;} b[i]=a[right];}
}
int main(){int n,m; cin>>n>>m; int a[n],b[m];for(int i=0;i<n;i++) cin>>a[i];for(int j=0;j<m;j++) cin>>b[j];fun(a,b,n,m); for(int i=0;i<m;i++) cout<<b[i]<<endl; return 0;
}

 模型是经典的背包可分割问题 我们采用贪心算法即可完成

#include<bits/stdc++.h>
using namespace std;
struct NodeType{double weight;double value;double p;bool operator<(const NodeType &s) const{return p>s.p;}
};
int main(){int N,T,i;cin>>N>>T;double value=0.0;double x[N+1];NodeType A[N+1];for(i=1;i<=N;i++) {cin>>A[i].weight>>A[i].value;A[i].p=A[i].value/A[i].weight;}sort(A+1,A+N+1);//this is knap function below double weight_left=T;i=1;while(A[i].weight<weight_left){x[i]=1;weight_left-=A[i].weight;value+=A[i].value;i++;}if(weight_left>0){x[i]=weight_left/A[i].weight;value+=x[i]*A[i].value;}printf("%.2lf\n",value);return 0;
}

常见错误：

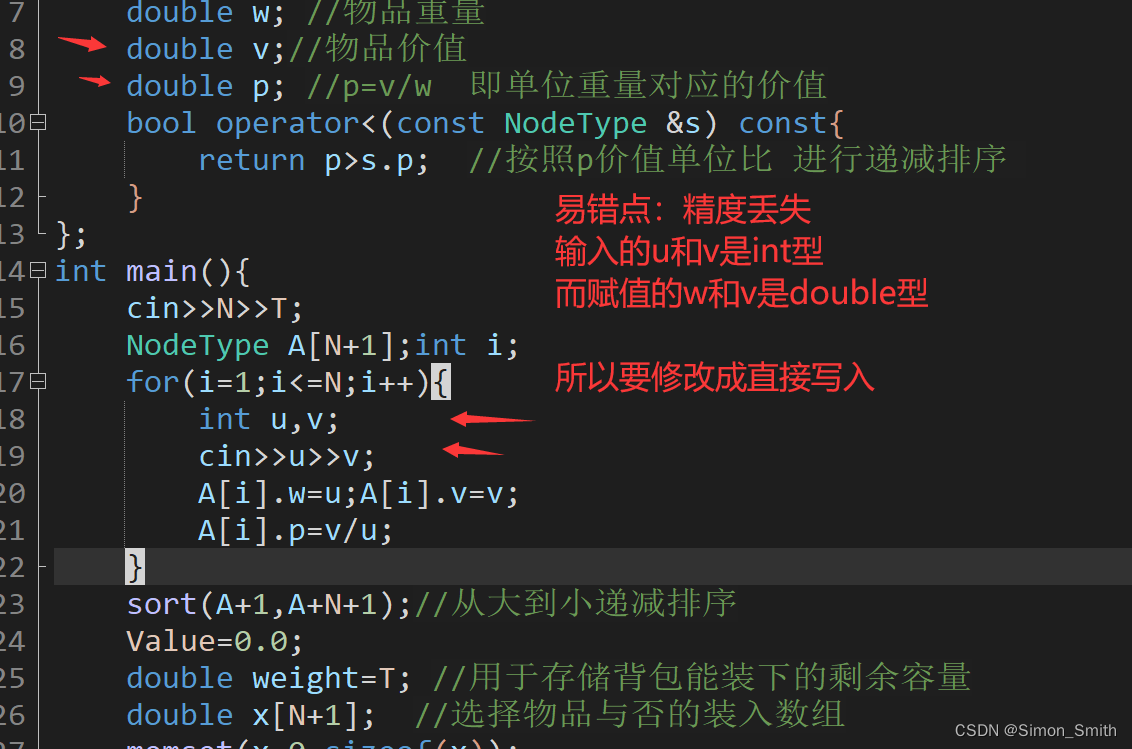
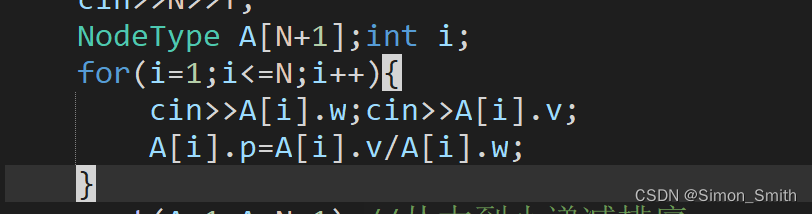 修改后的通关代码：

#include<bits/stdc++.h>
using namespace std;
//贪心算法 求解部分可分割背包问题
int N,T;  //N可以表示成背包数量  T可以理解成背包的容量 
double Value;  //用于存储总价值
struct NodeType{double w; //物品重量double v;//物品价值double p; //p=v/w  即单位重量对应的价值bool operator<(const NodeType &s) const{return p>s.p;  //按照p价值单位比 进行递减排序 } 
};
int main(){cin>>N>>T;NodeType A[N+1];int i; for(i=1;i<=N;i++){cin>>A[i].w;cin>>A[i].v;A[i].p=A[i].v/A[i].w;}sort(A+1,A+N+1);//从大到小递减排序Value=0.0;double weight=T; //用于存储背包能装下的剩余容量double x[N+1];  //选择物品与否的装入数组memset(x,0,sizeof(x));i=1;while(A[i].w<weight){x[i]=1;weight-=A[i].w;Value+=A[i].v;i++;} if(weight>0){  //如果余下重量大于0 说明没有装满x[i]=weight/A[i].w;Value+=x[i]*A[i].v;}printf("%.2lf\n",Value);return 0;	 
}

接下来是对这个问题的分析，会给出一些其他变化的算法形式。

贪心法可以用于求解背包问题中的可分割背包问题。

 

 

 

 

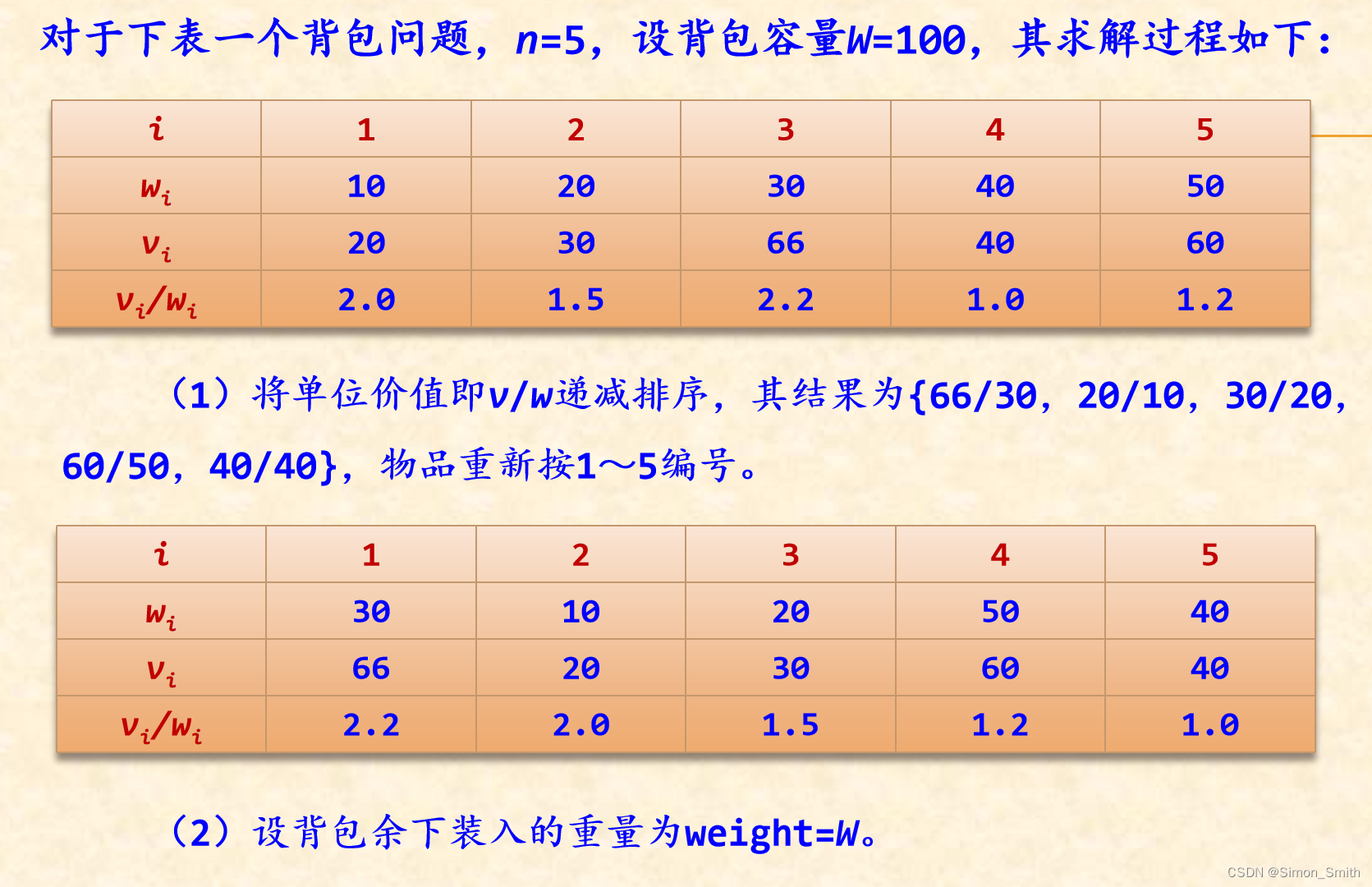
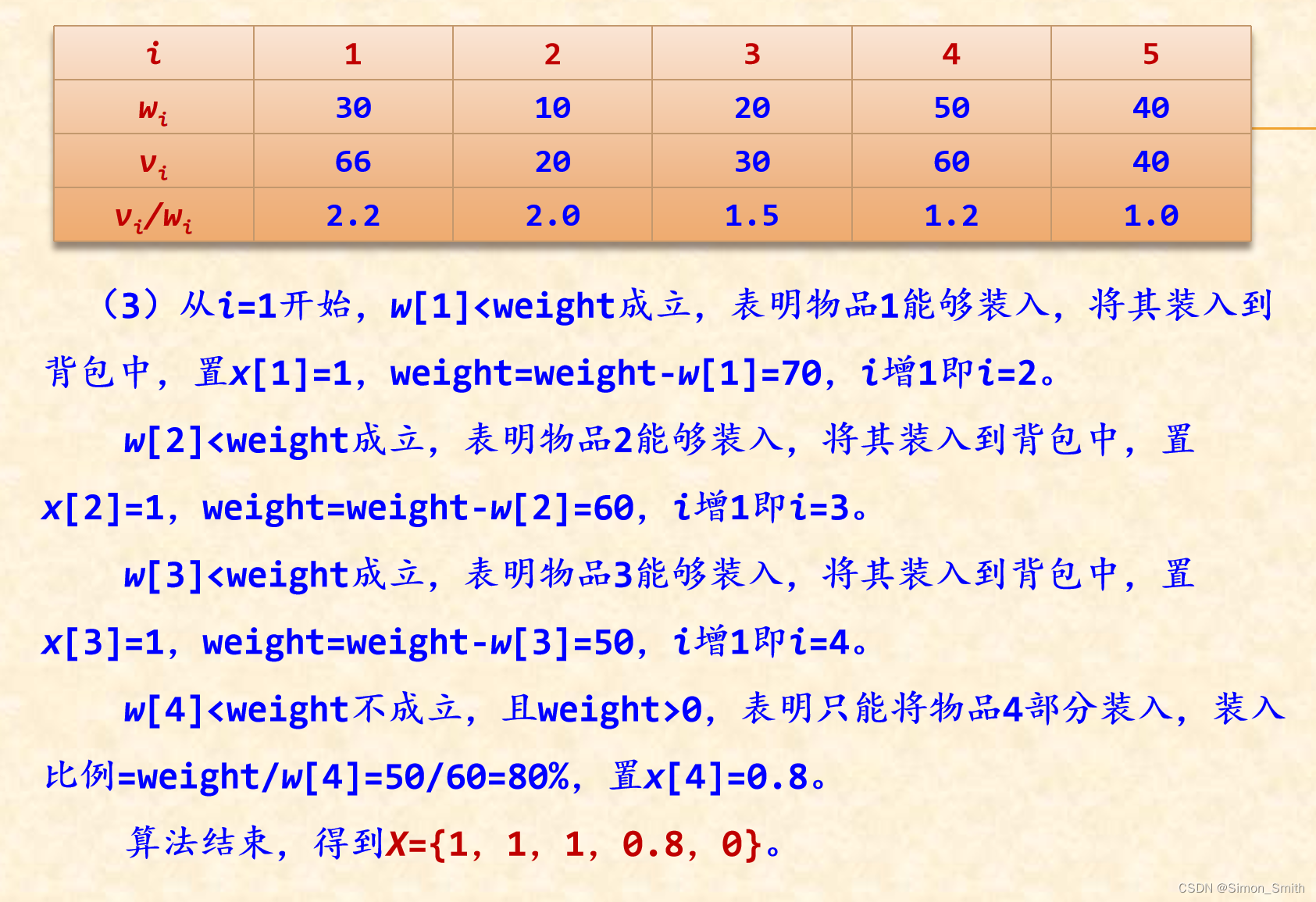
 参考代码部分：

//问题表示
int n=5;
double W=100;				//限重
struct NodeType
{  double w;double v;double p;				//p=v/wbool operator<(const NodeType &s) const{return p>s.p;			//按p递减排序}
};
NodeType A[]={{0},{10,20},{20,30},{30,66},{40,40},{50,60}};						//下标0不用
//求解结果表示
double V;				//最大价值
double x[MAXN];
void Knap()			//求解背包问题并返回总价值
{  V=0;				//V初始化为0double weight=W;		//背包中能装入的余下重量memset(x,0,sizeof(x));	//初始化x向量int i=1;while (A[i].w<weight)	//物品i能够全部装入时循环{  x[i]=1;			//装入物品iweight-=A[i].w;		//减少背包中能装入的余下重量V+=A[i].v;		//累计总价值i++;			//继续循环}if (weight>0)		//当余下重量大于0{  x[i]=weight/A[i].w;	//将物品i的一部分装入V+=x[i]*A[i].v;		//累计总价值}
}
void main()
{  printf("求解过程\n");for (int i=1;i<=n;i++)		//求v/wA[i].p=A[i].v/A[i].w;printf("(1)排序前\n");dispA();sort(A+1,A+n+1);			//A[1..n]排序printf("(2)排序后\n"); dispA();Knap();printf("(3)求解结果\n");		//输出结果printf("    x: [");for (int j=1;j<=n;j++)printf("%g, ",x[j]);printf("%g]\n",x[n]);printf("    总价值=%g\n",V);
}

针对这道OJ题，对该算法变形后得到的可以通关的算法如下：

 算法分析：这题属于贪心算法中常见的加工生产调度（流水作业调度问题）

可以贪心的思考这个例题最优解的情况。就是让A和B都马不停蹄的进行工作。所以A的选取优先原则是尽可能选择A耗时较少的，让B早点动工。同时也要让B优先加工时间长的，让A少一些等待

参考地址：

https://blog.csdn.net/weixin_42928870/article/details/81701061
https://www.likecs.com/show-460547.html

参考算法1：（时间复杂度会比较高）

#include<bits/stdc++.h>
struct Str { int w;int num;};
bool cmp(Str x, Str y){ return x.w < y.w; }
int main(){int n;while(scanf("%d", &n)){int a[1010], b[1010];Str s[5000];int u, v;int ans[1010];for(int k = 1;k <= n;k ++) scanf("%d", &a[k]); //读入for(int k = 1;k <= n;k ++) scanf("%d", &b[k]);for(int k = 1;k <= n;k ++) s[k].w = std::min(a[k], b[k]), s[k].num = k;std :: sort(s+1, s+n+1, cmp);//结构体存储，s[k].w表示用的时间. s[k].num 表示其序号u = 0, v = n+1;for(int k = 1;k <= n;k ++)if(s[k].w == a[s[k].num]) ans[++ u] = s[k].num;else  ans[-- v] = s[k].num;u = 0, v = 0;for(int k = 1;k <= n;k ++){u += a[ans[k]];if(v < u)  v = u;v += b[ans[k]];}printf("%d\n", v);}return 0;
}

参考算法2：

#include<bits/stdc++.h>
using namespace std;
const int N = 2005;
struct data {int id,a,b;
};
inline bool cmp(const data &A, const data &B) {//Jhonson不等式排序 return min(A.a, A.b) < min(B.a, B.b);
}
int main() {int n;while(scanf("%d", &n)){data J[N],ans[N];for(int i = 1; i <= n; ++i) {scanf("%d", &J[i].a);J[i].id = i;//原数组下标 }for(int i = 1; i <= n; ++i) scanf("%d", &J[i].b);sort(J + 1, J + 1 + n, cmp);for(int i = 1, p = 1, q = n; i <= n; ++i) {//p--队头 q--队尾 if(J[i].a <= J[i].b) ans[p++] = J[i];else ans[q--] = J[i];}int time1 = 0, time2 = 0;//time1--A机器上加工用时 time2--B机器上加工用时 for(int i = 1; i <= n; ++i) {time1 += ans[i].a;//第i件产品在A机器上所用时间 time2 = max(time1, time2);//在A机器上加工完才能到B机器 未加工完需要等待 time2 += ans[i].b;//第i件产品在B机器上所用时间 }printf("%d\n", time2);//最后一件在B机器加工完的时刻为结束时刻 //for(int i = 1; i <= n; ++i) printf("%d ", ans[i].id);//输出方案 	}return 0;
}

通关算法：

#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=1010;
struct node//三元组结构
{int id;//工作编号int ab;//在哪个机器int times;//时间bool operator < (node tmp)const{return times<tmp.times;//按时间从小到大排序}
};
void johnson(node s[],int n,int a[],int b[],int c[])//Johnson算法 生成三元组表s
{for(int i=1;i<=n;i++){if(a[i]>b[i])s[i].ab=2,s[i].times=b[i];elses[i].ab=1,s[i].times=a[i];s[i].id=i;}sort(s+1,s+n+1);//按times从下到大排序int l=0,r=n+1;for(int i=1;i<=n;i++)//生成加工顺序{if(s[i].ab==1)c[++l]=s[i].id;if(s[i].ab==2)c[--r]=s[i].id;}
}
int main()
{int n;while(cin>>n){int a[maxn],b[maxn],c[maxn],t[maxn];node s[maxn];for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)cin>>b[i];johnson(s,n,a,b,c);for(int i=1;i<=n;i++)计算最少时间 t[i]=t[i-1]+a[c[i]];int ans=t[1]+b[c[1]];for(int i=2;i<=n;i++)ans=max(ans,t[i])+b[c[i]];cout<<ans<<endl;//答案	}return 0;
}

学习地址：

https://www.cnblogs.com/cax1165/p/6070951.html

自行设计的通关算法：

#include<bits/stdc++.h>
using namespace std;
struct A {int min;//a,b中较小的那个int key;//记录下标
};
inline int cmp(A a,A b){return a.min<b.min;
}
int main() {int n;while(cin>>n){int* a = new int[n + 1]();//在A中的加工时间int* b = new int[n + 1]();//在B中加工的时间int* ta = new int[n + 1]();//在A中加工到第i个物品的总时间int* ans = new int[n + 1]();//存放最终加工顺序的下标 A* c = new A[n + 1];for (int i = 1; i <= n; i++) {scanf("%d",&a[i]);}for(int i=1;i<=n;i++){scanf("%d",&b[i]);c[i].min=min(a[i],b[i]);c[i].key=i;}sort(c+1,c+n+1,cmp);int u=1,v=n;//u从头开始，v从末尾开始 for(int i=1;i<=n;i++){if(c[i].min==a[c[i].key]){//如果小的数是a中的，放前面 ans[u]=c[i].key;u++;}else{//如果小的数是b中的，放后面 ans[v]=c[i].key;v--;}}for(int i=1;i<=n;i++){ta[i]=ta[i-1]+a[ans[i]];//计算ta }int sum=ta[1]+b[ans[1]];for(int i=2;i<=n;i++){sum=max(ta[i],sum)+b[ans[i]];}cout<<sum<<endl;}return 0;
}

 贪心算法之流水作业调度问题

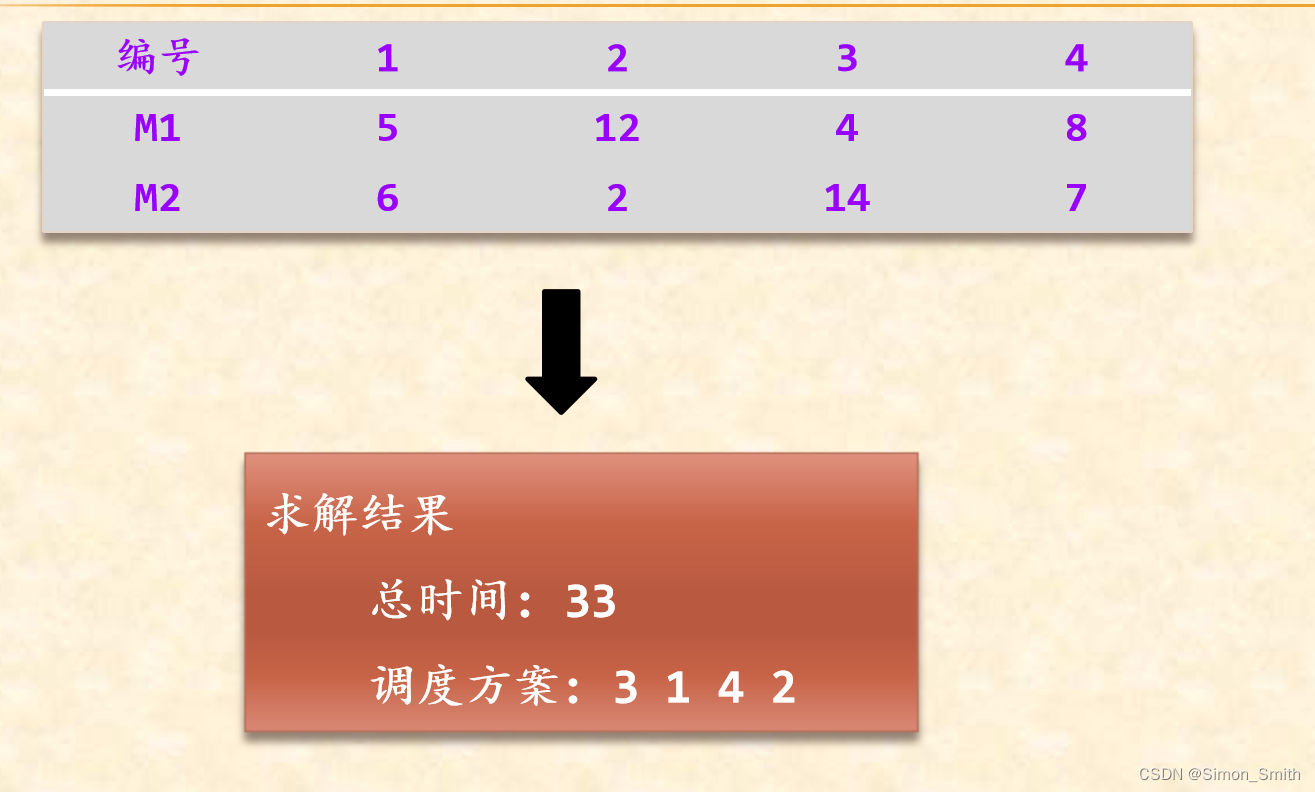
有4个作业（编号为1～4）要在由两台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi（1≤i≤n）。请给出耗时最少的最优调度方案

编号 

1

2

3

4

M1

5

12

4

8

M2

6

2

14

7

流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。可以假定任何作业一旦开始加工，就不允许被中断，直到该作业被完成。

[实验提示]

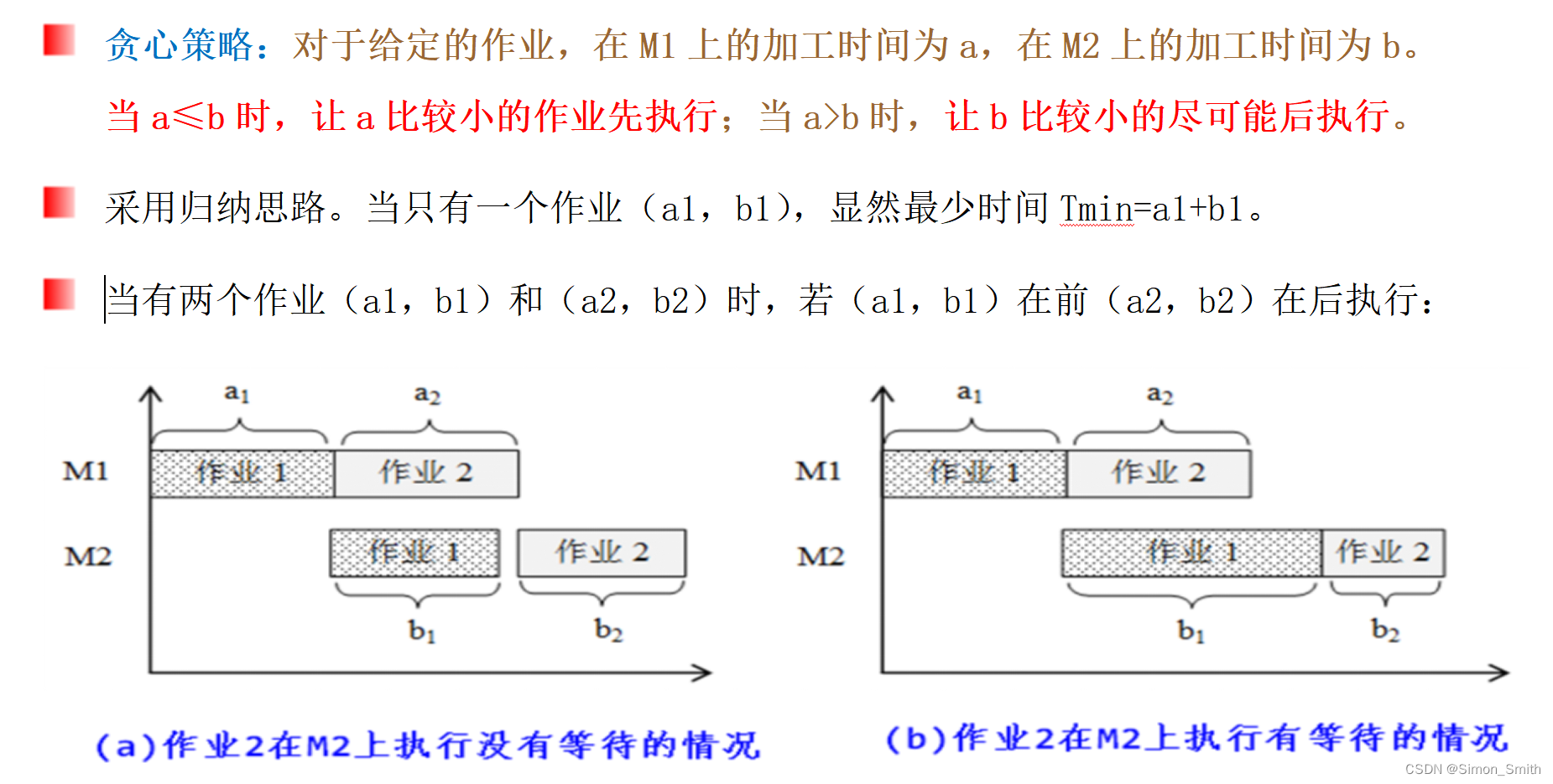
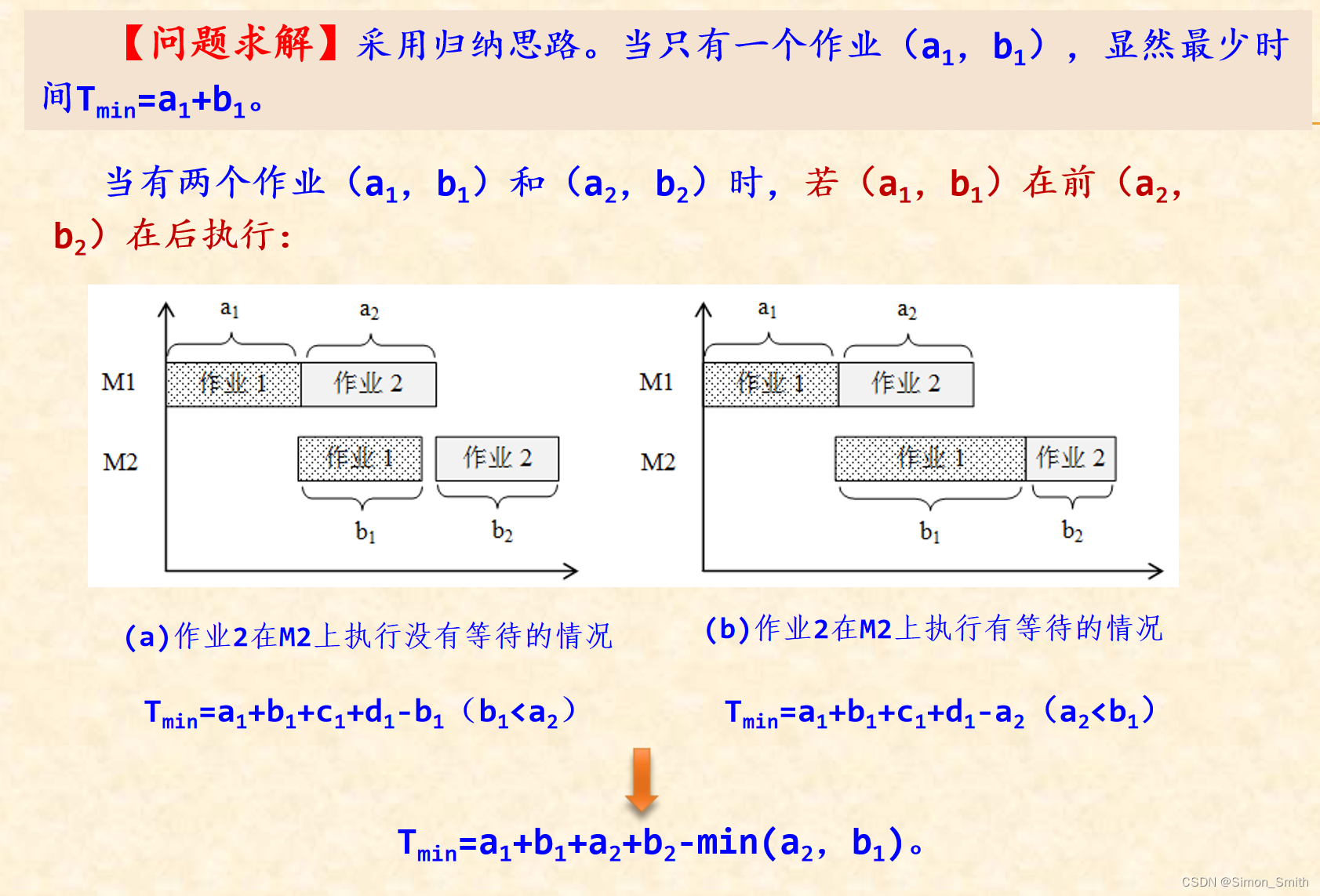
具体做法是：

组号

1

0

1

0

时间time

5

2

4

7

（2）将N1（组号=1， a[i]≤b[i] ）的作业按a[i]（用时间time存放）递增排序，N2 （组号=0， a[i]>b[i] ）的作业按b[i] （用时间time存放）递增排序。数。

编号 

1

2

3

4

M1

5

12

4

8

M2

6

2

14

7

组号

1

0

1

0

时间time

5

2

4

7

编号 

2

3

1

4

M1

12

4

5

8

M2

2

14

6

7

组号

0

1

1

0

时间time

2

4

5

7

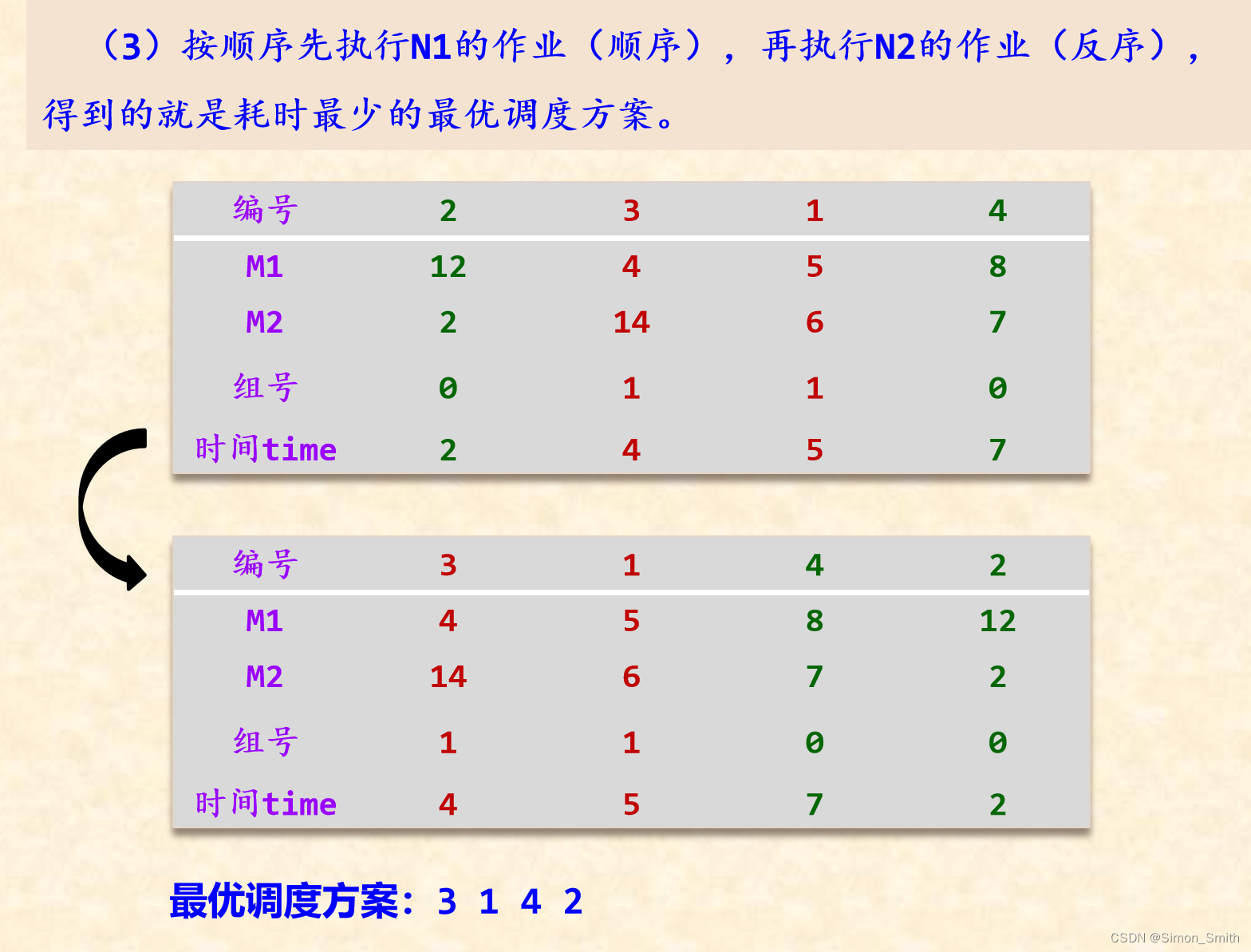
（3）按顺序先执行N1的作业（顺序），再执行N2的作业（反序），得到的就是耗时最少的最优调度方案。

编号 

2

3

1

4

M1

12

4

5

8

M2

2

14

6

7

组号

0

1

1

0

时间time

2

4

5

7

编号 

3

1

4

2

M1

4

5

8

12

M2

14

6

7

2

组号

1

1

0

0

时间time

4

5

7

2

最优调度方案：3 1 4 2

    

 [实验步骤]

1求在最优调度下总时间，用f1累计M1上的执行时间（初始时f1=0）；f2累计M2上的执行时间（初始时f2=0），最终f2即为最优调度下的消耗总时间。 

    对于最优调度方案best，用i扫描best的元素，f1和f2的计算如下：

       f1=f1+a[best[i]]

       f2=max{f1，f2}+b[best[i]]；

2针对问题实例，实录运行时的输入、输出文件；

3将你的程序和截屏的界面存盘备用。

[算法框架]

int solve() //求解流水作业调度问题

{  int i,j,k;

   NodeType c[N];

   for(i=0;i<n;i++) //n个作业中,求出每个作业的最小加工时间 

   {  c[i].no=i;

      c[i].group=(a[i]<=b[i]);

//a[i]<=b[i]对应第1组N1,a[i]>b[i]对应第0组N2

      c[i].time=a[i]<=b[i]?a[i]:b[i];

//第1组存放a[i],第0组存放b[i]

   }

   sort(c,c+n); //c元素按time递增排序

j=0; k=n-1;

   for(i=0;i<n;i++) //扫描c所有元素,产生最优调度方案

   {  if(c[i].group==1) //第1组,按time递增排列放在best的前面部分

         best[j++]=c[i].no;

      else //第0组,按time递减排列放到best的后面部分

         best[k--]=c[i].no;

   }

   int f1=0; //累计M1上的执行时间

   int f2=0; //最优调度下的消耗总时间

   for(i=0;i<n;i++)

   {  f1+=a[best[i]];

      f2=max(f2,f1)+b[best[i]];

   }

   return f2;

}

 [算法分析]

算法的主要时间花费在排序上，所以时间复杂度为O(nlog2n)。

具体的算法代码实现部分：

#include<bits/stdc++.h>
using namespace std;
struct NodeType{int no;bool group;int time;bool operator<(const NodeType &s) const{return time<s.time;}
};
int main(){int n;cout<<"please input the number of work:";cin>>n;int a[n],b[n];cout<<"please input the time of M1 and M2:";for(int i=0;i<n;i++) cin>>a[i]; cout<<"M2:"<<endl;for(int i=0;i<n;i++) cin>>b[i];int best[n];int j=0,k=n-1;NodeType c[n];for(int i=0;i<n;i++){c[i].no=i;c[i].group=(a[i]<=b[i]);c[i].time=a[i]<=b[i]?a[i]:b[i];}sort(c,c+n);for(int i=0;i<n;i++) if(c[i].group==1) best[j++]=c[i].no; else best[k--]=c[i].no;int f1=0,f2=0;for(int i=0;i<n;i++){f1+=a[best[i]];f2=max(f2,f1)+b[best[i]];}cout<<"total time:"<<f2<<endl;cout<<"plan:";for(int i=0;i<n;i++) cout<<best[i]+1;return 0;
}

 （PS：图中部分字母存在错误 自行修正即可）

 

 

struct NodeType
{  int no;			//作业序号bool group;			//1代表第一组N1,0代表第二组N2int time;			//a,b的最小时间bool operator<(const NodeType &s) const{return time<s.time;	//用于按time递增排序}
};

//问题表示
int n=4;
int a[N]={5,12,4,8};		//对应M1的时间
int b[N]={6,2,14,7};		//对应M2的时间
struct NodeType
{  int no;			//作业序号bool group;			//1代表第一组N1,0代表第二组N2int time;			//a,b的最小时间bool operator<(const NodeType &s) const{return time<s.time;	//按time递增排序}
};
//求解结果表示
int best[N];			//最优调度序列
int solve()		//求解流水作业调度问题
{  int i,j,k;NodeType c[N];for(i=0;i<n;i++)	//n个作业中,求出每个作业的最小加工时间 {  c[i].no=i;c[i].group=(a[i]<=b[i]);//a[i]<=b[i]对应第1组N1,a[i]>b[i]对应第0组N2c[i].time=a[i]<=b[i]?a[i]:b[i];//第1组存放a[i],第0组存放b[i]}sort(c,c+n);	//c元素按time递增排序j=0; k=n-1;for(i=0;i<n;i++)		//扫描c所有元素,产生最优调度方案{  if(c[i].group==1)	//第1组,按time递增排列放在best的前面部分best[j++]=c[i].no;else			//第0组,按time递减排列放到best的后面部分best[k--]=c[i].no;}int f1=0;			//累计M1上的执行时间int f2=0;			//最优调度下的消耗总时间for(i=0;i<n;i++){  f1+=a[best[i]];f2=max(f2,f1)+b[best[i]];}return f2;
}
void main()
{  printf("求解结果\n");printf("    总时间: %d\n",solve());printf("    调度方案: ");for(int i=0;i<n;i++)printf("%d ",best[i]+1);printf("\n");
}

 

 

 


http://chatgpt.dhexx.cn/article/rmAKbcai.shtml

相关文章

小程序生成网址链接，网址链接跳转小程序（附详细流程）

小程序生成网址链接，网址链接跳转小程序（附详细流程）

1.点击右上角工具下拉选择生成URL Scheme 2.填写好信息点击生成 3. 可以得出一个 weixin://dl/business/?tbAXXXXX 这样的链接&#xff0c;点击就可以调整到小程序拉&#xff0c;但是这种只能在微信打开哦。
阅读更多...
小程序接入流量主、banner广告、激励广告

小程序接入流量主、banner广告、激励广告

小程序接入广告 1.什么是微信小程序广告2.流量主开通流程3.微信小程序流量主开通以及添加广告步骤(1) 接入banner广告(2) 接入激励广告 1.什么是微信小程序广告 2.流量主开通流程 申请成为流量主后才能接入广告首先进入小程序后台&#xff0c;点击流量主&#xff0c;点击开通…
阅读更多...
微信小程序实现登录注册页面

微信小程序实现登录注册页面

一、在小程序中引入iconfont 1.在官网搜索需要的图标 2.将图标添加至项目 3.打开我的项目 4.选择font class&#xff0c;点击下方的链接&#xff0c;打开生成的源码 5.在styles文件夹下新建iconfont.wxss&#xff0c;拷贝生成的源码到该文件中 二、编写登录注册页面 …
阅读更多...
小程序获取用户的openid（详解）

小程序获取用户的openid（详解）

小程序可以通过微信官方提供的登录能力方便地获取微信提供的用户身份标识&#xff0c;快速建立小程序内的用户体系然而因为小程序中的openid不可以直接使用需要用code&#xff08;登录凭证&#xff09;去换取openid 获取openid的思路 获取openid首先需要调用小程序的login方法…
阅读更多...
微信小程序使用腾讯地图完整流程

微信小程序使用腾讯地图完整流程

前言&#xff1a;开发小程序需要得到定位和位置的省市区文字信息&#xff0c;看了所有的文章都没有一个完整和像样的&#xff0c;全是copy来&#xff0c;copy去的文章 - _ -&#xff01;&#xff0c;一怒之下&#xff0c;开始了自己的踩坑之路 第一步&#xff1a;申请腾讯地图…
阅读更多...
小程序生命周期

小程序生命周期

小程序的生命周期说白了就是指程序从创建、到开始、暂停、唤起、停止、卸载的过程。 我们大概从三个角度看一下小程序的生命周期。 &#xff08;1&#xff09;&#xff1a;应用生命周期 &#xff08;2&#xff09;&#xff1a;页面生命周期 &#xff08;3&#xff09;&…
阅读更多...
如何注册微信小程序

如何注册微信小程序

1、浏览器搜索&#xff1a; 微信公众平台 2、点击小程序 3、滑至底部&#xff0c;前往注册 4、按照注册流程依次填写信息 5、注册好后&#xff0c;来到微信公众平台&#xff0c;用微信扫码登录小程序 6、完成小程序信息的填写 7、找到开发者工具 8、前往下载开发工具 选择稳定…
阅读更多...
简述微信小程序原理

简述微信小程序原理

一、本质 首先&#xff0c;小程序的逻辑层和渲染层是分开的&#xff0c;逻辑层运行在 JSCore 中&#xff0c;并没有一个完整浏览器对象。 所以就没有相关的DOM API和BOM API&#xff0c;这一区别导致了前端开发非常熟悉的一些库&#xff0c;例如 jQuery、 Zepto 等&#xff0c…
阅读更多...
微信小程序--点餐系统（本地服务器+源码分享）

微信小程序--点餐系统（本地服务器+源码分享）

案例说明 案例来源于《微信小程序开发实战》黑马程序员著相比于原案例略有修改&#xff0c;代码也不全一样&#xff0c;有些地方的呈现效果体验更好&#xff0c;本人是看着效果图进行复现和练习的&#xff0c;最终达到了一样的效果。复现的过程中注重知识的练习&#xff0c;在…
阅读更多...
微信小程序实现收藏功能

微信小程序实现收藏功能

微信小程序收藏 前言 这篇文章主要介绍了微信小程序收藏功能的实现代码,基本功能是点击收藏后显示已收藏&#xff0c;在另一个页面出现目前点击收藏的项目。需要的朋友可以参考下。 1.首先在wxml文件中添加点击事件// 收藏 <view bindtap"haveSave"><image …
阅读更多...
如何下载小程序图片？

如何下载小程序图片？

如何下载小程序图片&#xff1f; 我们平时下载网页中的图片一般操作都是F12调试&#xff0c;或者用一些脚本插件一键下载&#xff0c;作为开发人员&#xff0c;平常用的比较多的就是Fiddler了&#xff0c;当然也用过其他的抓包工具。 但是如果要抓取小程序的图片&#xff0c;又…
阅读更多...
微信小程序部署

微信小程序部署

1. 配置服务器域名 小程序要求程序中使用到所有外部链接(HTTPS)必须将域名提前配置到微信平台。 2. 小程序api路径替换 3. 上传小程序代码 如果想让小程序被所有人在微信中使用&#xff0c;需要将小程序代码进行上传&审核&#xff0c;审核通过之后才能在微信中找到该小程…
阅读更多...
微信小程序的测试方案总结

微信小程序的测试方案总结

提纲/目标 通过对微信小程序特性和测试点进行总结&#xff0c;储备测试知识&#xff0c;提高测试效率。 小程序特性介绍小程序测试工作过程监控与管理常见问题&技巧 现状分析 接触小程序的项目相对较少缺少小程序测试实战经验对小程序的特性不了解小程序测试测试沉淀较…
阅读更多...
一、微信小程序开发详解

一、微信小程序开发详解

目录 1、什么是小程序&#xff1f; 2、小程序可以干什么&#xff1f; 3、相关资料 第一个小程序 一、申请帐号 二、测试号申请 三、安装开发工具 四、你的第一个小程序 五、编译预览 六、目录结构 七、JSON 配置 八、小程序配置 app.json 九、工具配置 project.conf…
阅读更多...
小程序 跳转到腾讯文档小程序

小程序 跳转到腾讯文档小程序

1、需求 在小程序内打开腾讯文档 2、要打开的文档 先把需要跳转的文档准备好, 然后分享出去, 方便复制链接 3、获取腾讯文档小程序的AppID&#xff1a;wxd45c635d754dbf59 4、获取小程序页面链接 在你对应的小程序后台操作&#xff1a;登录小程序 在右上角 工具 -> 生成…
阅读更多...
小程序跳转公众号

小程序跳转公众号

即用即走——这个是从微信小程序上线就开始打的概念。即用即走使得小程序可以代替许多APP&#xff0c;或是做APP的整体嫁接&#xff0c;或是作为阉割版功能的承载体。 对用户使用上来说&#xff0c;确实方便&#xff0c;要用的时候打开&#xff0c;不用的时候关掉&#xff0c;…
阅读更多...
微信小程序——开篇

微信小程序——开篇

开篇 前言锻造兵器开发者账号微信开发者工具 写在最后 前言 如今微信小程序已经成为我们日常生活中不可或缺的‘介质’&#xff0c;如我们的出行、购物、餐饮、社交、娱乐等活动的小程序已经因有尽有&#xff0c;相比于去安装一个app人们自然更加倾向于在微信中去直接访问某个…
阅读更多...
WebStrom开发微信小程序

WebStrom开发微信小程序

文章目录 WebStrom配置微信小程序一、安装微信开发者工具1、安装2、新建小程序项目3、如何查看APPID4、进入小程序开发 二、WebStrom配置小程序1、选择file->settings2、配置CSS3、配置html4、代码提示插件5、配置完成 WebStrom配置微信小程序 一、安装微信开发者工具 1、…
阅读更多...
微信小程序生态4-扫普通二维码进入小程序、打开短链接进入小程序

微信小程序生态4-扫普通二维码进入小程序、打开短链接进入小程序

文章导航 微信小程序生态1-初识小程序 微信小程序生态2-创建一个微信小程序 微信小程序生态3-微信小程序登录流程设计 微信小程序生态4-扫普通二维码进入小程序、打开短链接进入小程序 微信小程序生态5-微信公众号扫码登录PC端网页 微信小程序生态6-微信公众号授权登录(适用于…
阅读更多...
C语言程序设计（上）

C语言程序设计（上）

C语言程序设计&#xff08;第二版&#xff09;知识点总结 一、简单C程序设计变量整数类型格式化输出格式化输入浮点类型浮点数据的输出浮点数据的输入常量类型转换 二、分支结构if...else语句条件表达式常见运算符优先级switch语句 三、循环结构break语句continue语句goto语句多…
阅读更多...
推荐文章

Copyright @ 2022~2023