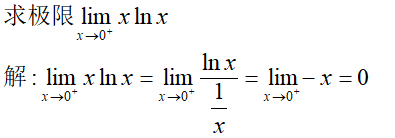1.L'Hospital法则利用柯西中值定理证明

2.该法则适用f与g同时为无穷小量或g为无穷大量的情况

3.注意该法则只给出了充分不必要条件

今天我们介绍一种函数求极限的方法——L'Hospital法则。它主要用在求解"待定型"极限

1

首先阐述定理:

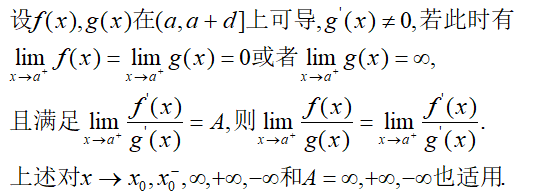
我们证明这个定理:

微分中值定理的条件是闭区间连续，开区间可导，所以第一点证明构造了端点处连续；第二点证明运用了ε-δ语言。

对于L'Hospital法则，需要注意三点。第一点我们要明确该定理的目的是为了求极限：

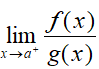
第二点是定理可用的场景是f(x)与g(x)均为无穷小量或g(x)为无穷大量：

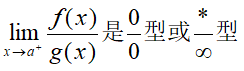
比如下面的例子不能运用该法则：

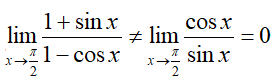
正确解法是直接运用函数极限的四则运算:

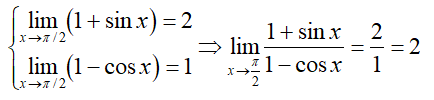
第三点是注意该定理的充分条件：

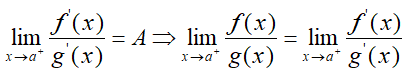
如果充分条件不满足，我们没有下面的结论:

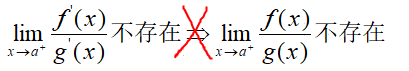
举个例子：

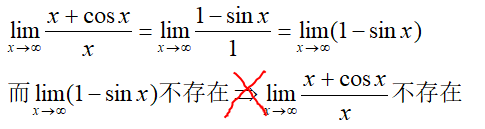
定理只给出了充分不必要条件，因此上面做法是错误的，正确解法是：

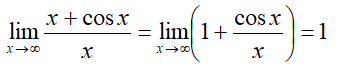
1/x是无穷小量,三角函数是有界量,无穷小量乘以有界量依然是无穷小量，再运用四则运算即可。

2

我们举一些例子来理解L'Hospital法则。

• 例1
  

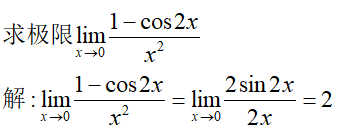
• 例2

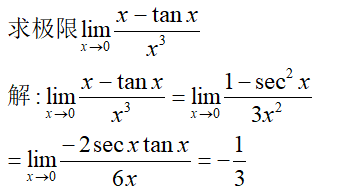
• 例3

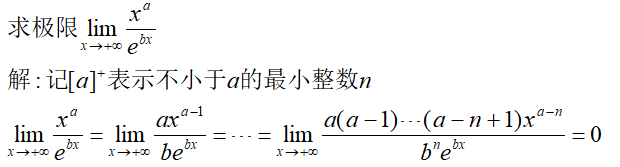
• 例4