1 Anomaly detection(异常检测)
我们的第一个任务是使用高斯模型来检测数据集中未标记的示例是否应被视为异常。 我们先从简单的二维数据集开始。
之前我们构建的异常检测系统也使用了带标记的数据,与监督学习有些相似,下面的对比有助于选择采用监督学习还是异常检测:
两者比较:
| 异常检测 | 监督学习 |
|---|---|
| 非常少量的正向类(异常数据 y = 1 y=1 y=1), 大量的负向类( y = 0 y=0 y=0) | 同时有大量的正向类和负向类 |
| 许多不同种类的异常,非常难。根据非常 少量的正向类数据来训练算法。 | 有足够多的正向类实例,足够用于训练 算法,未来遇到的正向类实例可能与训练集中的非常近似。 |
| 未来遇到的异常可能与已掌握的异常、非常的不同。 | |
| 例如: 欺诈行为检测 生产(例如飞机引擎)检测数据中心的计算机运行状况 | 例如:邮件过滤器 天气预报 肿瘤分类 |
数据可视化
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
In [3]:
data = loadmat('/home/kesci/input/andrew_ml_ex85033/ex8data1.mat')
X = data['X']
X.shape
Out[3]:
(307, 2)
In [4]:
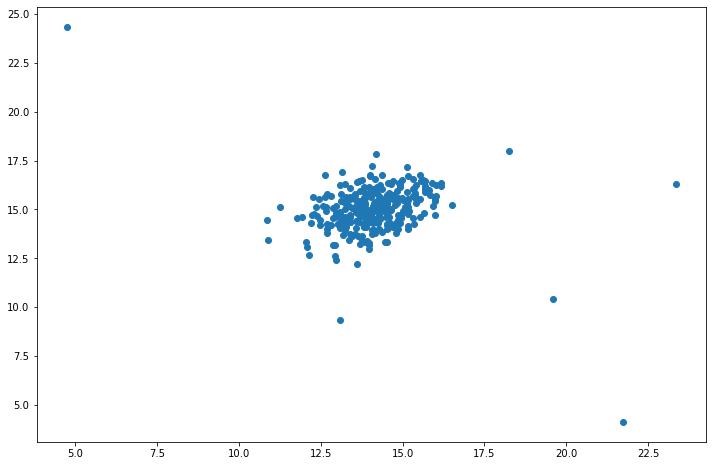
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:,0], X[:,1])
plt.show()
1.1 高斯分布
我们需要为每个特征 x i x_i xi拟合一个高斯分布,并返回高斯分布的参数 μ i , σ i 2 \mu_i,\sigma_i^2 μi,σi2。高斯分布公式如下:
p ( x ; μ , σ 2 ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} p(x;μ,σ2)=2πσ21e−2σ2(x−μ)2
其中, μ \mu μ是平均值, σ 2 \sigma^2 σ2是方差
1.2 计算高斯分布参数
μ i = 1 m ∑ j = 1 m x i ( j ) \mu_i=\frac{1}{m}\sum_{j=1}^mx_i^{(j)} μi=m1j=1∑mxi(j)
σ i 2 = 1 m ∑ j = 1 m ( x i ( j ) − μ i ) 2 \sigma_i^2=\frac{1}{m}\sum_{j=1}^m(x_i^{(j)}-\mu_i)^2 σi2=m1j=1∑m(xi(j)−μi)2
你要做的是,输入一个X矩阵,输出2个n维的向量, μ \mu μ包含了每一个维度的平均值, σ 2 \sigma^2 σ2包含了每一个维度的方差。
In [5]:
def estimate_gaussian(X):mu = X.mean(axis=0)sigma = X.var(axis=0)return mu, sigma
In [6]:
mu, sigma = estimate_gaussian(X)
mu, sigma
Out[6]:
(array([14.11222578, 14.99771051]), array([1.83263141, 1.70974533]))
数据可视化
In [7]:
xplot = np.linspace(0, 25, 100)
yplot = np.linspace(0, 25, 100)
Xplot, Yplot = np.meshgrid(xplot, yplot)
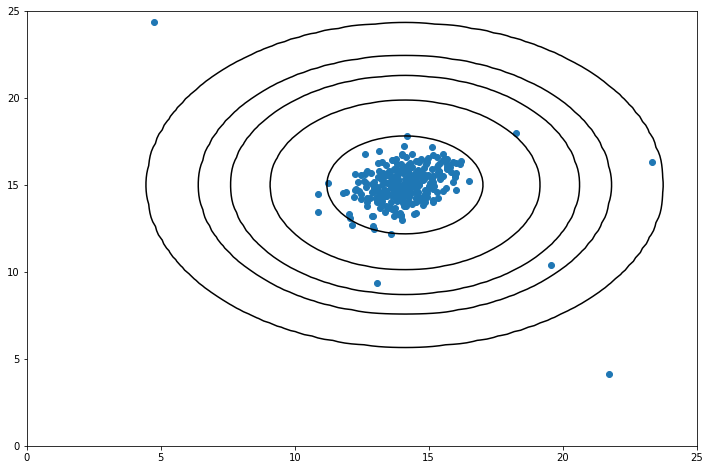
Z = np.exp((-0.5) * ((Xplot - mu[0]) ** 2 / sigma[0] + (Yplot - mu[1]) ** 2 / sigma[1])) # 概率之积fig, ax = plt.subplots(figsize=(12, 8))
contour = plt.contour(Xplot, Yplot, Z, [10 ** -11, 10 ** -7, 10 ** -5, 10 ** -3, 0.1], colors='k')
ax.scatter(X[:, 0], X[:, 1])
plt.show()
'''
plt.contour(X, Y, Z, [levels], **kwargs)plt就是matplotlib.pyplot
X, Y表示的是坐标位置(这里是可选的,但是如果不传入的话就是python根据传入的高度数组(Z)的大小自动生成的坐标),一般很多会使用二维数组,但是实际上一维数组也可以的
Z代表每个坐标对应的高度值,是一个二维数组,其中每个值表示的是每个坐标对应的高度 XYZ的实际数据构成可以参照上面的例子,在本地查看一下数据是长什么样
levels有两种传入形式。一种是传入一个整数,这个整数表示你想绘制的等高线的条数,但是显示结果可能并不是完全和传入的整数的条数一样,是大致差不多的条数(可能相差一两条)(为什么是大致条数呢?可能是python帮你默认生成的比较合适的几条等高线吧)。还有一种方式就是传入一个包含高度值的一维数组,这样python便会画出传入的高度值对应的等高线。
其余的参数cmap, linewidths, linestyles等这里就不多介绍了
'''
1.3 选择阈值ε
有了参数后,可以估计每组数据的概率,低概率的数据点更可能是异常的。确定异常点需要先确定一个阈值,我们可以通过验证集集来确定这个阈值。
In [8]:
Xval = data['Xval']
yval = data['yval']Xval.shape, yval.shape
Out[8]:
((307, 2), (307, 1))
我们还需要一种计算数据点属于正态分布的概率的方法。 幸运的是SciPy有这个内置的方法。
In [9]:
from scipy import stats
dist = stats.norm(mu[0], np.sqrt(sigma[0])) # 概率密度函数
dist.pdf(15)
'''
norm.pdf(x, loc, scale)等同于norm.pdf(y) / scale ,其中 y = (x - loc) / scale
loc: mean 均值, scale: standard deviation 标准差
stats.norm主要公共方法如下:
rvs:随机变量(就是从这个分布中抽一些样本)
pdf:概率密度函数。
cdf:累计分布函数
sf:残存函数(1-CDF)
ppf:分位点函数(CDF的逆)
isf:逆残存函数(sf的逆)
stats:返回均值,方差,(费舍尔)偏态,(费舍尔)峰度。
moment:分布的非中心矩。'''
Out[9]:
0.23767635105892454
我们还可以将数组传递给概率密度函数,并获得数据集中每个点的概率密度。
In [10]:
dist.pdf(X[:,0])[0:50]
Out[10]:
array([0.21620977, 0.25745208, 0.29413223, 0.24721192, 0.27251547,0.2918119 , 0.18713958, 0.15117648, 0.09356331, 0.166609 ,0.29338708, 0.29448769, 0.25559237, 0.25595621, 0.2932714 ,0.2944456 , 0.29288017, 0.28518331, 0.27727759, 0.09489765,0.27027271, 0.29342161, 0.24110555, 0.29304288, 0.19607729,0.15652979, 0.27590459, 0.25749622, 0.27667047, 0.2834953 ,0.17068283, 0.29318613, 0.20432637, 0.19577297, 0.10897052,0.24595126, 0.14063746, 0.29463374, 0.28052751, 0.29371857,0.28168158, 0.22524293, 0.28218942, 0.29429662, 0.26674962,0.28856013, 0.11137104, 0.29467721, 0.28904196, 0.18556585])
我们计算并保存给定上述的高斯模型参数的数据集中每个值的概率密度。
In [11]:
p = np.zeros((X.shape[0], X.shape[1]))
p[:,0] = stats.norm(mu[0], np.sqrt(sigma[0])).pdf(X[:,0])
p[:,1] = stats.norm(mu[1], np.sqrt(sigma[1])).pdf(X[:,1])p.shape
Out[11]:
(307, 2)
我们还需要为验证集(使用相同的模型参数)执行此操作。 我们将使用与真实标签组合的这些概率来确定将数据点分配为异常的最佳概率阈值。
In [12]:
pval = np.zeros((Xval.shape[0], Xval.shape[1]))
pval[:,0] = stats.norm(mu[0], np.sqrt(sigma[0])).pdf(Xval[:,0])
pval[:,1] = stats.norm(mu[1], np.sqrt(sigma[1])).pdf(Xval[:,1])pval.shape
Out[12]:
(307, 2)
接下来,我们需要一个函数,找到给定概率密度值和真实标签的最佳阈值。 为了做到这一点,我们将为不同的epsilon值计算F1分数。 F1是真阳性,假阳性和假阴性的数量的函数。 方程式在练习文本中。
'''
np.arange()
np.arange()函数返回一个有终点和起点的固定步长的排列,如[1,2,3,4,5],起点是1,终点是6,步长为1。
参数个数情况: np.arange()函数分为一个参数,两个参数,三个参数三种情况
一个参数时,参数值为终点,起点取默认值0,步长取默认值1。
两个参数时,第一个参数为起点,第二个参数为终点,步长取默认值1。
三个参数时,第一个参数为起点,第二个参数为终点,第三个参数为步长。其中步长支持小数range()
函数语法:
range(stop)
range(start, stop[, step])
参数说明:
start: 计数从 start 开始。默认是从 0 开始。例如range(5)等价于range(0, 5);
stop: 计数到 stop 结束,但不包括 stop。例如:range(0, 5) 是[0, 1, 2, 3, 4]没有5
step:步长,默认为1。例如:range(0, 5) 等价于 range(0, 5, 1)注意range()和np.arange()区别
arange()是Numpy中的函数,它和python自带函数range()的功能貌似比较相同。但是range()和np.arange()有一些区别:
range()和np.arange()的返回类型不同,range()返回的是range这个object,而np.arange()返回的是ndarray类型;
range()不支持步长为小数,而np.arange()支持步长(step)为小数;
range()和np.arange()都可用于迭代;
range()和np.arange()都有三个参数,以第一个参数为起点,第三个参数为步长,截止到第二个参数之前的不包括第二个参数的数据序列。
range()可用于迭代,而np.arange()作用远不止于此,它是一个序列,可被当做向量使用。
'''
In [13]:
def select_threshold(pval, yval):best_epsilon = 0best_f1 = 0f1 = 0step = (pval.max() - pval.min()) / 1000for epsilon in np.arange(pval.min(), pval.max(), step):preds = pval < epsilontp = np.sum(np.logical_and(preds == 1, yval == 1)).astype(float)fp = np.sum(np.logical_and(preds == 1, yval == 0)).astype(float)fn = np.sum(np.logical_and(preds == 0, yval == 1)).astype(float)precision = tp / (tp + fp)recall = tp / (tp + fn)f1 = (2 * precision * recall) / (precision + recall)if f1 > best_f1:best_f1 = f1best_epsilon = epsilonreturn best_epsilon, best_f1
In [14]:
epsilon, f1 = select_threshold(pval, yval)
epsilon, f1
/opt/conda/lib/python3.7/site-packages/ipykernel_launcher.py:15: RuntimeWarning: invalid value encountered in double_scalarsfrom ipykernel import kernelapp as app
Out[14]:
(0.0015255071244515167, 0.7142857142857143)
最后,我们可以将阈值应用于数据集,并可视化结果。
In [15]:
# indexes of the values considered to be outliers
outliers = np.where(p < epsilon)
outliers
Out[15]:
(array([300, 301, 301, 303, 303, 304, 306, 306]),array([1, 0, 1, 0, 1, 0, 0, 1]))
In [16]:
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(X[:, 0], X[:, 1])
ax.scatter(X[outliers[0], 0], X[outliers[0], 1], s=50, color='r', marker='o')
plt.show()
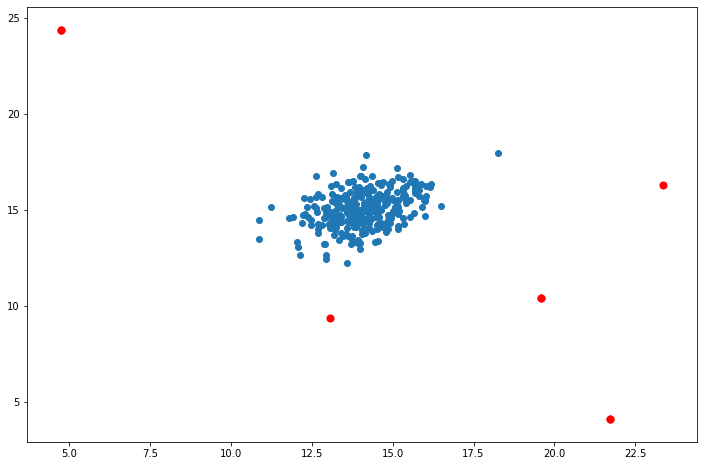
红点是被标记为异常值的点。 这些看起来很合理。 有一些分离(但没有被标记)的右上角也可能是一个异常值,但是相当接近。
1.4 高斯多元分布
在一般的高斯分布模型中,我们计算 p ( x ) p(x) p(x) 的方法是:
通过分别计算每个特征对应的几率然后将其累乘起来,在多元高斯分布模型中,我们将构建特征的协方差矩阵,用所有的特征一起来计算 p ( x ) p(x) p(x)。
我们首先计算所有特征的平均值,然后再计算协方差矩阵:
p ( x ) = ∏ j = 1 n p ( x j ; μ , σ j 2 ) = ∏ j = 1 n 1 2 π σ j e x p ( − ( x j − μ j ) 2 2 σ j 2 ) p(x)=\prod_{j=1}^np(x_j;\mu,\sigma_j^2)=\prod_{j=1}^n\frac{1}{\sqrt{2\pi}\sigma_j}exp(-\frac{(x_j-\mu_j)^2}{2\sigma_j^2}) p(x)=j=1∏np(xj;μ,σj2)=j=1∏n2πσj1exp(−2σj2(xj−μj)2)
μ = 1 m ∑ i = 1 m x ( i ) \mu=\frac{1}{m}\sum_{i=1}^mx^{(i)} μ=m1i=1∑mx(i)
Σ = 1 m ∑ i = 1 m ( x ( i ) − μ ) ( x ( i ) − μ ) T = 1 m ( X − μ ) T ( X − μ ) \Sigma = \frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T=\frac{1}{m}(X-\mu)^T(X-\mu) Σ=m1i=1∑m(x(i)−μ)(x(i)−μ)T=m1(X−μ)T(X−μ)
注:其中$\mu $ 是一个向量,其每一个单元都是原特征矩阵中一行数据的均值。最后我们计算多元高斯分布的 p ( x ) p\left( x \right) p(x):
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x)=\frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right) p(x)=(2π)2n∣Σ∣211exp(−21(x−μ)TΣ−1(x−μ))
其中:
∣ Σ ∣ |\Sigma| ∣Σ∣是定矩阵,在 Octave 中用 det(sigma)计算
Σ − 1 \Sigma^{-1} Σ−1 是逆矩阵,下面我们来看看协方差矩阵是如何影响模型的:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-smbdRPwF-1658243739275)(C:\Users\myp\AppData\Roaming\Typora\typora-user-images\image-20220718145036680.png)]](https://img-blog.csdnimg.cn/31e6cafa2d604cd18b9f2d035be06ed1.png)
上图是5个不同的模型,从左往右依次分析:
-
是一个一般的高斯分布模型
-
通过协方差矩阵,令特征1拥有较小的偏差,同时保持特征2的偏差
-
通过协方差矩阵,令特征2拥有较大的偏差,同时保持特征1的偏差
-
通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的正相关性
-
通过协方差矩阵,在不改变两个特征的原有偏差的基础上,增加两者之间的负相关性
多元高斯分布模型与原高斯分布模型的关系:
可以证明的是,原本的高斯分布模型是多元高斯分布模型的一个子集,即像上图中的第1、2、3,3个例子所示,如果协方差矩阵只在对角线的单位上有非零的值时,即为原本的高斯分布模型了。
原高斯分布模型和多元高斯分布模型的比较:
| 原高斯分布模型 | 多元高斯分布模型 |
|---|---|
| 不能捕捉特征之间的相关性 但可以通过将特征进行组合的方法来解决 | 自动捕捉特征之间的相关性 |
| 计算代价低,能适应大规模的特征 | 计算代价较高 训练集较小时也同样适用 |
| 必须要有 m > n m>n m>n,不然的话协方差矩阵 Σ \Sigma Σ不可逆的,通常需要 m > 10 n m>10n m>10n 另外特征冗余也会导致协方差矩阵不可逆 |
原高斯分布模型被广泛使用着,如果特征之间在某种程度上存在相互关联的情况,我们可以通过构造新新特征的方法来捕捉这些相关性。
如果训练集不是太大,并且没有太多的特征,我们可以使用多元高斯分布模型。
2 推荐系统
每部电影都有一个特征向量,如 x ( 1 ) x^{(1)} x(1)是第一部电影的特征向量为[0.9 0]。
下面我们要基于这些特征来构建一个推荐系统算法。
假设我们采用线性回归模型,我们可以针对每一个用户都训练一个线性回归模型,如 θ ( 1 ) {{\theta }^{(1)}} θ(1)是第一个用户的模型的参数。
于是,我们有:
θ ( j ) \theta^{(j)} θ(j)用户 j j j 的参数向量
x ( i ) x^{(i)} x(i)电影 i i i 的特征向量
对于用户 j j j 和电影 i i i,我们预测评分为: ( θ ( j ) ) T x ( i ) (\theta^{(j)})^T x^{(i)} (θ(j))Tx(i)
代价函数
针对用户 j j j,该线性回归模型的代价为预测误差的平方和,加上正则化项:
min θ ( j ) 1 2 ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ( θ k ( j ) ) 2 \min_{\theta (j)}\frac{1}{2}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\left(\theta_{k}^{(j)}\right)^2 θ(j)min21i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λ(θk(j))2
其中 i : r ( i , j ) i:r(i,j) i:r(i,j)表示我们只计算那些用户 j j j 评过分的电影。在一般的线性回归模型中,误差项和正则项应该都是乘以 1 / 2 m 1/2m 1/2m,在这里我们将 m m m去掉。并且我们不对方差项 θ 0 \theta_0 θ0进行正则化处理。
上面的代价函数只是针对一个用户的,为了学习所有用户,我们将所有用户的代价函数求和:
min θ ( 1 ) , . . . , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 \min_{\theta^{(1)},...,\theta^{(n_u)}} \frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}\left((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\right)^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 θ(1),...,θ(nu)min21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
如果我们要用梯度下降法来求解最优解,我们计算代价函数的偏导数后得到梯度下降的更新公式为:
θ k ( j ) : = θ k ( j ) − α ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) ( for k = 0 ) \theta_k^{(j)}:=\theta_k^{(j)}-\alpha\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)} \quad (\text{for} \, k = 0) θk(j):=θk(j)−αi:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)(fork=0)
θ k ( j ) : = θ k ( j ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) x k ( i ) + λ θ k ( j ) ) ( for k ≠ 0 ) \theta_k^{(j)}:=\theta_k^{(j)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})x_{k}^{(i)}+\lambda\theta_k^{(j)}\right) \quad (\text{for} \, k\neq 0) θk(j):=θk(j)−α⎝ ⎛i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))xk(i)+λθk(j)⎠ ⎞(fork=0)
3 协同过滤
在之前的基于内容的推荐系统中,对于每一部电影,我们都掌握了可用的特征,使用这些特征训练出了每一个用户的参数。相反地,如果我们拥有用户的参数,我们可以学习得出电影的特征。
m i n x ( 1 ) , . . . , x ( n m ) 1 2 ∑ i = 1 n m ∑ j r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 \mathop{min}\limits_{x^{(1)},...,x^{(n_m)}}\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j{r(i,j)=1}}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2 x(1),...,x(nm)min21i=1∑nmjr(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2
但是如果我们既没有用户的参数,也没有电影的特征,这两种方法都不可行了。协同过滤算法可以同时学习这两者。
我们的优化目标便改为**同时针对 x x x和 θ \theta θ**进行。
J ( x ( 1 ) , . . . x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) = 1 2 ∑ ( i : j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 J(x^{(1)},...x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i:j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 J(x(1),...x(nm),θ(1),...,θ(nu))=21(i:j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(j))2+2λj=1∑nuk=1∑n(θk(j))2
对代价函数求偏导数的结果如下:
x k ( i ) : = x k ( i ) − α ( ∑ j : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) θ k j + λ x k ( i ) ) x_k^{(i)}:=x_k^{(i)}-\alpha\left(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}\theta_k^{j}+\lambda x_k^{(i)}\right) xk(i):=xk(i)−α⎝ ⎛j:r(i,j)=1∑((θ(j))Tx(i)−y(i,j)θkj+λxk(i)⎠ ⎞
θ k ( i ) : = θ k ( i ) − α ( ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) x k ( i ) + λ θ k ( j ) ) \theta_k^{(i)}:=\theta_k^{(i)}-\alpha\left(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)}x_k^{(i)}+\lambda \theta_k^{(j)}\right) θk(i):=θk(i)−α⎝ ⎛i:r(i,j)=1∑((θ(j))Tx(i)−y(i,j)xk(i)+λθk(j)⎠ ⎞
注:在协同过滤从算法中,我们通常不使用截距项,如果需要的话,算法会自动学得。
协同过滤算法使用步骤如下:
-
初始 x ( 1 ) , x ( 1 ) , . . . x ( n m ) , θ ( 1 ) , θ ( 2 ) , . . . , θ ( n u ) x^{(1)},x^{(1)},...x^{(nm)},\ \theta^{(1)},\theta^{(2)},...,\theta^{(n_u)} x(1),x(1),...x(nm), θ(1),θ(2),...,θ(nu)为一些随机小值
-
使用梯度下降算法最小化代价函数
-
在训练完算法后,我们预测 ( θ ( j ) ) T x ( i ) (\theta^{(j)})^Tx^{(i)} (θ(j))Tx(i)为用户 j j j 给电影 i i i 的评分
通过这个学习过程获得的特征矩阵包含了有关电影的重要数据,这些数据不总是人能读懂的,但是我们可以用这些数据作为给用户推荐电影的依据。
例如,如果一位用户正在观看电影 x ( i ) x^{(i)} x(i),我们可以寻找另一部电影 x ( j ) x^{(j)} x(j),依据两部电影的特征向量之间的距离 ∥ x ( i ) − x ( j ) ∥ \left\| {{x}^{(i)}}-{{x}^{(j)}} \right\| ∥ ∥x(i)−x(j)∥ ∥的大小。
协同过滤优化目标:
给定 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm),估计 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
min θ ( 1 ) , . . . , θ ( n u ) 1 2 ∑ j = 1 n u ∑ i : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 \min_{\theta^{(1)},...,\theta^{(n_u)}}\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 θ(1),...,θ(nu)min21j=1∑nui:r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λj=1∑nuk=1∑n(θk(j))2
给定 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu),估计 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm):
m i n x ( 1 ) , . . . , x ( n m ) 1 2 ∑ i = 1 n m ∑ j r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 \mathop{min}\limits_{x^{(1)},...,x^{(n_m)}}\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j{r(i,j)=1}}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2 x(1),...,x(nm)min21i=1∑nmjr(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2
同时最小化 x ( 1 ) , . . . , x ( n m ) x^{(1)},...,x^{(n_m)} x(1),...,x(nm)和 θ ( 1 ) , . . . , θ ( n u ) \theta^{(1)},...,\theta^{(n_u)} θ(1),...,θ(nu):
J ( x ( 1 ) , . . . , x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) = 1 2 ∑ ( i , j ) : r ( i , j ) = 1 ( ( θ ( j ) ) T x ( i ) − y ( i , j ) ) 2 + λ 2 ∑ i = 1 n m ∑ k = 1 n ( x k ( i ) ) 2 + λ 2 ∑ j = 1 n u ∑ k = 1 n ( θ k ( j ) ) 2 J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})=\frac{1}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_k^{(i)})^2+\frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_k^{(j)})^2 J(x(1),...,x(nm),θ(1),...,θ(nu))=21(i,j):r(i,j)=1∑((θ(j))Tx(i)−y(i,j))2+2λi=1∑nmk=1∑n(xk(i))2+2λj=1∑nuk=1∑n(θk(j))2
min x ( 1 ) , . . . , x ( n m ) θ ( 1 ) , . . . , θ ( n u ) J ( x ( 1 ) , . . . , x ( n m ) , θ ( 1 ) , . . . , θ ( n u ) ) \min_{x^{(1)},...,x^{(n_m)} \\\ \theta^{(1)},...,\theta^{(n_u)}}J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}) x(1),...,x(nm) θ(1),...,θ(nu)minJ(x(1),...,x(nm),θ(1),...,θ(nu))
推荐引擎使用基于项目和用户的相似性度量来检查用户的历史偏好,以便为用户可能感兴趣的新“事物”提供建议。在本练习中,我们将实现一种称为协作过滤的特定推荐系统算法,并将其应用于 电影评分的数据集。
我们首先加载并检查我们将要使用的数据。
In [45]:
data = loadmat('/home/kesci/input/andrew_ml_ex85033/ex8_movies.mat')
data
Out[45]:
{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Thu Dec 1 17:19:26 2011','__version__': '1.0','__globals__': [],'Y': array([[5, 4, 0, ..., 5, 0, 0],[3, 0, 0, ..., 0, 0, 5],[4, 0, 0, ..., 0, 0, 0],...,[0, 0, 0, ..., 0, 0, 0],[0, 0, 0, ..., 0, 0, 0],[0, 0, 0, ..., 0, 0, 0]], dtype=uint8),'R': array([[1, 1, 0, ..., 1, 0, 0],[1, 0, 0, ..., 0, 0, 1],[1, 0, 0, ..., 0, 0, 0],...,[0, 0, 0, ..., 0, 0, 0],[0, 0, 0, ..., 0, 0, 0],[0, 0, 0, ..., 0, 0, 0]], dtype=uint8)}
Y是包含从1到5的等级的(数量的电影x数量的用户)数组.R是包含指示用户是否给电影评分的二进制值的“指示符”数组。 两者应该具有相同的维度。
In [46]:
Y = data['Y']
R = data['R']
Y.shape, R.shape
Out[46]:
((1682, 943), (1682, 943))
我们可以通过平均排序Y来评估电影的平均评级。
In [47]:
Y[1,np.where(R[1,:]==1)[0]].mean()
Out[47]:
3.2061068702290076
我们还可以通过将矩阵渲染成图像来尝试“可视化”数据。 我们不能从这里收集太多,但它确实给我们了解用户和电影的相对密度。
In [48]:
fig, ax = plt.subplots(figsize=(12,12))
ax.imshow(Y)
ax.set_xlabel('Users')
ax.set_ylabel('Movies')
fig.tight_layout()
plt.show()
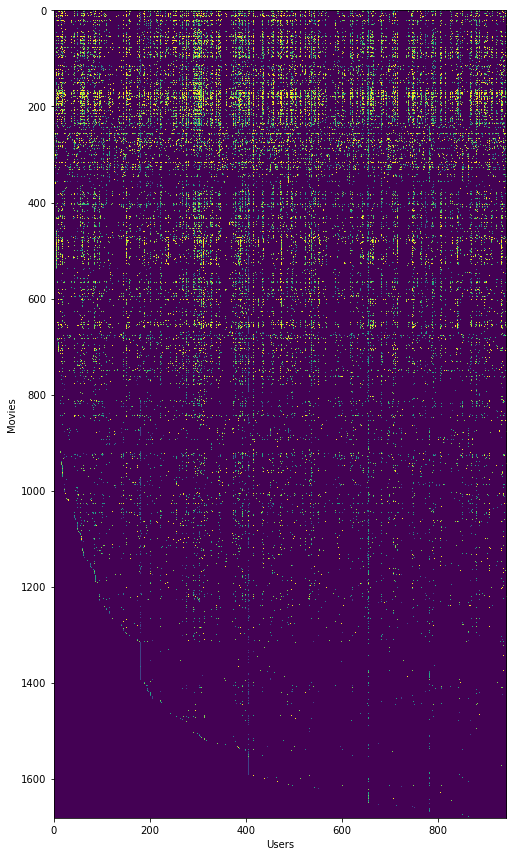
接下来,我们将实施协同过滤的代价函数。 直觉上,“代价”是指一组电影评级预测偏离真实预测的程度。 代价方程在练习文本中给出。 它基于文本中称为X和Theta的两组参数矩阵。 这些“展开”到“参数”输入中,以便稍后可以使用SciPy的优化包。 请注意,我已经在注释中包含数组/矩阵形状(对于我们在本练习中使用的数据),以帮助说明矩阵交互如何工作。
3.1 cost
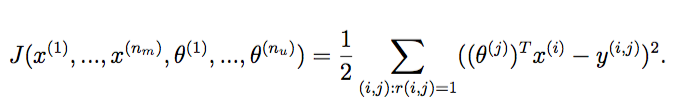
In [49]:
def serialize(X, theta):"""序列化两个矩阵"""# X (movie, feature), (1682, 10): movie features# theta (user, feature), (943, 10): user preferencereturn np.concatenate((X.ravel(), theta.ravel()))def deserialize(param, n_movie, n_user, n_features):"""逆序列化"""return param[:n_movie * n_features].reshape(n_movie, n_features), param[n_movie * n_features:].reshape(n_user, n_features)# recommendation fn
def cost(param, Y, R, n_features):"""compute cost for every r(i, j)=1Args:param: serialized X, thetaY (movie, user), (1682, 943): (movie, user) ratingR (movie, user), (1682, 943): (movie, user) has rating"""# theta (user, feature), (943, 10): user preference# X (movie, feature), (1682, 10): movie featuresn_movie, n_user = Y.shapeX, theta = deserialize(param, n_movie, n_user, n_features)inner = np.multiply(X @ theta.T - Y, R) # 评过分的预测值return np.power(inner, 2).sum() / 2
为了测试这一点,我们提供了一组我们可以评估的预训练参数。 为了保持评估时间的少点,我们将只看一小段数据。
In [50]:
params_data = loadmat('/home/kesci/input/andrew_ml_ex85033/ex8_movieParams.mat')
X = params_data['X']
theta = params_data['Theta']
X.shape, theta.shape
Out[50]:
((1682, 10), (943, 10))
In [51]:
users = 4
movies = 5
features = 3X_sub = X[:movies, :features]
theta_sub = theta[:users, :features]
Y_sub = Y[:movies, :users]
R_sub = R[:movies, :users]param_sub = serialize(X_sub, theta_sub)cost(param_sub, Y_sub, R_sub, features)
Out[51]:
22.224603725685675
In [52]:
param = serialize(X, theta) # total real paramscost(serialize(X, theta), Y, R, 10) # this is real total cost
Out[52]:
27918.64012454421
3.2 gradient
接下来我们需要实现梯度计算。 就像我们在练习4中使用神经网络实现一样,我们将扩展代价函数来计算梯度。
In [53]:
def gradient(param, Y, R, n_features):# theta (user, feature), (943, 10): user preference# X (movie, feature), (1682, 10): movie featuresn_movies, n_user = Y.shapeX, theta = deserialize(param, n_movies, n_user, n_features)inner = np.multiply(X @ theta.T - Y, R) # (1682, 943)# X_grad (1682, 10)X_grad = inner @ theta# theta_grad (943, 10)theta_grad = inner.T @ X# roll them together and returnreturn serialize(X_grad, theta_grad)
In [54]:
n_movie, n_user = Y.shapeX_grad, theta_grad = deserialize(gradient(param, Y, R, 10),n_movie, n_user, 10)
X_grad, theta_grad
Out[54]:
(array([[-6.26184144, 2.45936046, -6.87560329, ..., -4.81611896,3.84341521, -1.88786696],[-3.80931446, 1.80494255, -2.63877955, ..., -3.55580057,2.1709485 , 2.65129032],[-3.13090116, 2.54853961, 0.23884578, ..., -4.18778519,3.10538294, 5.47323609],...,[-1.04774171, 0.99220776, -0.48920899, ..., -0.75342146,0.32607323, -0.89053637],[-0.7842118 , 0.76136861, -1.25614442, ..., -1.05047808,1.63905435, -0.14891962],[-0.38792295, 1.06425941, -0.34347065, ..., -2.04912884,1.37598855, 0.19551671]]),array([[-1.54728877, 9.0812347 , -0.6421836 , ..., -3.92035321,5.66418748, 1.16465605],[-2.58829914, 2.52342335, -1.52402705, ..., -5.46793491,5.82479897, 1.8849854 ],[ 2.14588899, 2.00889578, -4.32190712, ..., -6.83365682,1.78952063, 0.82886788],...,[-4.59816821, 3.63958389, -2.52909095, ..., -3.50886008,2.99859566, 0.64932177],[-4.39652679, 0.55036362, -1.98451805, ..., -6.74723702,3.8538775 , 3.94901737],[-3.75193726, 1.44393885, -5.6925333 , ..., -6.56073746,5.20459188, 2.65003952]]))
3.3 regularized cost & regularized gradient
我们的下一步是在代价和梯度计算中添加正则化。 我们将创建一个最终的正则化版本的功能(请注意,此版本包含一个额外的“学习率”参数,在文本中称为“lambda”)。
In [55]:
def regularized_cost(param, Y, R, n_features, l=1):reg_term = np.power(param, 2).sum() * (l / 2)return cost(param, Y, R, n_features) + reg_termdef regularized_gradient(param, Y, R, n_features, l=1):grad = gradient(param, Y, R, n_features)reg_term = l * paramreturn grad + reg_term
In [56]:
regularized_cost(param_sub, Y_sub, R_sub, features, l=1.5)
Out[56]:
31.34405624427422
In [57]:
regularized_cost(param, Y, R, 10, l=1) # total regularized cost
Out[57]:
32520.682450229557
In [58]:
n_movie, n_user = Y.shapeX_grad, theta_grad = deserialize(regularized_gradient(param, Y, R, 10),n_movie, n_user, 10)
这个结果再次与练习代码的预期输出相匹配,所以看起来正则化是正常的。 在我们训练模型之前,我们有一个最后步骤, 我们的任务是创建自己的电影评分,以便我们可以使用该模型来生成个性化的推荐。 为我们提供一个连接电影索引到其标题的文件。 接着我们将文件加载到字典中。
In [59]:
movie_list = []
f = open('/home/kesci/input/andrew_ml_ex85033/movie_ids.txt',encoding= 'gbk')for line in f:tokens = line.strip().split(' ')movie_list.append(' '.join(tokens[1:]))movie_list = np.array(movie_list)
'''
strip() 方法用于移除字符串头尾指定的字符(默认为空格)。
str.strip([c])split()方法通过指定分隔符对字符串进行切片,如果参数num 有指定值,则仅分隔 num 个子字符串
str.split(str="", num=string.count(str)).'''
In [60]:
movie_list[0]
Out[60]:
'Toy Story (1995)'
我们将使用练习中提供的评分。
In [66]:
ratings = np.zeros((1682, 1))ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5ratings.shape
Out[66]:
(1682, 1)
我们可以将自己的评级向量添加到现有数据集中以包含在模型中。
In [71]:
Y = data['Y']
Y = np.append(ratings,Y, axis=1) # now I become user 0
print(Y.shape)
(1682, 944)
In [72]:
R = data['R']
R = np.append( ratings != 0, R,axis=1)
R.shape
Out[72]:
(1682, 944)
我们不只是准备训练协同过滤模型。 我们只需要定义一些变量并对评级进行规一化。
In [73]:
movies = Y.shape[0] # 1682
users = Y.shape[1] # 944
features = 10
learning_rate = 10.X = np.random.random(size=(movies, features))
theta = np.random.random(size=(users, features))
params = serialize(X, theta)X.shape, theta.shape, params.shape
Out[73]:
((1682, 10), (944, 10), (26260,))
In [74]:
Y_norm = Y - Y.mean()
Y_norm.mean()
Out[74]:
4.6862111343939375e-17
3.4 training
In [75]:
from scipy.optimize import minimizefmin = minimize(fun=regularized_cost, x0=params, args=(Y_norm, R, features, learning_rate), method='TNC', jac=regularized_gradient)
fmin
Out[75]:
fun: 69383.27505093074jac: array([ 1.22325170e-05, 1.03344221e-06, 2.14135825e-05, ...,1.11228726e-06, -4.49512066e-07, 3.21855995e-07])message: 'Converged (|f_n-f_(n-1)| ~= 0)'nfev: 1130nit: 43status: 1success: Truex: array([ 0.52681315, 0.47497643, -0.30179615, ..., 0.80610143,0.01011655, 0.43714604])
我们训练好的参数是X和Theta。 我们可以使用这些来为我们添加的用户创建一些建议。
In [76]:
X_trained, theta_trained = deserialize(fmin.x, movies, users, features)
X_trained.shape, theta_trained.shape
Out[76]:
((1682, 10), (944, 10))
最后,使用训练出的数据给出推荐电影
In [78]:
prediction = X_trained @ theta_trained.T
my_preds = prediction[:, 0] + Y.mean()
idx = np.argsort(my_preds)[::-1] # Descending order 取从后向前(相反)的元素
idx.shape
Out[78]:
(1682,)
In [79]:
# top ten idx
my_preds[idx][:10]
Out[79]:
array([4.19465938, 4.19323766, 3.98985134, 3.9420462 , 3.91425067,3.91276449, 3.90529067, 3.90447493, 3.78913731, 3.7832339 ])
In [80]:
for m in movie_list[idx][:10]:print(m)
Titanic (1997)
Star Wars (1977)
Raiders of the Lost Ark (1981)
Return of the Jedi (1983)
Shawshank Redemption, The (1994)
Empire Strikes Back, The (1980)
Braveheart (1995)
Good Will Hunting (1997)
Schindler's List (1993)
Godfather, The (1972)In [76]:```python
X_trained, theta_trained = deserialize(fmin.x, movies, users, features)
X_trained.shape, theta_trained.shape
Out[76]:
((1682, 10), (944, 10))
最后,使用训练出的数据给出推荐电影
In [78]:
prediction = X_trained @ theta_trained.T
my_preds = prediction[:, 0] + Y.mean()
idx = np.argsort(my_preds)[::-1] # Descending order 取从后向前(相反)的元素
idx.shape
Out[78]:
(1682,)
In [79]:
# top ten idx
my_preds[idx][:10]
Out[79]:
array([4.19465938, 4.19323766, 3.98985134, 3.9420462 , 3.91425067,3.91276449, 3.90529067, 3.90447493, 3.78913731, 3.7832339 ])
In [80]:
for m in movie_list[idx][:10]:print(m)
Titanic (1997)
Star Wars (1977)
Raiders of the Lost Ark (1981)
Return of the Jedi (1983)
Shawshank Redemption, The (1994)
Empire Strikes Back, The (1980)
Braveheart (1995)
Good Will Hunting (1997)
Schindler's List (1993)
Godfather, The (1972)