老卫带你学—SVM支持向量机
学习目标：
- 理解支持向量机的知识结构
- 理解支持向量机的原理与目标
- 理解算法推导的核心过程和意义（关键是损失函数与约束条件的意义）
- 理解核函数的意义与方法
知识结构
hard margin SVM：可以容易的找到一条划分超平面来将两类分开；
soft margin SVM：不容易找到划分超平面，但是可以寻找到一条相对最好的；
Kelnel：将核函数应用于 SVM，增加其内积计算速度；（核函数只是一种计算方法，也可以用于其他方面）
对偶函数：将原来的问题转化为对偶形式，方便计算。
下面黄色的部分是重要的地方。
各种概念如下：
我们谈一谈支持向量机与逻辑回归的区别：
逻辑回归的损失函数是L=-ylog(y’)-(1-y)log(1-y’)
它所代表的含义就是，计算样本与划分面的距离损失，通过计算向量与边界法向量的内积来求距离（也就是投影），判断这个样本是否分类正确
而SVM对其进行一定的改造，认为超过一定的距离的样本是没有损失的，只需要计算划分面周围的向量，这些向量我们也称为支持向量
这就是逻辑回归与SVM最核心的区别
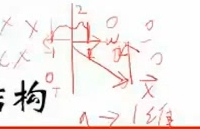（逻辑回归图）
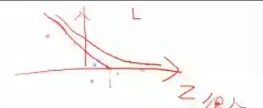（SVM函数图像）
SVM的目标函数是：
左边的是原始SVM的目标函数，右边是对于松弛变量所加入的代价变量
下面的约束条件也引进松弛变量，使函数间隔加上松弛变量大于等于1.
这里要注意一个地方，在hard margin中没有损失函数，而在逻辑回归中损失函数与目标函数一样
下面我们看一下划分超平面：
但是SVM仅仅只需要考虑关于那几个支持向量（红线包括），不需要将所有的样本进行计算。
我们将分类问题中的输入空间与特征空间看作两个空间
老卫语录：输入空间为欧式空间或离散空间；特征空间为欧式空间或希尔伯特空间
线性可分支持向量机（Hard Margin SVM）与线性支持向量机（Soft Margin SVM）将输入空间与特征空间元素一一对应；
非线性支持向量机将输入空间通过非线性映射映射为特征空间。
总体来说，支持向量机的学习都是在特征空间中进行
超平面的函数与决策函数如下
其中W是超平面的法向量，法向量指向的是正类；
x就是样本向量；
b为截距。
φ(x)就是前面说的映射函数
下面我们开始推导目标函数：
在这里我们将min后面的一坨通过约束条件处理掉，因为约束条件是大于等于1，而目标函数中是min，我们干脆直接取1
然后求W分之1的最大值，其实就是求W的平方的最小值。1/2是为了后面的求导方便而设计的。
W的绝对值就是L1正则化；W的平方就是L2正则化。
对偶函数
有时候为了计算方便，我们将原始问题转换为对偶问题来解决。（详情请看蓝皮书p103）
转换对偶函数
L对W，b分别求偏导
然后再将偏导结果带入上式
继续求对a的极大
添加负号，转化为min问题
最后可以由a求得w，b的解。
线性支持向量机
对于有的时候，我们的问题是线性不可分的，我们需要对相关细节进行改造。
通常情况是，训练数据中有一些特异点，将这些特异点去除后，剩下大部分的样本点组成的集合还是线性可分的。
老卫语录：线性不可分指的是某些样本点不能满足函数间隔大于等于1的约束条件。
为了解决这样的问题，我们对每个样本引进一个松弛变量，使函数间隔加上松弛变量大于等于1.
所以线性SVM的目标函数如下：
和Hard Margin问题一样，为了计算方便，我们将原始问题转化为对偶函数，然后对w，b，松弛变量进行求导。
所以线性支持向量机的学习算法如下：
LR与SVM的损失函数图像对比：
非线性支持向量机
有的时候我们的问题不是线性的，我们需要通过映射函数φ，将非线性问题转化为线性问题，数据从低维映射至高维。
对于核函数的类别可以看蓝皮书p122常用的核函数。
LR与SVM的区别：
- 损失函数不同，SVM采用的Hinge损失，而LR采用的是交叉熵损失；
- SVM仅考虑支持向量；
- SVM有约束条件；
- LR的可解释性更强；
- SVM不能给出概率结果；
- SVM对非线性问题采用核函数的方法速度更快。
