前言

昨天挖了个坑，那么今天的话把坑填上，只要是实现Sort算法和Yolov5-Lite的一个整合。当然先前的话，我们在Yolov3–Tiny的时候，也做了一个，不过当时的话，有几个问题没有解决。第一就是当时以中心点进行预测的，这样做的结果就是如果目标框的波动比较大的话，影响会很大，同时，当时设计是为了应对直线旋转平移这样的运动进行捕捉。所以效果比较差。同时就是对于目标点的匹配不合理。那就是，我是按照，当预测点和识别点进行距离计算，计算当前点的最小距离。在同一个类别之下，但是这里有个问题，就是，假设有一个的A，和点B，C，由于B点先进行计算，那么假设A，B匹配了，当C进来的时候，由于C可能和A点的距离更小，但是由于B，A已经匹配导致C没有和A匹配。那么这样一来明明C是最合适A的，但是由于B先来，导致A和B先匹配了（淦，有点像极了人生）

所以，这里的话，还是要引入匈牙利算法，当然这个算法的话，在先前的算法刷题专栏当中已经说过了，那么这里就不重复了，其实就是简单的应用。

项目结构

这里先说一下，这个项目的基本原理还是类似的：

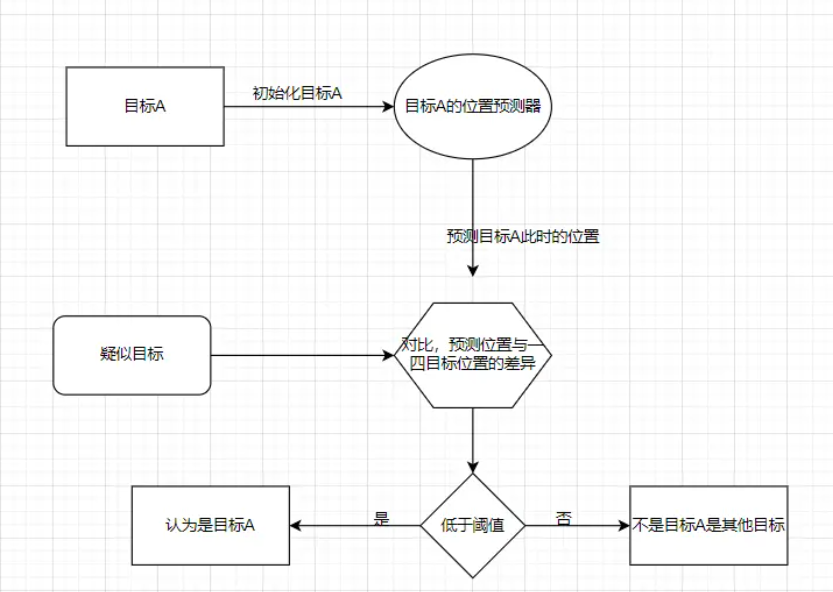
只是，现在匹配我们换成了匈牙利算法。

Sort算法实现

那么，在这里的话，我们先来实现Sort算法。本来是打算嫖个开源的做整合的，但是没想到，他们的代码有很多问题，改别人的bug,还不如自己手写，所以的话，这里的话，我自己手写了一个Sort算法。这里注意的是，Sort算法只是一个匹配算法，通过IOU，和卡尔曼滤波做预测，来匹配当前的跟踪器和新产生的目标框是不是同一个目标。如果你的目标识别算法不准确的话，也就是目标框不稳定，会不断生成新的目标框，那么你的Sort算法就会不断认为这是新的目标的。解决办法的话，可以考虑使用deepsort。 但是的话，我们这里是边缘设备，如果没有deepsort-lite的话实在是不好搞。而且，比如一些简单场景，比如车流量检查，行人检测啥的，机位固定倒也用不上。

卡尔曼跟踪器

那么首先，在这里要实现的就是卡尔曼跟踪器。
这里的话，原理就不扯了，我这里都提到好几次了。

import numpy as np
from filterpy.kalman import KalmanFilter
import cv2
from sort.utils import convert_bbox_to_z, convert_x_to_bbox
np.random.seed(0)@DeprecationWarning
class ObjectTrackerKF:"""这个滤波是只跟踪中心点坐标，不过，还是会还原为[x1,y1,x2,y2]的"""def __init__(self,bbox, dt=1, sigma=10):# 每次创建新的kalman滤波器时，计数ID都会加1self.id = 0self.hit_streak = 0self.bbox = bbox# 自上次未匹配成功，经过的帧数self.time_since_update = 0# 自上次未匹配成功，连续成功匹配的帧数self.hit_streak = 0self.dt = dtx_init, y_init = (bbox[0]+bbox[2])/2 ,(bbox[1]+bbox[3])/2# 状态向量，包含位置和速度信息self.state = np.array([[x_init], [y_init], [0], [0]], np.float32)# 系统矩阵，将状态向量映射为下一时刻的状态向量self.A = np.array([[1, 0, self.dt, 0],[0, 1, 0, self.dt],[0, 0, 1, 0],[0, 0, 0, 1]], np.float32)# 测量矩阵，将状态向量映射为测量向量self.H = np.array([[1, 0, 0, 0],[0, 1, 0, 0]], np.float32)# 过程噪声，表示模型中未考虑的外部因素产生的偏差self.Q = np.array([[self.dt ** 4 / 4, 0, self.dt ** 3 / 2, 0],[0, self.dt ** 4 / 4, 0, self.dt ** 3 / 2],[self.dt ** 3 / 2, 0, self.dt ** 2, 0],[0, 0, 0, self.dt ** 2]], np.float32) * sigma ** 2# 测量噪声，表示测量器的误差self.R = np.array([[1, 0],[0, 1]], np.float32) * sigma ** 2# 卡尔曼滤波器初始化self.kf = cv2.KalmanFilter(4, 2, 0)self.kf.statePost = self.stateself.kf.transitionMatrix = self.Aself.kf.measurementMatrix = self.Hself.kf.processNoiseCov = self.Qself.kf.measurementNoiseCov = self.Rdef predict(self):self.state = self.kf.predict()t = self.state[:2].reshape(-1)t = list(t)w = self.bbox[2] - self.bbox[0]h = self.bbox[3] - self.bbox[1]box = [(t[0]-w/2),t[1]-h/2,t[0]+w/2,t[1]+h/2,self.bbox[4]]self.bbox = boxif self.time_since_update > 0:self.hit_streak = 0return self.bboxdef update(self,bbox):x, y = (bbox[0]+bbox[2])/2 ,(bbox[1]+bbox[3])/2self.time_since_update = 0# 表示连续匹配成功的次数加一if(self.hit_streak<=30):self.hit_streak+=1self.kf.correct(np.array([[x], [y]], np.float32))return self.state[:2].reshape(-1)class KalmanBoxTracker(object):# 利用bounding box初始化Kalman滤波轨迹def __init__(self, bbox):self.id = 0#注意这里的bboxs是[x1,y1,x2,y2,conf]是list类型self.bbox = bbox# 定义恒定速度模型，7个状态变量和4个观测输入self.kf = KalmanFilter(dim_x=7, dim_z=4)# 状态向量 X = [检测框中心的横坐标，检测框中心的纵坐标，检测框的面积，长宽比，横坐标速度，纵坐标速度，面积速度]# SORT假设一个物体在不同帧中检测框的长宽比不变，是个常数，所以速度变化只考虑横坐标、横坐标、检测框面积self.kf.F = np.array([[1, 0, 0, 0, 1, 0, 0],[0, 1, 0, 0, 0, 1, 0],[0, 0, 1, 0, 0, 0, 1],[0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0],[0, 0, 0, 0, 0, 1, 0],[0, 0, 0, 0, 0, 0, 1]])self.kf.H = np.array([[1, 0, 0, 0, 0, 0, 0],[0, 1, 0, 0, 0, 0, 0],[0, 0, 1, 0, 0, 0, 0],[0, 0, 0, 1, 0, 0, 0]])# R是测量噪声的协方差矩阵，即真实值与测量值差的协方差# R = diagonal([1, 1, 10, 10])self.kf.R[2:, 2:] *= 10.# [[ 1.  0.  0.  0.]#  [ 0.  1.  0.  0.]#  [ 0.  0. 10.  0.]#  [ 0.  0.  0. 10.]]# P是先验估计的协方差，对不可观测的初始速度，给予高度不确定性# P = diagonal([10，10，10，10，1000，1000，1000])self.kf.P[4:, 4:] *= 1000.self.kf.P *= 10.# [[   10.     0.     0.     0.     0.     0.     0.]#  [    0.    10.     0.     0.     0.     0.     0.]#  [    0.     0.    10.     0.     0.     0.     0.]#  [    0.     0.     0.    10.     0.     0.     0.]#  [    0.     0.     0.     0. 10000.     0.     0.]#  [    0.     0.     0.     0.     0. 10000.     0.]#  [    0.     0.     0.     0.     0.     0. 10000.]]# Q是系统状态变换误差的协方差# Q = diagonal([1, 1, 1, 1, 0.01, 0.01, 0.0001])self.kf.Q[