TOC

第二章 数据预处理与短时交通流量特性分析

2.1 数据来源

数据记录了明尼苏达州双子城19条高速环城公路一整年的交通流量，交通流量数据采样间隔为30秒(采用2018年6月1日至8月31日期间，采集间隔为5分钟，选取公路上的5个车辆检测站点的交通流量数据)。由于交通流会受到天气因素的影响，因此实验中还引入了天气数据。该数据记录了美国明尼苏达州圣保罗国际机场气象监测站一整年的各种天气状况，天气状况采样间隔同样为30秒(采用2018年6月1日至8月31日期间，采集间隔为5分钟，圣保罗国际机场气象监测站的天气数据如连接所示https://download.csdn.net/download/CSDNXUXIAOYAO/87724196)。5 个车辆检测站点（以下简称站点）分别记作p1、p2、p3、p4、p5。本文的目标是预测p3车辆检测站点未来时刻的交通流量，因此将p3车辆检测站点称为目标站点，其余车辆检测站点称为上下游站点。圣保罗国际机场气象监测站（以下简称气象站）记作Q。

2.2 数据预处理

2.2.1 缺失数据补齐

常见的补齐方法有历史值替代法、平均值插补法等，每种方法各有优缺点，需根据数据缺失程度及特点，选取合适的方法。历史值替代法可用于交通流量数据连续大量缺失，交通流量具有周期性，对于当前缺失的数据可直接用历史数据进行替代。由于本文的交通流量数据没有出现大面积连续缺失，只是零星时刻出现空值，同时交通流量的变化具有连续性，因此采用前后相邻值的平均值插补法处理空缺数据，确保数据的完整性及实用性，便于后续的交通流量数据特性分析与预测。
本文利用数据缺失时刻t的前后相邻时刻平均值补齐空缺，公式如(2-1)所示。

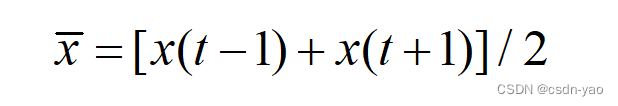
其中，x ̅为前后相邻时刻的平均值，t为任意时刻。

相邻前后值的平均值插补法 python代码：

import pandas as pd
df1=(data.fillna(method='ffill')+data.fillna(method='bfill'))/2

也可以使用线性插值法进行缺失值补齐 python代码：

df1=data.interpolate(method='linear',limit_direction='forward',axis=0)

2.2.2 归一化

由于使用的交通与天气数据中的各个属性具有不同的量纲标准，这可能会影响后续预测模型的准确性，所以需将各个属性的值约束到一个相同的取值范围中。
本文采用max-min线性归一化法将数据约束在[0,1]范围内，归一化公式如(2-4)所示。经过归一化处理的数据，各属性拥有相同的数量级，避免出现数量级大的数据所占权重大的现象，可提高实验的准确性。

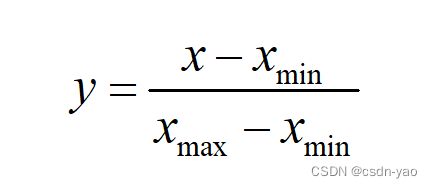
其中， x为原始属性值， y为归一化后属性值， xmax为原始属性值中的最大值， xmin为原始属性值中的最小值。
max-min归一化 python代码：

import numpy as np
import pandas as pd
for i in list(df1.columns):Max=np.max(df1[i])Min=np.min(df1[i])df1[i]=(df1[i]-Min)/(Max-Min)

2.3 短时交通流特性分析

2.3.1 基于K-means的差异性分析

交通流量数据是时间序列数据，其聚类过程比较特殊。本节采用p3目标站点2018年6月1日至8月31日期间的交通流量数据，样本时间间隔为5分钟，共计26494个时间点，因此该数据具有维度高且属性单一的特点。所以本文先将高维的交通流量数据降维，将高维度的交通流量按照一天的时间长度，分段成一条条样本，每条样本开始与结束的时间为0:00至23:55，样本时间间隔为5分钟，共计288个时间点。其中每条样本代表一种交通流类别，这样每个样本拥有相同的起始终止时间点，然后将样本的每个时间点作为一个特征，通过k-means算法实现多特征样本间的聚类，再从日期的角度来解释最终的聚类结果。k-means算法中的聚类中心数决定最终的聚类效果，因此本文通过轮廓系数法选取合理的k值。
图2-3中（a）、（b）、（c）、（d）分别为k取2、3、4、5下的轮廓系数值，横坐标为每个样本的轮廓系数值，纵坐标为k种不同类别的样本。图（a）中显示k为2时，聚类中的大多数样本具有较大的轮廓系数值（轮廓系数值大于0.6），这表示聚类样本间分离效果较好，但随着k值的增大，各样本的轮廓系数整体在减小，甚至开始出现负值，这表示聚类样本间分离效果不理想。因此判定k值取2为最优。

K-means与轮廓系数 MATLAB代码：

load matlab;X=A(:,:);[C,S]=subclust(X,0.5,[],[1.25 0.5 0.15 0]);
[idx2 cent]=kmeans(X,2,'dist','city','display','iter');
[idx3 cent]=kmeans(X,3,'dist','city','display','iter');
[idx4 cent]=kmeans(X,4,'dist','city','display','iter');
[idx5 cent]=kmeans(X,5,'dist','city','display','iter');
figure(1)
[silh2,h2]=silhouette(X,idx2,'city');
figure(2)
[silh3,h3]=silhouette(X,idx3,'city');
figure(3)
[silh4,h4]=silhouette(X,idx4,'city');
figure(4)
[silh5,h5]=silhouette(X,idx5,'city');

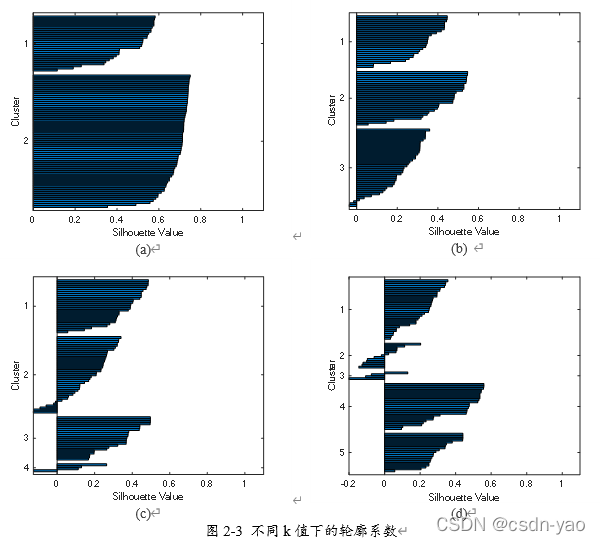
图2-4中（a）、（b）、（c）、（d）分别为k取2、3、4、5下的聚类结果，横坐标为时间，纵坐标为交通流量值。从4种不同k值的聚类结果中可直观且全面地看出不同聚类结果中的交通流量拥有相似的变化规律，仅存在数值大小的差异。相比于（a）中的聚类结果，其它聚类结果中新增的交通流量种类更像是（a）中两种交通流量值的整体上移或下降。这也表明了k值取2最为合理

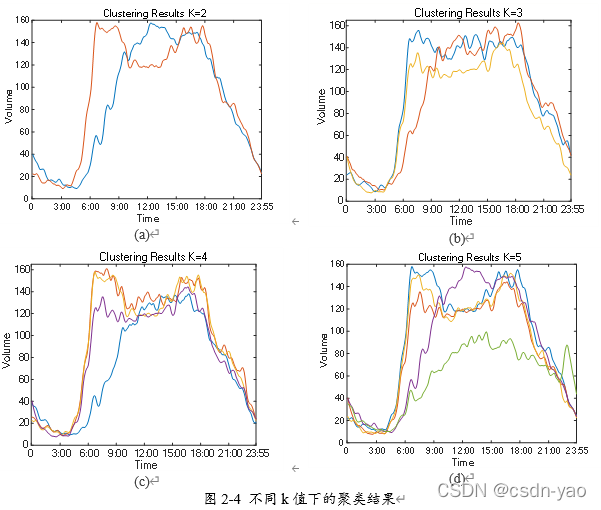
通过图2-3不同k值下的轮廓系数以及图2-4不同k值下的聚类结果分析可知，当k值取2时的聚类结果为最优。因此将交通流量划分为两种类别。

下面统计每种交通类别随星期变化的分布情况，结果如表2-1所示:
下面将具体分析两种类别交通流量的3点不同之处。
（1）高峰数量的差异
图2-5为k取2时的聚类结果。图中展示了两种变化趋势不同且各自特征明显的交通流量类别。类别2交通流量存在明显的早晚高峰，早高峰出现在7点到9点之间，晚高峰出现在16点到18点之间。这是因为交通流量受到居民出行规律的影响，多数上班族或学生工作日遵循 “早九晚五”的作息习惯。类别1交通流量没有明显的早、晚高峰，只存在单个高峰，高峰出现在中午12点左右。这也很符合多数人非工作日休息或娱乐，因此选择不出行或者避开早晚高峰出行的规律。

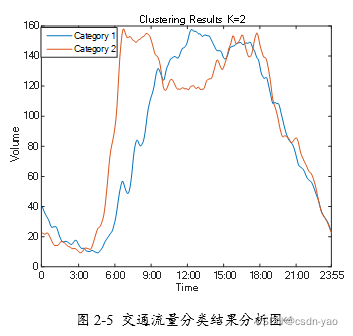
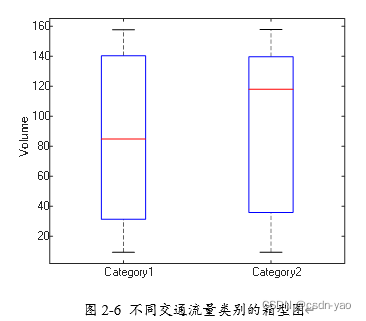
（2）交通流量值的差异
图2-6为两种类别交通流量的箱型图，类别1交通流量数据的中位数明显小于类别2交通流量数据的中位数，这代表类别1样本数据的平均值较小，整体交通流量值小于类别2样本。这很符合常规，即非工作日的交通流量小于工作日。

（3）交通流量变化趋势剧烈程度的差异
图2-7中分别展示了两种类别交通流量的一阶差分绝对值，其值可衡量交通流量变化趋势的剧烈程度，从图中可以看出，类别1非工作日交通流量数据的一阶差分绝对值整体小于类别2工作日，这表明在一天之中，类别1非工作日交通流量的变化趋势略平缓，而类别2工作日交通流量的变化趋势较为剧烈。

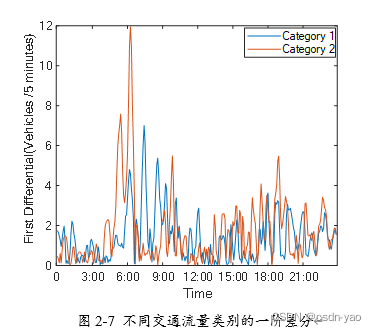
综上所述，类别2工作日与类别1非工作日的交通流量相比，不管是高峰个数、整体交通流量值的大小，还是交通流变化趋势的剧烈程度，均存在一定的差异。
本节利用k-means算法将交通流分为两种类别，验证得出两种类别分别对应非工作日与工作日下的交通流，同时发现工作日与非工作日的交通流量存在很大区别，所以本文考虑分别预测工作日和非工作日的交通流量数据，以提高预测精度。

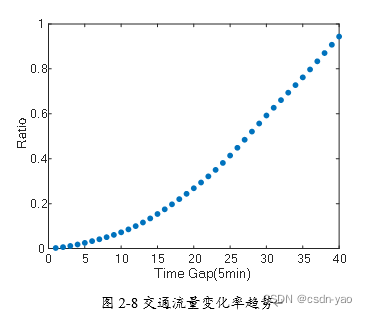
2.3.2 基于变化率趋势的时间邻近性分析

图2-8展示了交通流量变化率的趋势与时间间隔间的关系，横轴表示两个时间点之间的间隔，纵轴表示不同时间间隔下的交通流量变化率均值。从图2-8中可以看出，邻近间隔的交通流量变化率较小，但是当时间间隔增大时，交通流量变化率也随之增大。这表示交通流量具有时间邻近性。

2.3.3 基于相关系数的空间关联性分析

图2-9散点图矩阵中对角线位置为5个站点的交通流量直方图，x轴表示交通流量值，y轴表示交通流量值出现的次数。其余位置分别为p1至p5站点序列中第i个站点与第j个站点间的散点图，若图中散点呈现细长带状，表明两个变量具有强线性相关关系，若呈现短粗团状，表明两个变量间线性相关性弱或不相关。


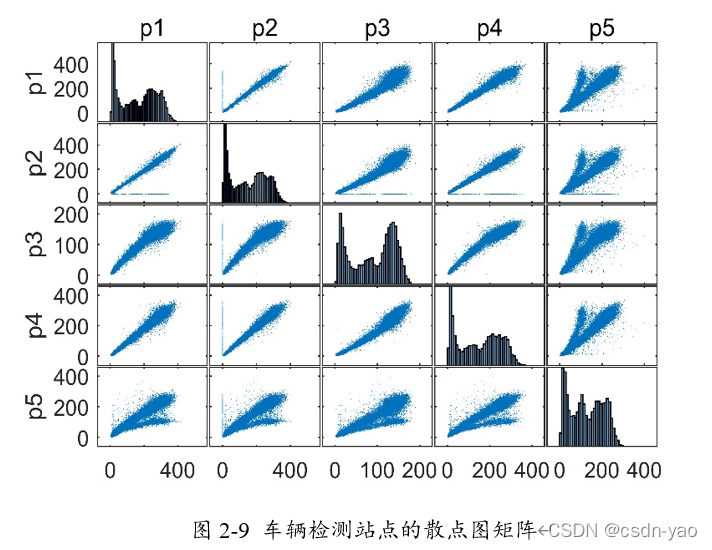
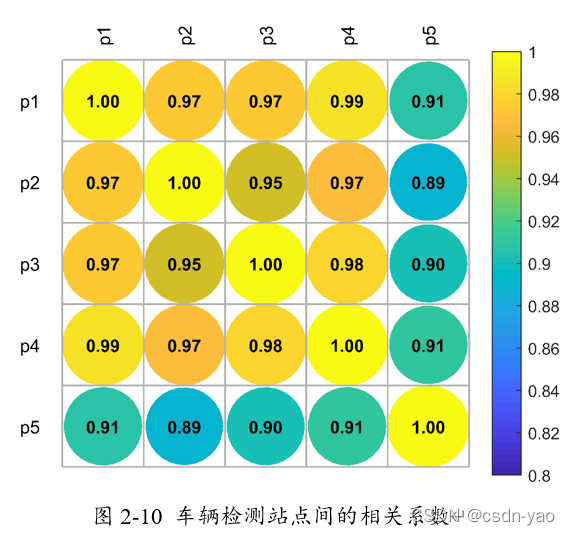
从图2-9和图2-10中可观察到，5个相邻站点：p1、p2、p3、p4、p5具有很强的线性相关性关系。后续实验中将考虑将相邻站点的交通流量数据带入预测模型，进而提高模型的预测准确率。

2.3.4 基于天气因素的随机性分析

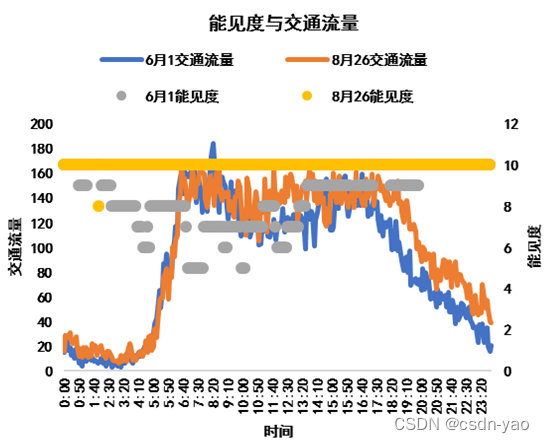
图2-11展示了站点p3于6月1日、8月26日在不同能见度下的交通流量对比情况。图2-11中显示，在6月1日能见度低于8月26日的情况下，交通流量也略低。由于天气对交通流的影响比较复杂，目前还无法确定两者之间确切的关系。但是通过经验可知，雨天或雾天的能见度低，道路湿滑，司机为了行车安全，一般会降低车速，那么这种天气情况必然会改变交通运行状况。因此，本文后续考虑在预测模型中增加天气因素，利用深度网络的强大的特征提取功能，挖掘天气因素与交通流量间的隐含关系，从而提升模型预测精度。

2.4 短时交通流量预测结果评估指标

时间序列预测模型预测结果的有效性，不能简单地使用一个指标来衡量，需要综合考虑多个指标。本文主要选择平均绝对误差、均方根误差、平均绝对百分比误差三个评价指标。具体评价指标如下，其中 表示第i时刻实际交通流量实际值， 表示第i时刻模型输出的交通流量预测值， 表示待评估的交通流时间序列的长度。三个评价指标的评估值越低，表明预测结果越好。
平均绝对误差(Mean Absolute Error，MAE)是实际交通流量与预测交通流量间差的绝对值总和，除以待评估的交通流时间序列长度的结果。平均绝对误差将实际交通流量与预测交通流量间的误差取绝对值，因此避免了求误差总和时正负相消，可以较好反应预测结果的精度。并且平均绝对误差值越低，则表明预测结果越好。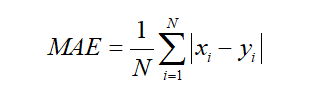
均方根误差(RMSE)为实际交通流量与预测交通流量间差的平方总和除以待评估的交通流时间序列长度 的结果再开方。均方根误差将实际交通流量与预测交通流量间的误差放大，因此可以表明预测交通流量与实际交通流量间的离散程度，反应预测结果的精度。并且均方根误差的值越低表明预测结果越好。

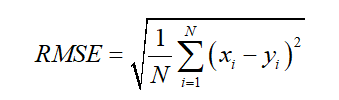
平均绝对百分比误差（MAPE）为实际交通流量与预测交通流量间的差与实际交通流量的比值绝对值除以待评估的交通流时间序列长度 的结果。平均绝对百分比误差计算了预测交通流量与实际交通流量间的相对误差，表明了预测交通流量与实际交通流量间的平均偏离程度，可以较好反应预测结果的精度，并且平均绝对百分比误差的值越低表明预测结果越好。

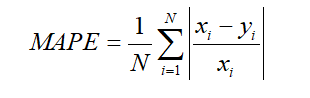
第三章 基于时空关联的短时交通流预测

3.1 基于时空关联LSTM的交通流预测模型框架

仅考虑交通流时间相关性的预测模型，只利用目标站点本身的历史数据预测下一时刻交通流量，模型预测精度较低。考虑到交通流还具有空间关联性，因此利用目标站点与上下游站点间的空间关联关系，使得预测模型不仅可以学习目标站点自身的交通流变化特征，还可以通过局部相关系数加权来学习上下游站点的交通流变化特征，从而提高预测精度。

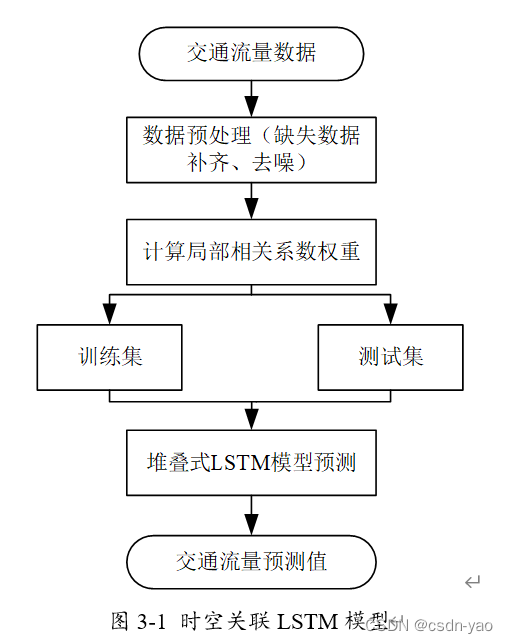
3.2 实验设计与结果分析

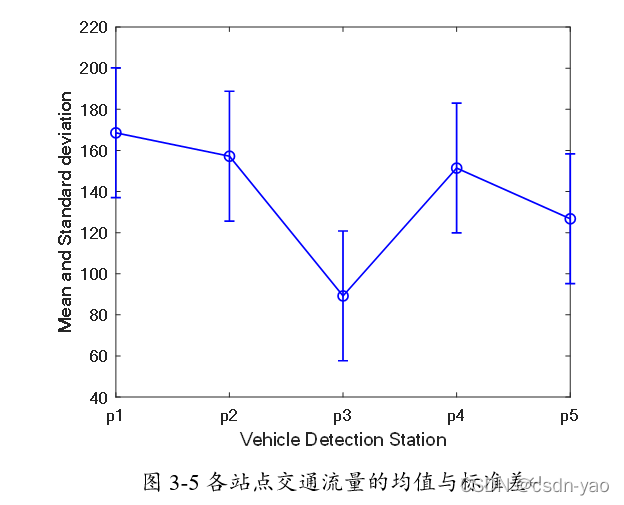
3.2.1 相关系数权重计算结果

从图中可以看出5个站点交通流量的均值与标准差均不相同，这是高速公路匝道驶入与驶出的车辆导致的。同时5个站点的交通流量标准差都较大，这表明交通流量的波动性较大，不确定性较高。

局部相关系数是计算两个时间序列每个时刻的相关系数，如计算两个相邻站点时间序列 ，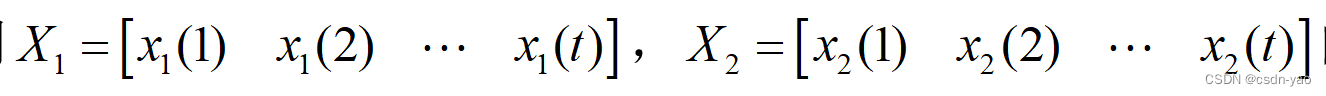
间的全局相关系数，则利用两个时间序列的整个时间段数值参与计算。
局部相关系数是计算两个时间序列时时刻刻的相关系数，如计算两个相邻站点 ，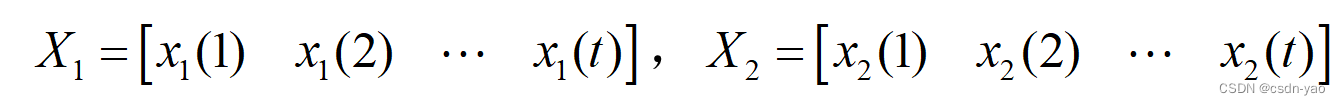
间的局部相关系数，即计算时间序列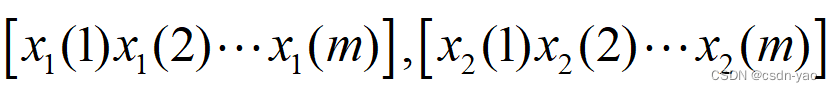
间的相关系数，其中m为滑动窗口长度，为计算两个时间序列每个时刻的相关性，步长取1。故以m的滑动窗口，1的步长，在整个时间序列中重复该过程，直到滑动窗口覆盖了所有时刻。
综上所述，全局相关系数是将两个时间序列的整个时间段的关系精简到一个值中，故全局相关系数高，不代表这两个时间序列每个时刻的相关性都高。因此本文选择计算上下游站点与目标站点间的局部相关系数作为各站点对应的空间上的权重。
图3-6中（a）、（b）、（c）、（d）分别展示了p1、p2、p4、p5站点与p3站点间的全局相关系数以及一天内的交通流量分布，可以看出p1、p2、p4站点与p3站点间的全局相关系数相同，p5站点与p3站点间的全局相关系数较小。虽然P1、p2、p4与p3间的全局相关性系数一致，但是每个时刻的相关系数依然存在差别。如果只考虑全局相关性，过于笼统，不能细致划分全天各个时刻上下游站点与目标站点的关系，故下面分析上下游站点与目标站点间的局部相关系数。

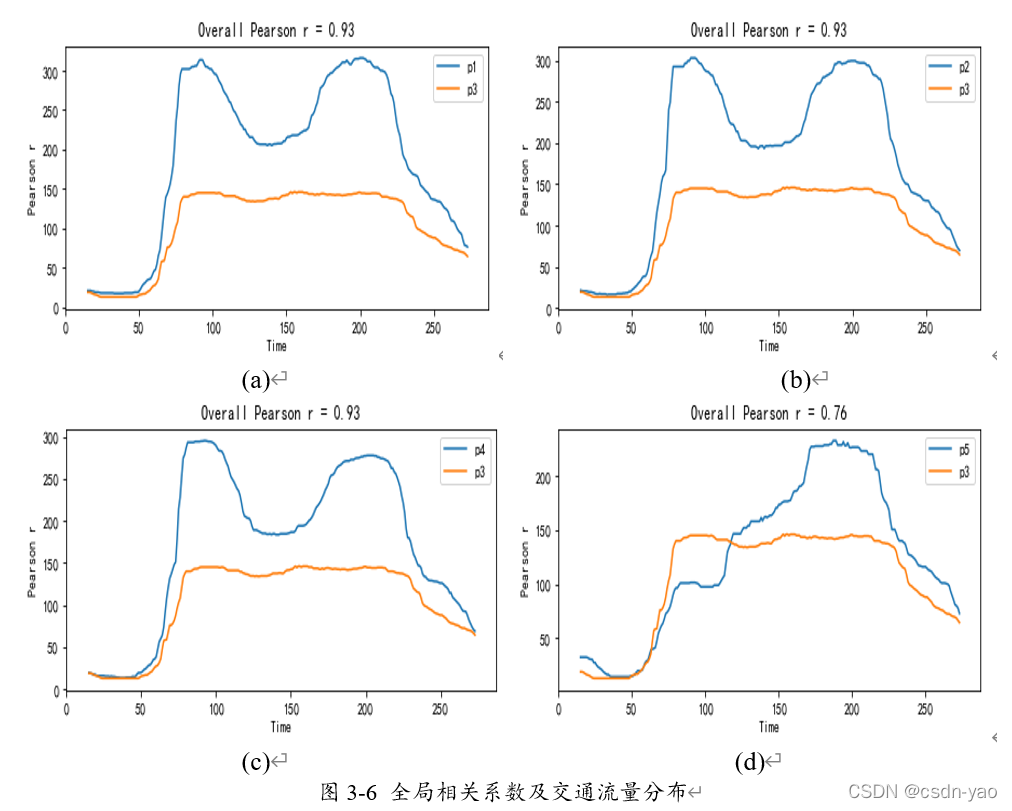
图3-7中(a)、(b)、©、(d)分别展示了上下游站点p1、p2、p4、p5与目标站点p3间的全天各时刻相关系数权重变化，在每个时刻目标站点p3与自身的相关系数都为1，这里不再展示。在一天中的不同时段，各站点的相关系数权重呈现的变化规律不同。并且在一天中的相同时段，各站点的相关系数权重大小也可能不同。这进一步证明局部相关系数权重相较于全局相关系数权重更能细致的量化各站点间的空间关联性。

求解局部相关系数的python代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as statsdf = pd.read_csv('p35.csv')
overall_pearson_r = df.corr().iloc[0,1]
print(f"Pandas computed Pearson r: {overall_pearson_r}")
# 输出：使用 Pandas 计算皮尔逊相关结果的 r 值：0.2058774513561943r, p = stats.pearsonr(df.dropna()['p5'], df.dropna()['p3'])
print(f"Scipy computed Pearson r: {r} and p-value: {p}")
# 输出：使用 Scipy 计算皮尔逊相关结果的 r 值：0.20587745135619354，以及 p-value：3.7902989479463397e-51# 计算滑动窗口同步性
f,ax=plt.subplots(figsize=(7,3))
df.rolling(window=30,center=True).median().plot(ax=ax)
ax.set(xlabel='Time',ylabel='Pearson r')
ax.set(title=f"Overall Pearson r = {np.round(overall_pearson_r,2)}")
plt.show()# 设置窗口宽度，以计算滑动窗口同步性
r_window_size = 11
# 插入缺失值
df_interpolated = df.interpolate()
# 计算滑动窗口同步性
rolling_r = df_interpolated['p5'].rolling(window=r_window_size, center=True).corr(df_interpolated['p3'])f,ax=plt.subplots(2,1,figsize=(14,6),sharex=True)
df.rolling(window=30,center=True).median().plot(ax=ax[0])
ax[0].set(xlabel='Time',ylabel='Traffic flow')
rolling_r.plot(ax=ax[1],color='orange')
ax[1].set(xlabel='Time',ylabel='Pearson r')
plt.suptitle("Traffic flow data and rolling window correlation")

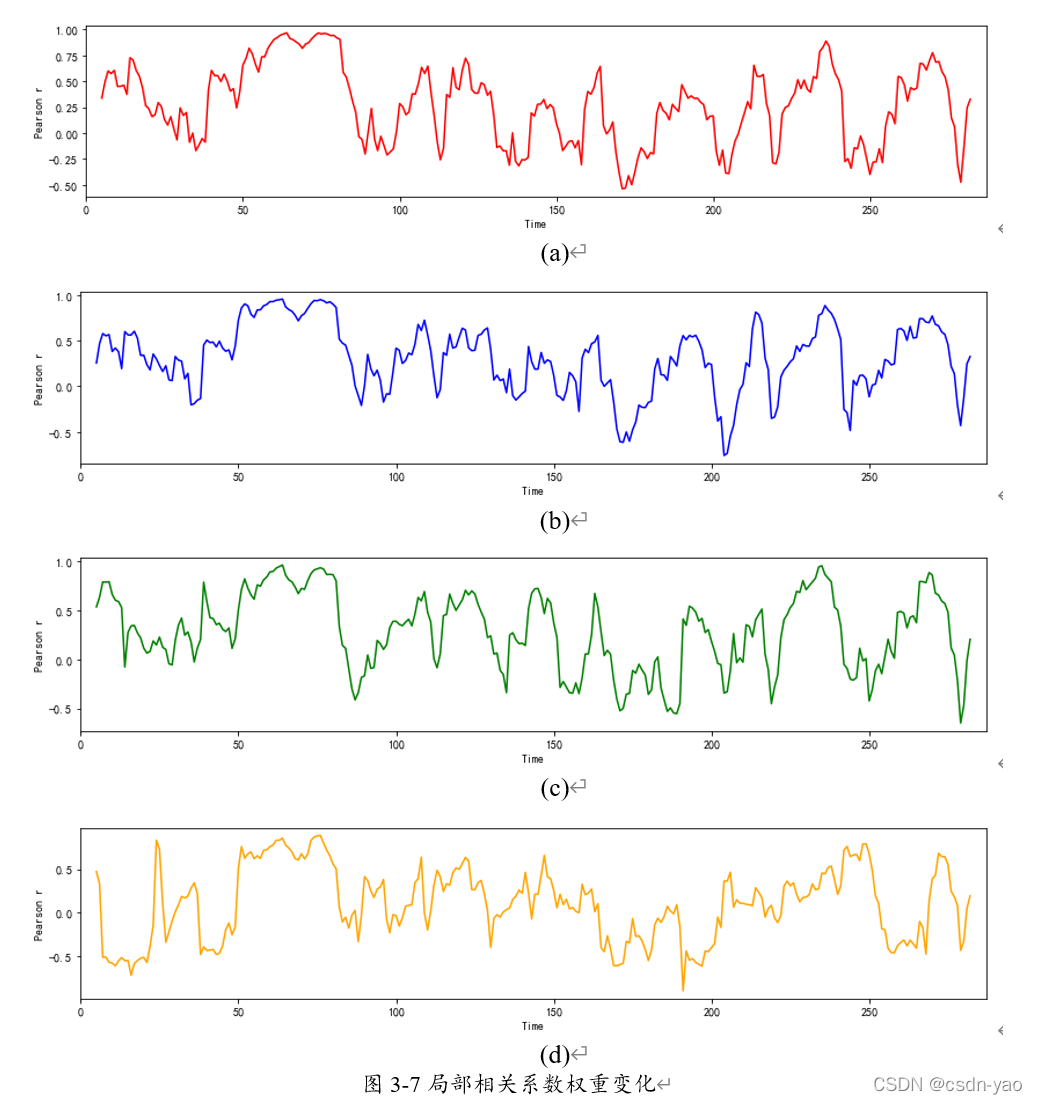
图3-9、3-10分别展示了工作日与非工作日下模型损失函数的变化过程，其横坐标为迭代次数，纵坐标为模型损失函数，即均方误差。图3-9与3-10中训练损失与验证损失均呈快速下降趋势并且最终趋于平稳，这表明模型的拟合状态良好，未出现过拟合与欠拟合。

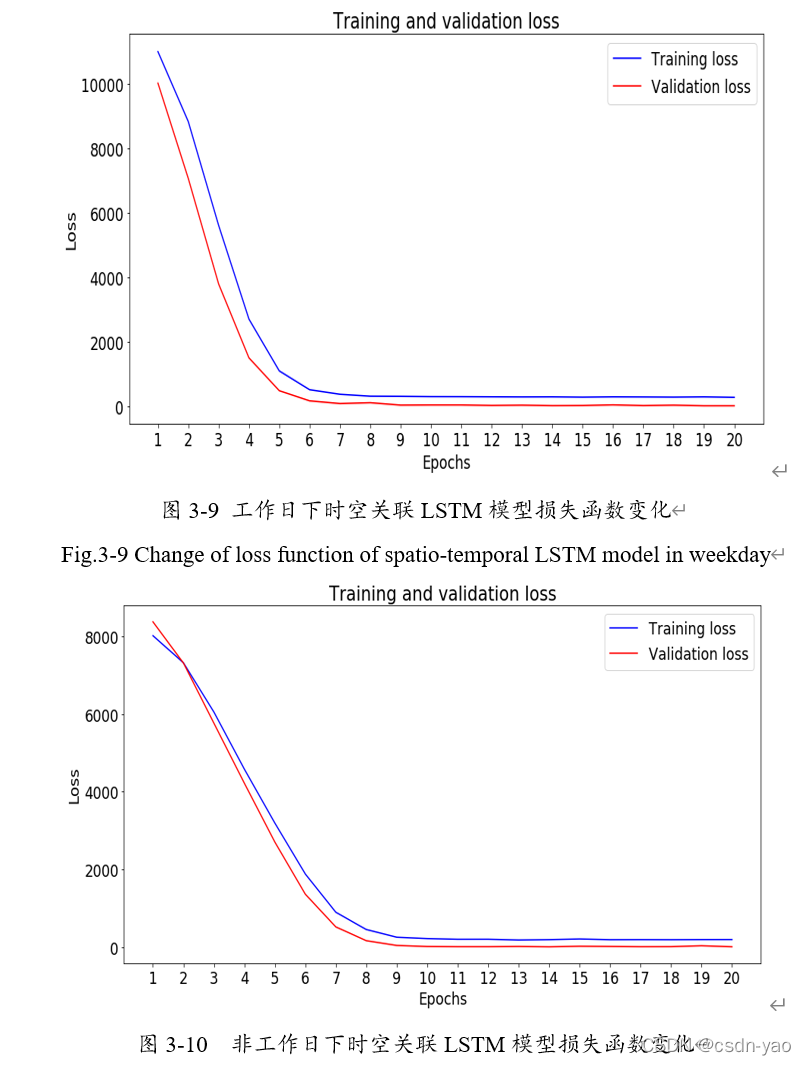
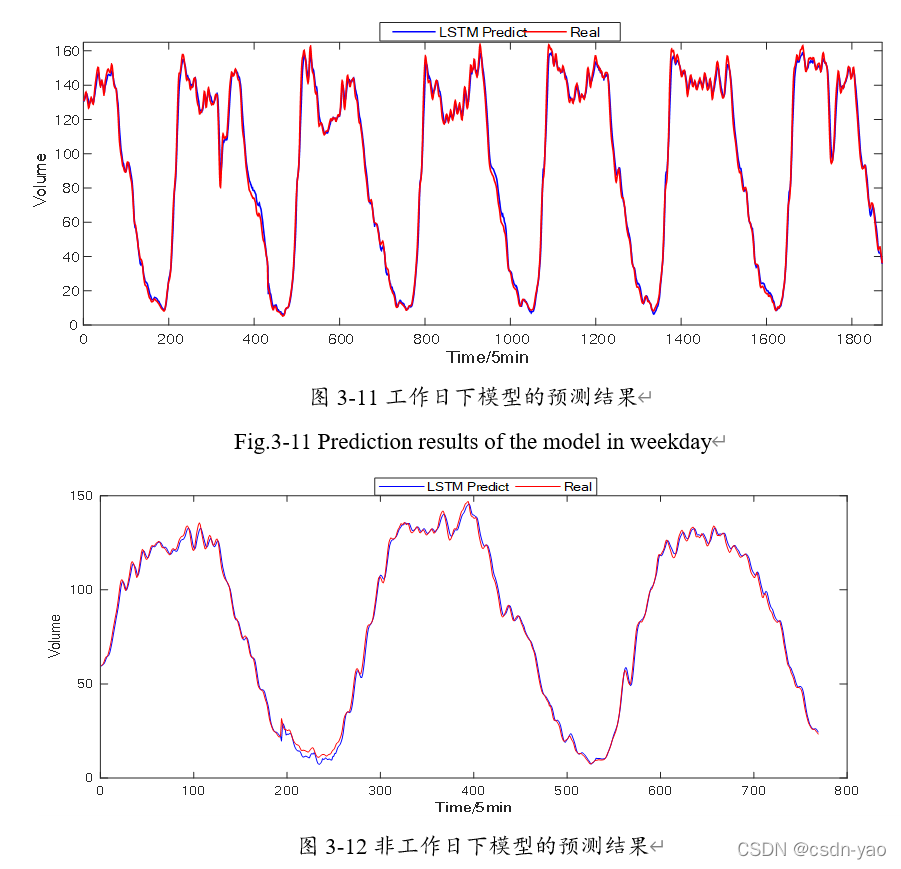
图3-11与图3-12分别展示了在工作日与非工作日两种交通流量类别下，时空关联LSTM模型预测值与真实值的对比图。其中横坐标为时间间隔（每5分钟），纵坐标为交通流量值。红色实线为交通流量真实值，蓝色实线为时空关联LSTM模型预测值。从图中可以看出，不论是工作日还是非工作日，时空关联LSTM模型基本捕捉交通流量总体变化趋势。

第四章 引入天气因素的短时交通流预测

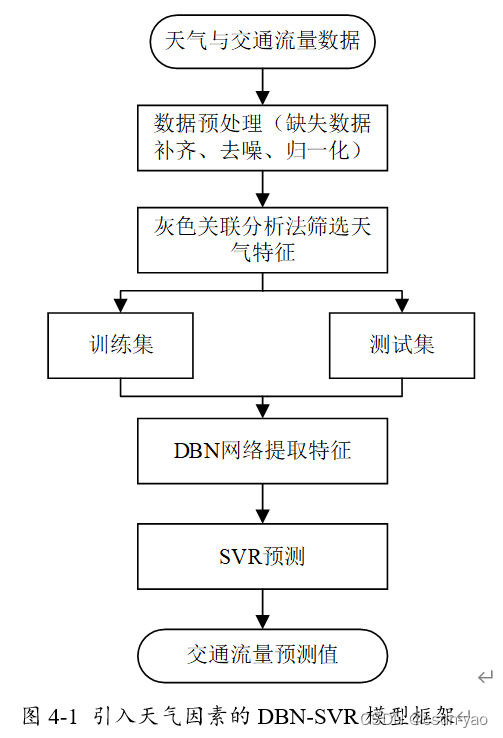
4.1 引入天气因素 的DBN-SVR模型框架

基于2.4.4小节的交通流特性分析，交通流数据的变化会受天气因素影响，呈现出随机性。本章提出引入天气因素的DBN-SVR模型。图4-1是引入天气因素的DBN-SVR模型的处理流程，包括数据预处理、灰色关联筛选天气特征、DBN网络提取特征、SVR预测。

4.2 实验设计与结果分析

4.2.1 特征选择结果

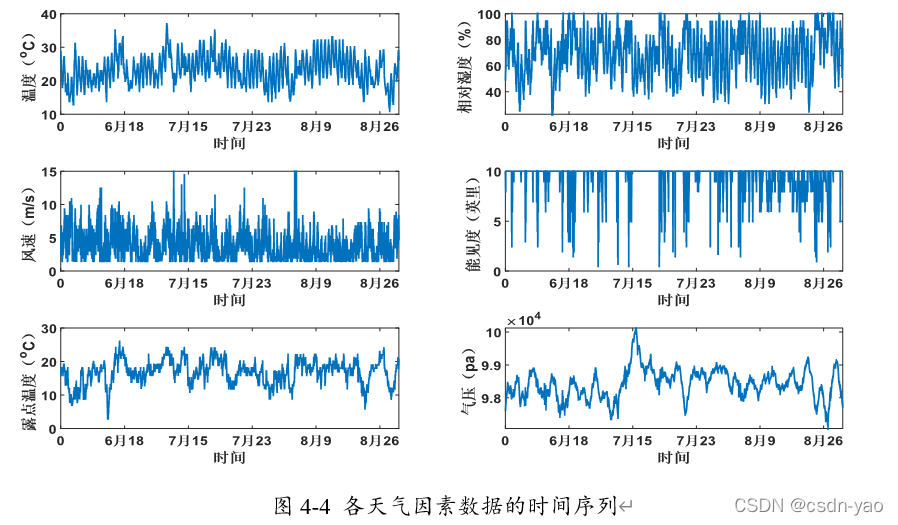
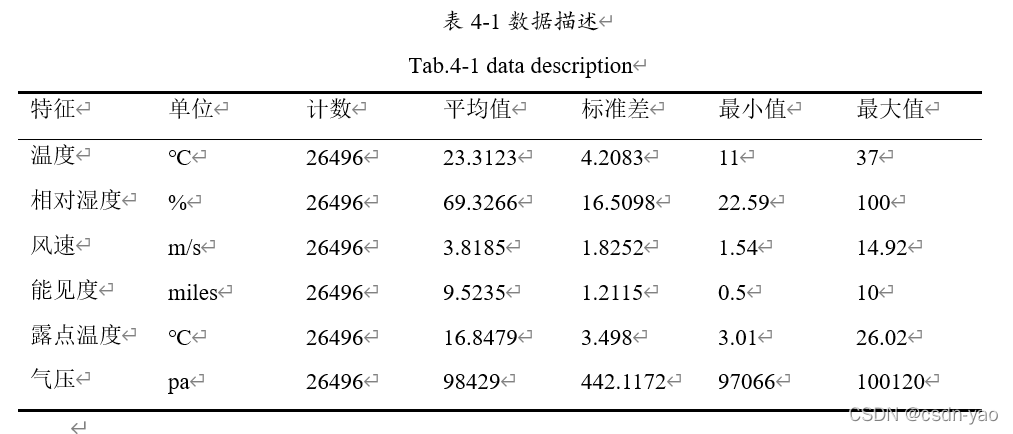
本文收集整理可量化的数值型天气数据有温度、相对湿度、风速、能见度、露点温度、气压。为了更清晰地观察每个天气因素的变化趋势，将其按时间序列绘制，如图4-4所示。各天气数据描述如表4-1所示。


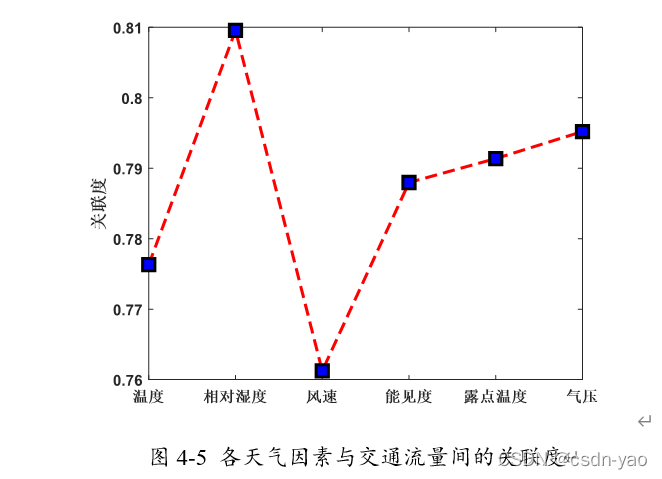
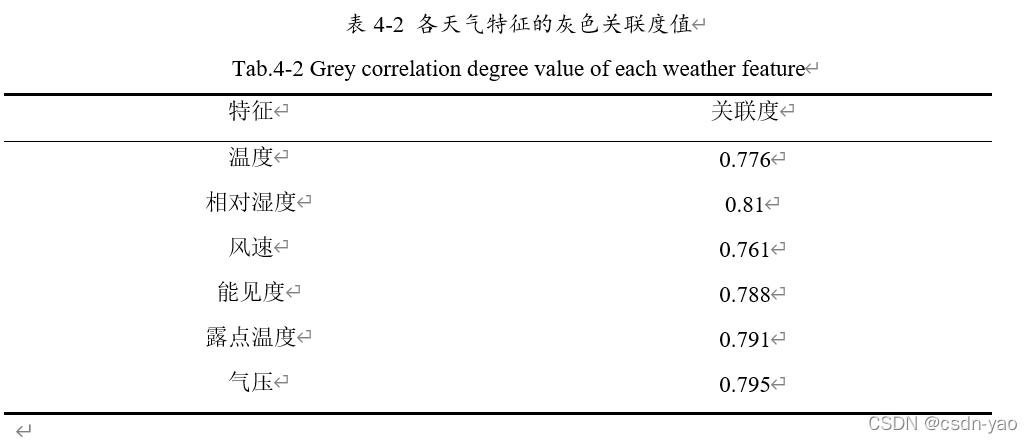
将上述天气数据与p3站点的交通流量数据进行灰色关联分析，结果如图4-5、表4-2所示。

4.2.2 引入天气因素的DBN-SVR模型预测结果

图4-6与图4-7分别展示了在工作日与非工作日两种交通流量类别下，DBN-SVR模型与SVR模型预测值与真实值的对比图。其中横坐标为时间间隔（每5分钟），纵坐标为交通流量值。红色实线为交通流量真实值，蓝色实线为DBN-SVR模型预测值，绿色实线为SVR模型预测值。从图中可以看出，不论是工作日还是非工作日，DBN-SVR模型基本捕捉交通流量总体变化趋势，而SVR模型在交通流量剧烈抖动的情况下，预测效果较差。

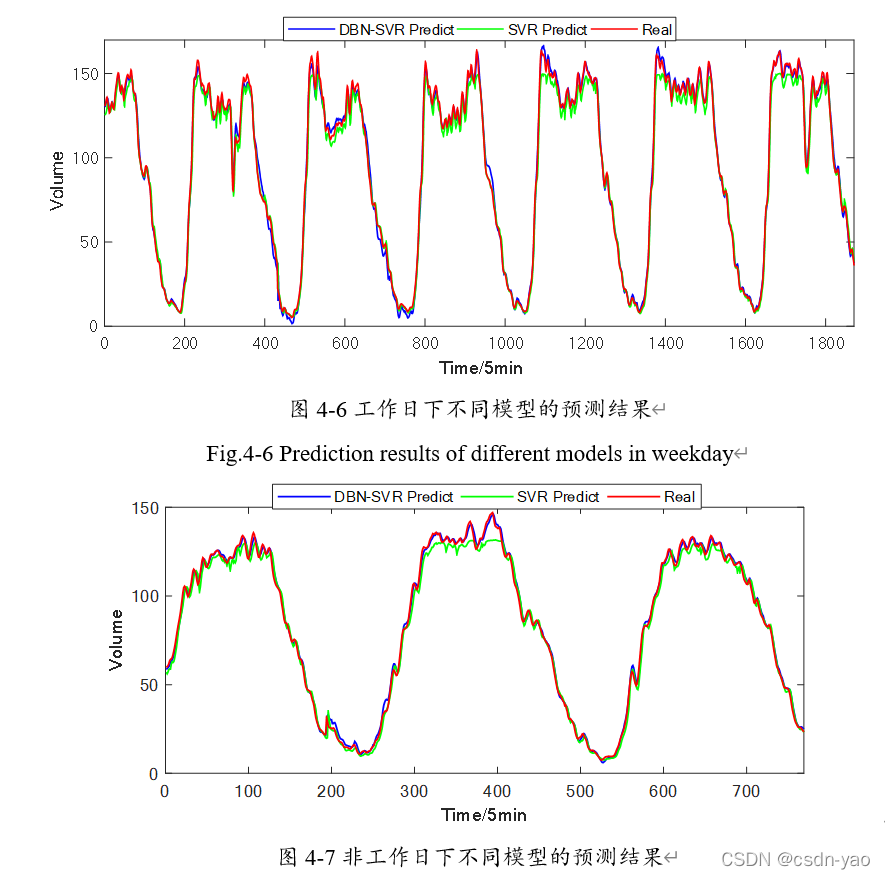
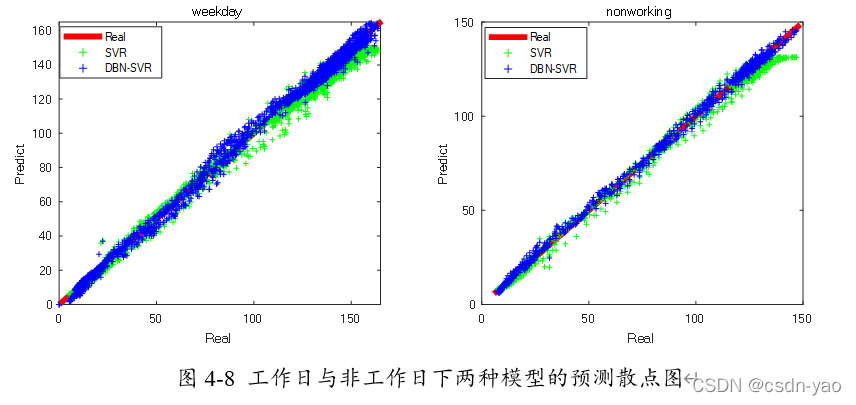
图4-8分别展示了工作日与非工作日下DBN-SVR模型、SVR模型的预测散点图，横轴为交通流量真实值，纵轴为各模型的交通流量预测值，红色实线表示最佳拟合效果，即预测值等于真实值。蓝色散点的横坐标为交通流量真实值，纵坐标为DBN-SVR模型预测值。绿色散点横坐标为交通流量真实值，纵坐标为SVR模型预测值。从蓝色与绿色散点的分布情况看，蓝色散点较为聚合且与红色实线的重合度较高，而绿色散点较为离散且随着交通流量值的增大与红色实线偏离的程度越大，这说明DBN-SVR模型能较好地捕捉各个时刻交通流波动的状态，而SVR模型在交通高峰时刻的预测性能不如其他时间稳定。

第五章 基于多特性组合优化的短时交通流预测模型

5.1 多特性组合优化模型框架

基于短时交通流量的在工作日与非工作日的差异性、时间邻近性与空间关联性、受天气因素展现的随机性。本章提出了多特性组合优化的短时交通流预测模型，将前两章中两种模型在工作日与非工日下的交通流量预测结果，分别通过固定权重的信息熵加权组合算法和自适应调整权重的最小二乘动态加权组合算法进行组合优化，最后对两种组合优化模型的预测误差进行了比较分析。

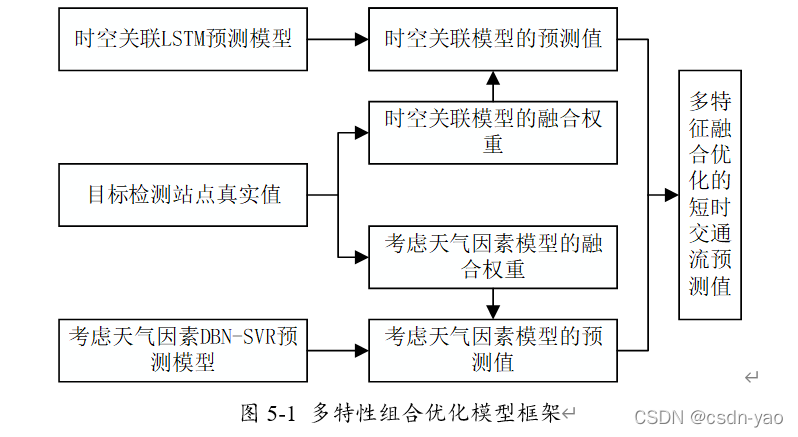
5.1 两种组合方式下的交通流预测误差分析

为了对比分析本章两种组合方法和上两章两种仅考虑交通流某种特性的单一预测模型的预测性能，将上两章两种单一预测模型与本章两种组合模型，共计4种预测模型在工作日下的预测误差置于图5-2中，同样的将非工作日下的预测误差置于图5-3中，图5-2与5-3中蓝色实线的长短表示预测误差。


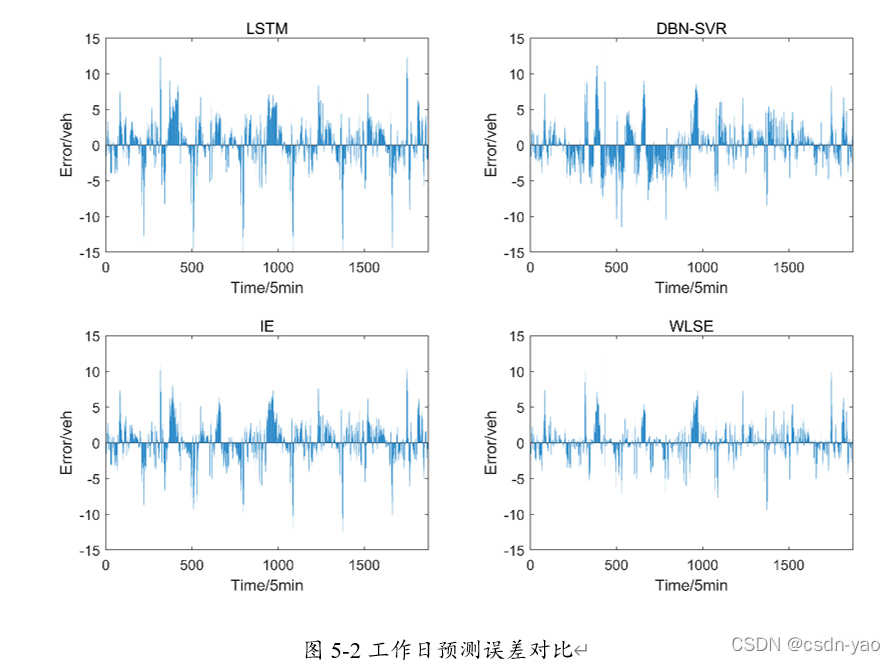
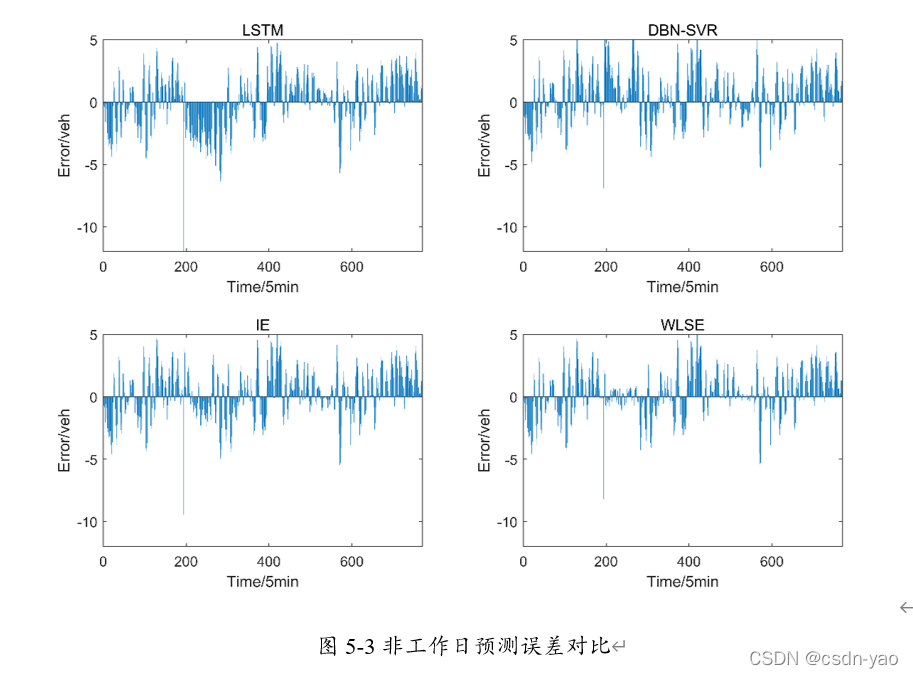
从图5-2与5-3工作日与非工作日下4种模型的预测误差可以看出，本章IE加权组合与WLSE组合的交通流预测误差相比于时空关联LSTM与引入天气因素的DBN-SVR模型的预测误差明显更小。其中WLSE组合方法的交通流预测误差最小同时波动也较小，这表明模型具有稳定性。时空关联LSTM与引入天气因素的DBN-SVR模型的预测误差存在较多突变点，不同时刻预测效果差异较大，这说明模型缺乏稳定性。这种不稳定性将直接影响交通诱导系统的实施效果。

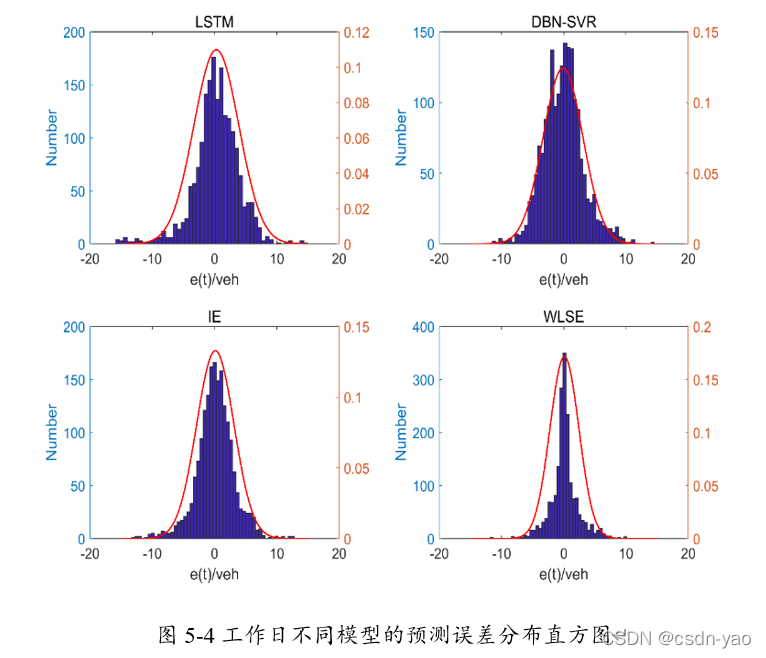
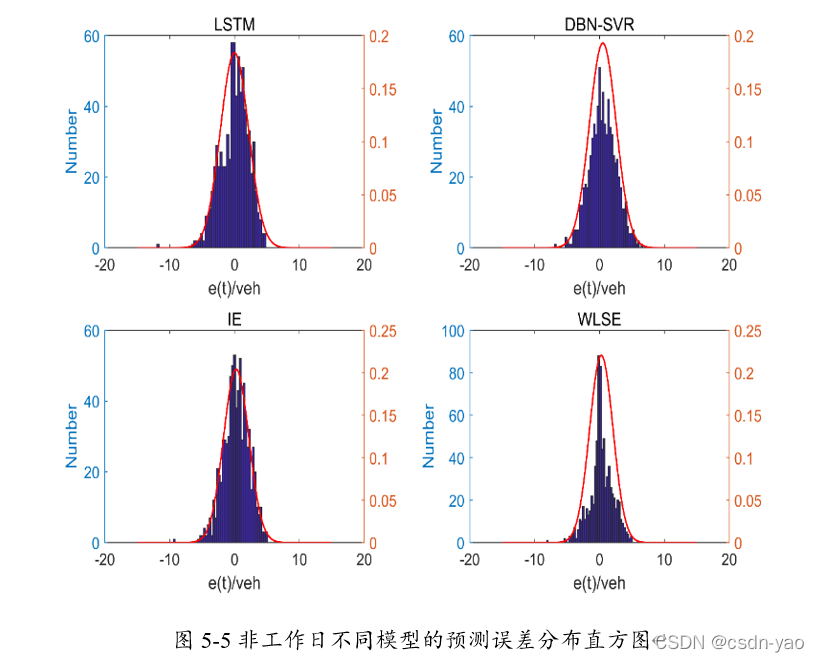
综上所述，组合预测模型的预测精度并不能每时每刻都比单一预测模型好，只有在单一预测模型的预测误差同时分布在正负两侧的情况下，相对于单一模型，组合模型的预测精度将会大大提高；在单一预测模型的预测误差同时分布在同一侧的情况下，组合模型不能抵消预测误差，最终组合结果不够理想。
因此在选择单项预测模型时，尽量选择在某些方面可以形成互补的模型，使得每种模型提供不同的信息以达到组合优化的目的[69]。正如本文分别从交通流内部机制决定的时间邻近性、空间关联性和外部因素影响的工作日与非工日的差异性、受天气因素影响的随机性多个不同方面入手，从而实现了不同信息的有效组合，获得了准确且稳定的交通流预测值。

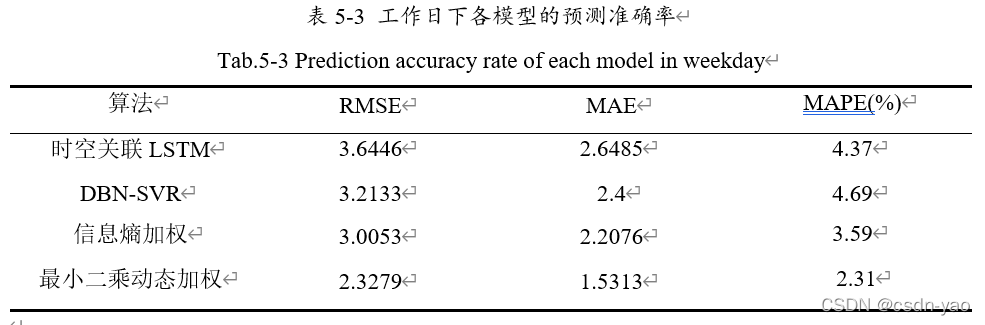
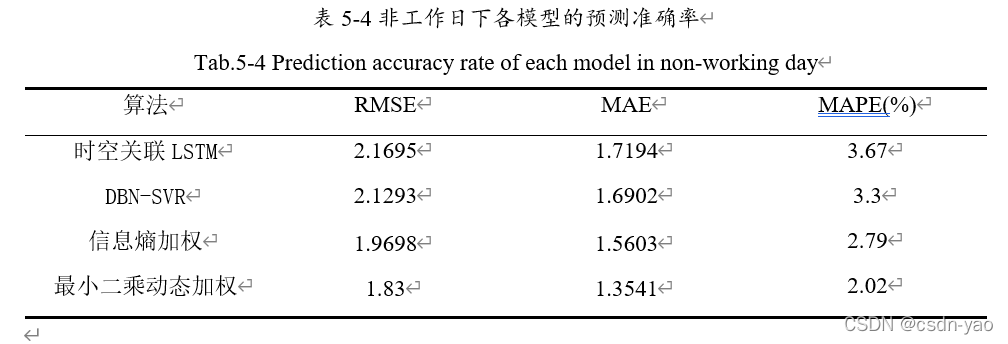
表5-3中给出工作日下时空关联LSTM、DBN-SVR、基于IE加权组合、基于WLSE组合，共计4种模型的交通流量预测结果的RMSE、MAE、MAPE值，从表5-3中可以得出结论：1、DBN-SVR模型的RMSE、MAE均小于LSTM模型，但是MAPE却大于LSTM，正如第二章2.5小节提到，时间序列预测模型预测结果的有效性，不能简单的使用一个指标来衡量，需要综合考虑多个指标。2、基于IE组合、基于WLSE组合的交通流量预测结果的三个评估指标上均比LSTM、DBN-SVR算法低，即多特性组合模型在性能上比单个模型好。3、基于WLSE组合的预测效果比基于IE加权组合的预测效果更好。