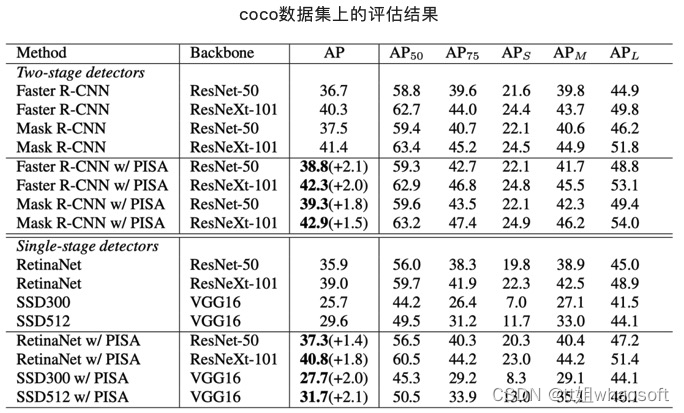
Prime算法
算法介绍:
课本实现方法:
先从最小堆说起(heap):任一结点的关键码均小于或等于它的左右子女的关键码,位于堆顶(即完全二叉树的根结点的位置)的结点的关键码是整个集合中最小的,称其为最小堆。
如果有关键码(各个数据记录中存在一个能够标识数据记录的数据项,并将其组织)的集合K={k0,k1,k2,...,kn-1},把它的所有元素按照完全二叉树的顺序存储来存放在一个一维数组中,满足ki≤k2i+1且ki≤k2i+2 ,
i=0,1,...[(n-2)/2],则称这个集合为最小堆。
通过在一个最小堆存储图的边,每次选出一个端点在生成树中,另一个端点不在生成树中的权值最小的边(u,v),另外一个正好在最小堆的堆顶,将其从堆中退出,加入生成树;然后将刚才新出的两个端点放置入最小堆中。
迭代,将权值最小的又上升到最小堆的堆顶。重复N-1次,建立该图的最小生成树。
代码见数据结构(清华大学系列教材)课本P375。
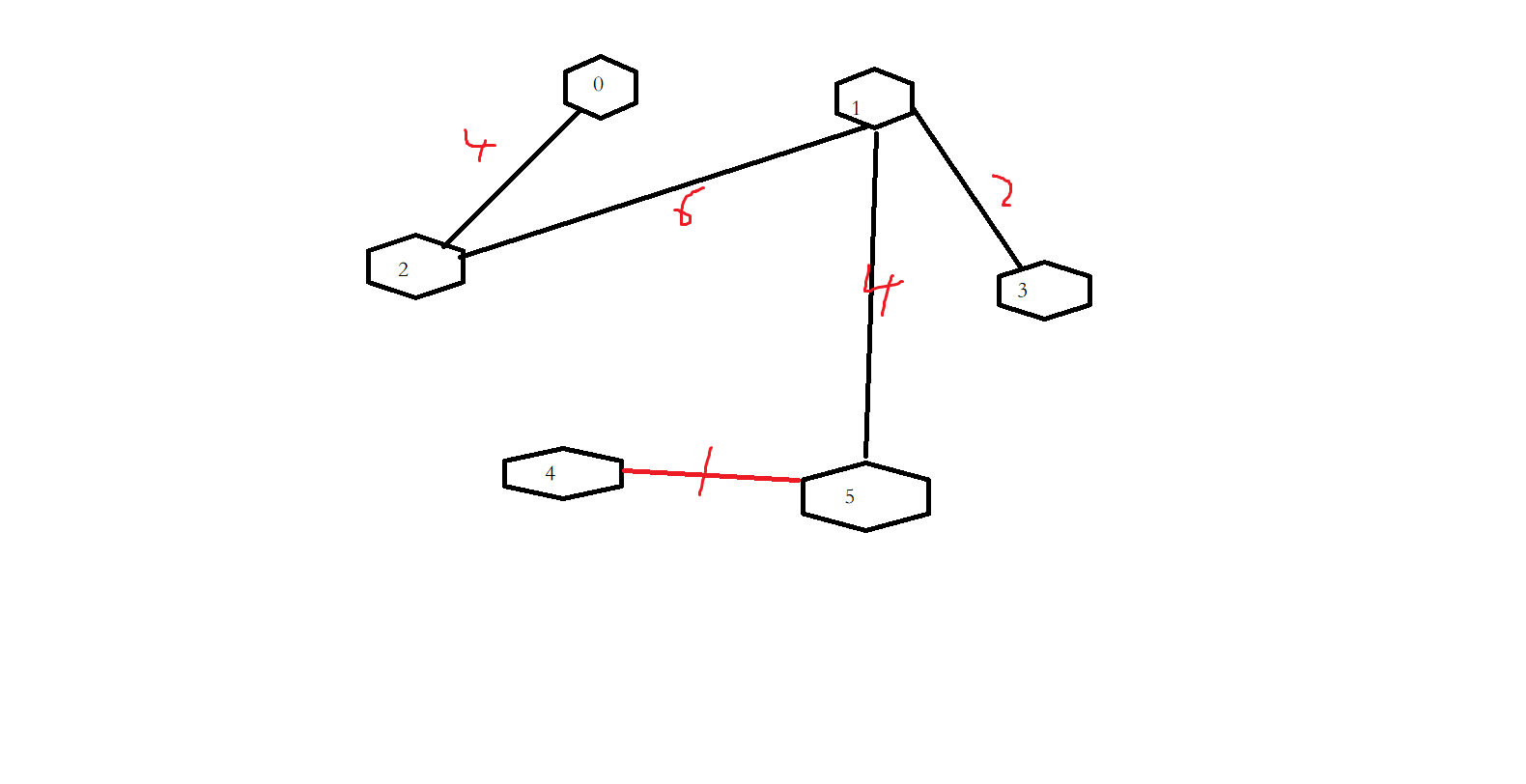
另外自己构造一个图,对其遍历求解最小生成树:
见图:
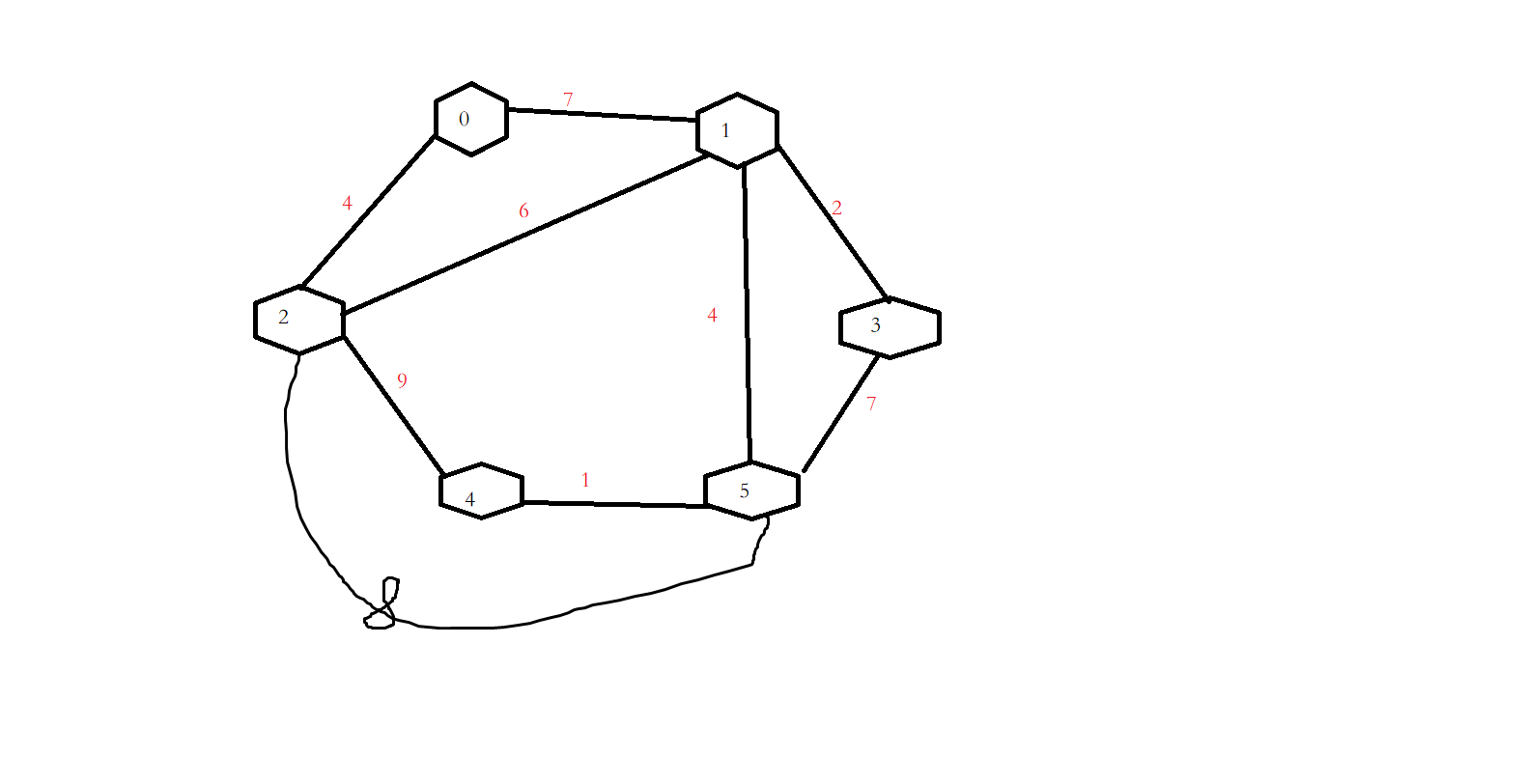
由上述图,得出最小生成树,
核心算法:
将该树分为两个集合A、B,A集合是最小生成树中的结点,B是未处理的结点,选择一个结点,将这个结点加入A中,然后,对集合A中的顶点遍历,找出A中顶点关联的边权值最小的顶点,将其从B中删除,加入集合A中,不断递归直至B中结点为空结 束。
关键:每在最小生成树集合中加入一个点就需要把这个点与集合外的点比较,不断的寻找两个集合之间最小的边。
例如上述图中,假设从0开始找最小生成树,遍历到1结点时,选择3结点,3结点为新加入的结点,将3结点加入到生成树集合中后,需要与集合外5结点相连的结点之间的权值比较,发现1结点与5结点的权值为4,3结点与5结点权值为7,因此,选择从1 结点到5结点的路径,加入最小生成树,直至所有点加入到生成树中,记录路径,统计长度。
因此,需要一个辅助数组visit[]记录是否加入最小生成树,还需要一个lowcost[]数组存放最小生成树,需要根据已经建立map[]数组(即邻接矩阵)来存储图的数据权值。对map的操作在关键处需要重新进行一个if判断(即判断!vist[j]=1&&lowcost[j]>map[index][j])lowcost[j]=map[index][j]; 也就是说map[index][j]图中的结点从index->j的权值小于最小生成树中lowcost[j]中已经进入结点的权值,就更新将map[index][j]更新值存到最小生成树的数组中。
代码如下:
1 #include<iostream> 2 #include<cstring> 3 #define INF 0x3f3f3f3f 4 using namespace std; 5 const int N = 6; 6 bool visit[N]; 7 int lowcost[N] = { 0 }; 8 int map[N][N] = { {INF,7,4,INF,INF,INF}, 9 {7,INF,6,2,INF,4}, 10 {4,6,INF,INF,9,8}, 11 {INF,2,INF,INF,INF,7}, 12 {INF,INF,9,INF,INF,1}, 13 {INF,4,8,7,1,INF} 14 }; 15 int prim(int cur) 16 { 17 int index = cur; 18 int sum = 0; //最短路径长 19 int i = 0 , j = 0; 20 cout << index << "->"; 21 memset(visit,false, sizeof(visit)); 22 visit[cur] = true; 23 for(i = 0; i < N; i++) 24 lowcost[i] = map[cur][i];//初始化,将cur结点所有相连的边放入 25 26 for(i = 1; i < N; i++)//两重for循环 遍历每一个结点 27 { 28 int min= INF; //定义一个变量min初始化为一个极大值 29 //第一个for循环 未访问的点与与索引点index的比较 30 for(j = 0; j < N; j++) 31 { 32 if(!visit[j] && lowcost[j] < min)//找到未访问的点中,距离当前最小生成树距离最小的点 33 { 34 min = lowcost[j]; //不断更新与点cur的相连点的最短距离,将lowcost[j]权值更新数据到min上 更新权值 35 index = j;//将j数组下标更新到index中(即cur)更新结点 36 } 37 } 38 visit[index] = true;//标记距离最短的结点已经被访问过 39 cout << index << "->";//输出新结点 40 sum += min;//权值累加 41 //第二个for循环 从index结点开始遍历的图中的新结点map[index][j]与最小生成树中lowcost[j]旧结点之间的权值遍历比较 42 for(j = 0; j < N; j++) 43 { 44 if(!visit[j] && lowcost[j]>map[index][j]) 45 { 46 lowcost[j] = map[index][j]; 47 } 48 } 49 } 50 cout << endl; 51 return sum; //返回最小生成树的总路径值 52 } 53 int main() 54 { 55 cout << prim(0) << endl;//从0开始 56 cout << prim(1) << endl;//从1开始 57 cout << prim(2) << endl;//从2开始 58 cout << prim(3) << endl;//从3开始 59 cout << prim(4) << endl;//从4开始 60 cout << prim(5) << endl;//从5开始 61 return 0; 62 } 63 64
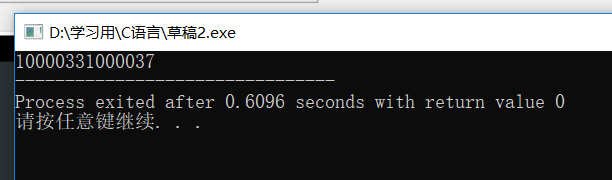
测试结果:
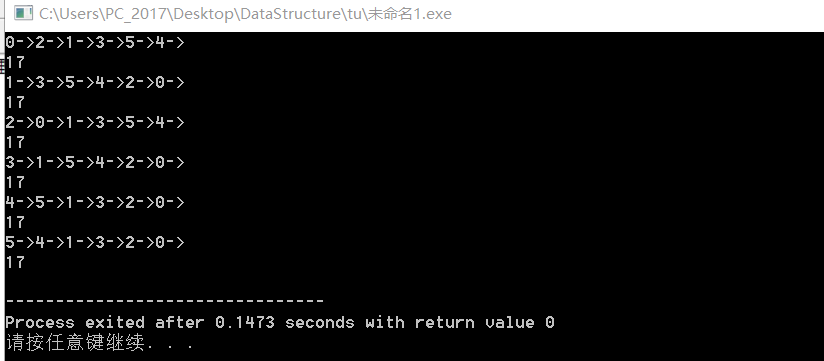
最终图为: