文章目录
- 1. 基本概念
- 1.1 自相关函数ACF(autocorrelation function)
- 1.2 偏自相关函数PACF(partial autocorrelation function)
- 2. 常见模型
- 2.1 自回归模型(AR)
- 2.2 移动平均模型(MA)
- 2.3 自回归移动平均模型(ARMA)
- 2.4 差分自回归移动平均模型(ARIMA)
- 4. 建模步骤
- 4.1 平稳性检验
- 4.1.1 时序图、自相关图、偏自相关图
- 4.1.2 自相关、偏自相关图
- 4.1.3 单位根检验
- 4.1.4 差分运算
- 4.2 白噪声检验
- 4.3 模型选择(p,q,d)
- 4.3.1 AIC与BIC
- 4.3.2 模型稳定性检验
- 4.4 模型预测
| 模型名称 | 描述 |
|---|---|
| 平滑法 | 削弱短期随机波动对序列的影响,序列插值分布均匀 |
| 趋势拟合法 | 把时间作为自变量,相应序列观察值作为因变量,简历回归模型 |
| 组合模型法 | 受长期趋势(T)、季节变动(S)、周期变动(C)和不规则变动(ε)四个因素影响 |
| 组合模型 | (1)加法模型: T + S + C + ϵ T+S+C+\epsilon T+S+C+ϵ (2)乘法模型: T S C ϵ T SC\epsilon TSCϵ |
常见时间序列模型
| 模型名称 | 描述 |
|---|---|
| AR模型 | 考虑历史数据的影响,以过往数据为自变量, X t X_t Xt为因变量建立线性回归模型。 X t = ϕ 0 + ϕ 1 x t − 1 + ⋯ + ϕ p x t − p X_t=\phi_0+\phi_1 x_{t-1}+\cdots+\phi_p x_{t-p} Xt=ϕ0+ϕ1xt−1+⋯+ϕpxt−p |
| MA模型 | 忽略历史数据影响,建立于前q期随机扰动 ϵ t − 1 , ⋯ , ϵ t − q \epsilon_{t-1},\cdots,\epsilon_{t-q} ϵt−1,⋯,ϵt−q的线性回归模型 X t = μ + ϵ t − θ 1 ϵ t − 1 − ⋯ − θ q ϵ t − q X_t=\mu+\epsilon_t-\theta_1 \epsilon_{t-1}-\cdots-\theta_q \epsilon_{t-q} Xt=μ+ϵt−θ1ϵt−1−⋯−θqϵt−q |
| ARMA模型 | 结合考虑AR、MA模型,综合考虑它们的影响 |
| ARIMA模型 | 针对非平稳序列。将非平稳转化为平稳后拟合操作 |
1. 基本概念
白噪声序列: 数据随机分布,没有规律。
平稳非白噪声序列
非平稳序列: 可以利用差分法转换为平稳非白噪声序列
截尾: 拖尾指序列以指数率单调递减或震荡衰减
拖尾: 截尾指序列从某个时点变得非常小

1.1 自相关函数ACF(autocorrelation function)
- 自相关函数反映了同一序列在不同时序的取值之间的相关性。
- 公式:
A C F ( k ) = ρ k = C o v ( y t , y t − k ) V a r ( y t ) ACF(k) = \rho_k=\frac{Cov(y_t,y_{t-k})}{Var(y_t)} ACF(k)=ρk=Var(yt)Cov(yt,yt−k)
其中, ρ k ∈ [ − 1 , 1 ] \rho_k \in[-1,1] ρk∈[−1,1]
1.2 偏自相关函数PACF(partial autocorrelation function)
- 剔除了中间k-1个随机变量 x ( t − 1 ) , x ( t − 2 ) , ⋯ , x ( t − k + 1 ) x(t-1),x(t-2),\cdots,x(t-k+1) x(t−1),x(t−2),⋯,x(t−k+1)的干扰后 x ( t − k ) x(t-k) x(t−k)对 x ( t ) x(t) x(t)影响的相关程度
- PACF是严格两个变量之间的相关性。
2. 常见模型
2.1 自回归模型(AR)
定义:
-
描述当前值与历史值之间的关系。利用历史数据对自身进行预测
-
P阶自回归过程,即当前值与 t − p , t − p + 1 , ⋯ , t − 1 t-p,t-p+1,\cdots,t-1 t−p,t−p+1,⋯,t−1相关(P)。
y t = μ + ∑ i = 1 p γ i y t − i + ϵ t y_t=\mu+\sum_{i=1}^{p} \gamma_i y_{t-i} + \epsilon_t yt=μ+i=1∑pγiyt−i+ϵt
其中, y t y_t yt是当前值, μ \mu μ是常数项,P是阶数, γ i \gamma_i γi是自相关系数, ϵ \epsilon ϵ是误差。 -
参数:P(自回归阶数)
注意
- 必须具有平稳性
- 必须具有自相关性,自相关系数需要大于等于0.5.
模型识别
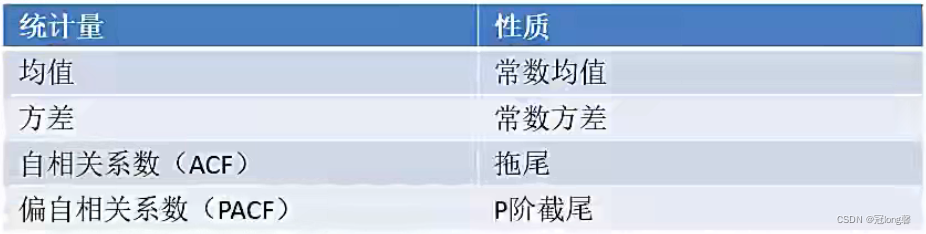
2.2 移动平均模型(MA)
定义
-
移动平均模型是自回归模型中误差项的累加
-
q阶移动模型公式(Q):
y t = μ + ϵ t + ∑ i = 1 q θ i ϵ t − i y_t = \mu + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i} yt=μ+ϵt+i=1∑qθiϵt−i -
移动平均法能有效地消除预测中的随机波动
-
参数:Q(移动平均阶数)
模型识别

2.3 自回归移动平均模型(ARMA)
定义
-
自回归与移动平均的结合
-
公式定义为(P,Q):
y t = μ + ∑ i = 1 p γ i y t − i + ϵ t + ∑ i = 1 q θ i ϵ t − i y_t = \mu + \sum_{i=1}^{p} \gamma_i y_{t-i} + \epsilon_t + \sum_{i=1}^{q} \theta_i \epsilon_{t-i} yt=μ+i=1∑pγiyt−i+ϵt+i=1∑qθiϵt−i -
参数:P(自回归阶数),Q(移动平均阶数)
模型识别
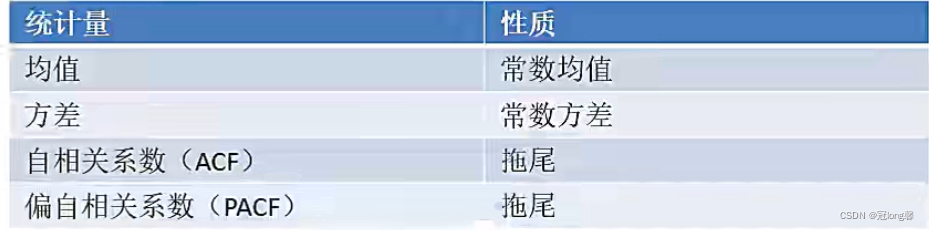
2.4 差分自回归移动平均模型(ARIMA)
对于ARIMA模型,我们需要指定三个参数(P, D, Q),分别表示P阶自回归模型,D阶差分和Q阶移动平均模型。
定义:
- 参数:(P, D, Q),分别表示P阶自回归模型,D阶差分和Q阶移动平均模型。
- 原理:将非平稳时间序列转换为平稳时间序列,然后将因变量对其滞后值和其随机误差的滞后值进行回归建模。
4. 建模步骤
4.1 平稳性检验
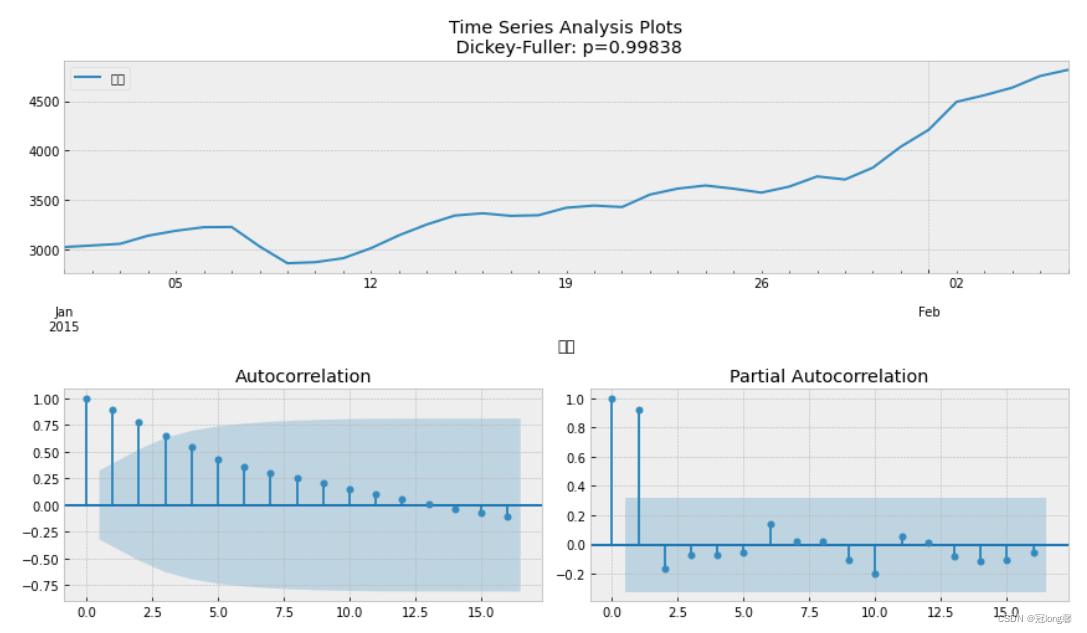
4.1.1 时序图、自相关图、偏自相关图
def tsplot(y,lags=None,figsize=(12,7),style='bmh'):'''Plot time series, its ACF and PACF, calculate Dickey-Fuller testy:timeserieslags:how many lags to include in ACF,PACF calculation'''
# if not isinstance(y, pd.Series):
# y = pd.Series(y)with plt.style.context(style):fig = plt.figure(figsize=figsize)layout=(2,2)ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)acf_ax = plt.subplot2grid(layout, (1,0))pacf_ax = plt.subplot2grid(layout, (1,1))y.plot(ax=ts_ax)p_value = sm.tsa.stattools.adfuller(y)[1]ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value))smt.graphics.plot_acf(y,lags=lags, ax=acf_ax)smt.graphics.plot_pacf(y,lags=lags, ax=pacf_ax)plt.tight_layout()
tsplot(data)
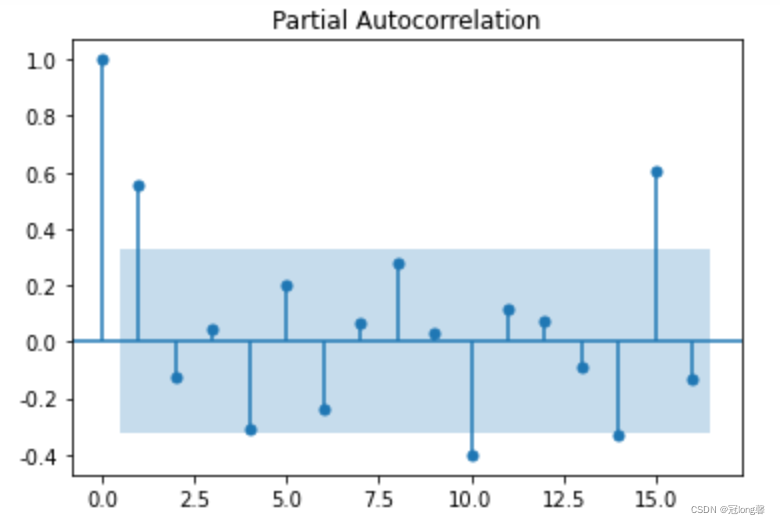
4.1.2 自相关、偏自相关图
根据自相关图,判断“拖尾”、“截尾”。
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()
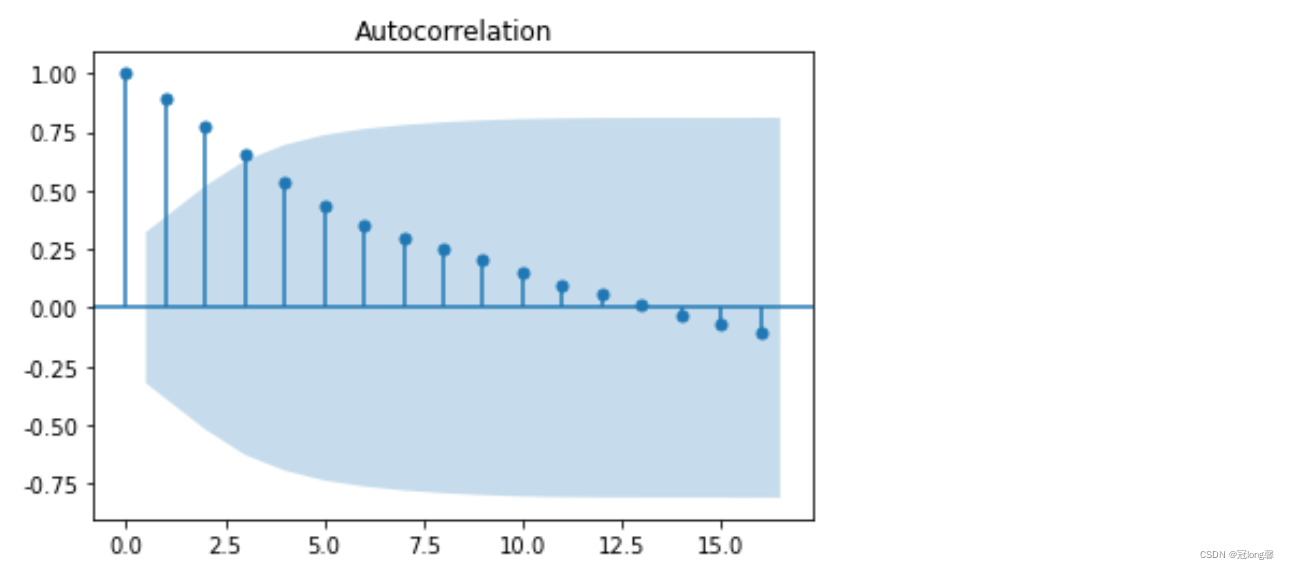
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data).show()
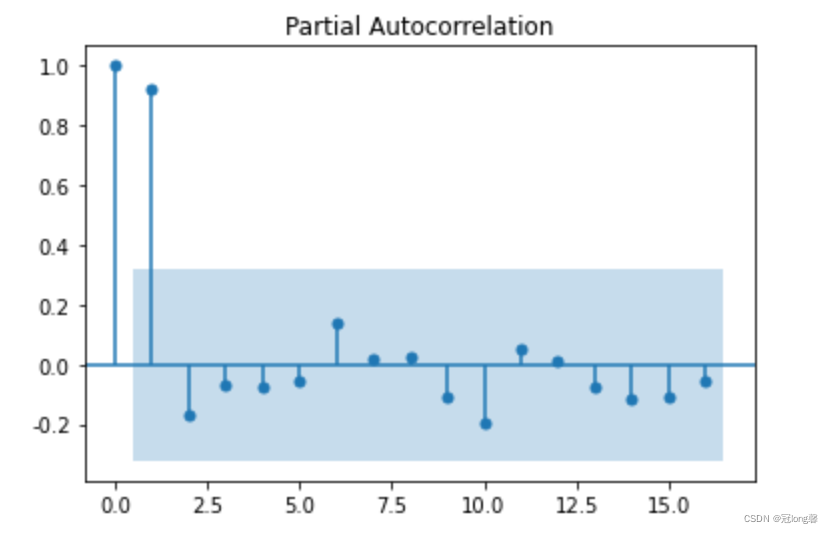
4.1.3 单位根检验
采用单位根法检验,当单位根大于等于0.05时,表示数据为非平稳序列。
from statsmodels.tsa.stattools import adfuller as ADF
print('原始序列数据的ADF检测结果为:')
print(ADF(data['销量']))
# 返回值依次为: adf, pvalue(单位根,>=0.05就是非平稳序列)
原始序列数据的ADF检测结果为:
(1.813771015094526, 0.9983759421514264, 10, 26, {‘1%’: -3.7112123008648155, ‘5%’: -2.981246804733728, ‘10%’: -2.6300945562130176}, 299.4698986602418)
4.1.4 差分运算
若序列为非平稳序列,则需要转换为平稳序列计算
(1)差分运算
- P阶差分
相距一期的两个序列之间的减法运算称为1阶差分运算
将1阶差分运算的结果再做一次差分运算则称为2阶差分运算 - K步差分
相距k期的两个序列值之间的减法运算称为k步差分运算
1. 差分运算
D_data = data.diff().dropna() # 一阶一步差分,并去除NA
D_data.columns = ['sale diff']
2. 差分结果检验
对差分结果进行相同的平稳性检验,当单位根值小于等于0.05时,表示已经转换为平稳序列。
# 自相关图
plot_acf(D_data).show()
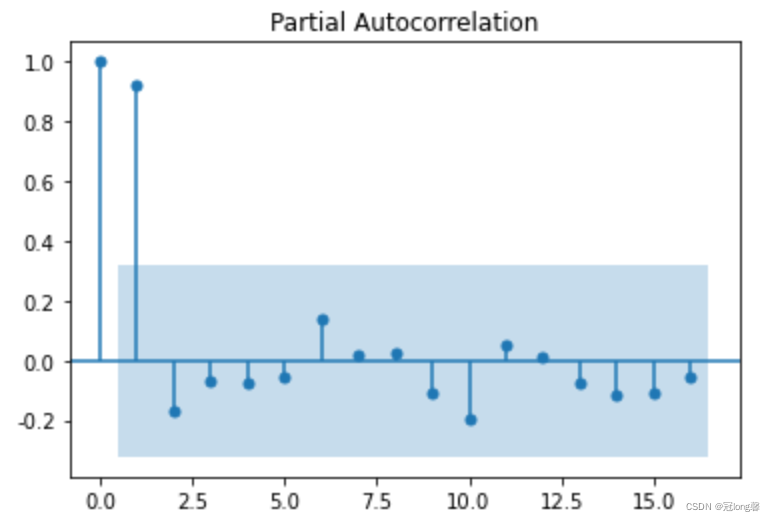
# 偏自相关图
plot_pacf(D_data).show()
# 单位根值
print('原始序列数据进行一次一步差分的ADF检测结果为:')
print(ADF(D_data['sale diff']))
原始序列数据进行一次一步差分的ADF检测结果为:
(-3.1560562366723537, 0.022673435440048798, 0, 35, {‘1%’: -3.6327426647230316, ‘5%’: -2.9485102040816327, ‘10%’: -2.6130173469387756}, 287.5909090780334)
4.2 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print('差分序列的白噪声检验结果:')
print(acorr_ljungbox(D_data,lags=1)) # 返回统计量与p值,当p <= 0.05 时,不是白噪音
差分序列的白噪声检验结果:
(array([11.30402222]), array([0.00077339]))
4.3 模型选择(p,q,d)
AR, MA模型
通过ACF, PACF截尾开始阶数确定p, q参数值。
- AR§:PACF上截尾,ACF趋近于0
- MA(Q):ACF上截尾,PACF趋近于0
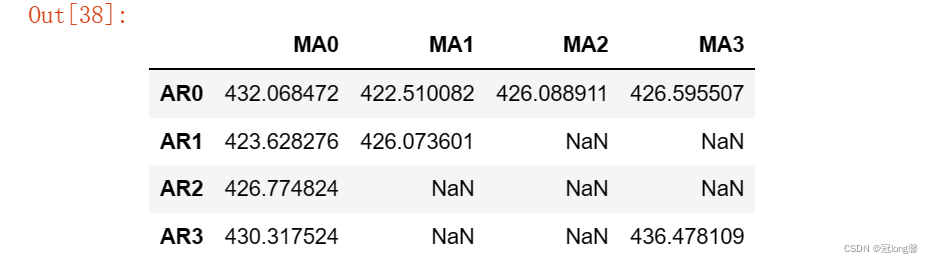
采用BIC矩阵,找到最小值对应的p, q值。并以此为参数选择下述三个模型:

4.3.1 AIC与BIC
AIC:赤池信息准则(Akaike information Criterion)
A I C = 2 k − 2 ln ( L ) AIC = 2k-2\ln(L) AIC=2k−2ln(L)
BIC:贝叶斯信息准则(Bayesian information Criterion)
B I C = k ln ( n ) − 2 ln ( L ) BIC = k\ln(n)-2\ln(L) BIC=kln(n)−2ln(L)
其中,k为模型参数个数,n为样本数量,L为似然函数。
- AIC, BIC值越低越好
- 希望通过AIC, BIC选择更简单的模型,P, Q越大,所需参数项数目越多。
from statsmodels.tsa.arima_model import ARIMA
# 定阶
# data['销量']=data['销量'].astype(float)
pmax = int(len(D_data)/10)
qmax = int(len(D_data)/10)bic_matrix = [] # BIC矩阵
for p in range(pmax+1):tmp = []for q in range(qmax+1):try: # 部分报错,跳过tmp.append(ARIMA(data,(p,1,q)).fit().bic)except:tmp.append(None)bic_matrix.append(tmp)bic_matrix = pd.DataFrame(bic_matrix)
bic_matrix.index = ['AR{}'.format(i) for i in range(pmax+1)]
bic_matrix.columns = ['MA{}'.format(i) for i in range(qmax+1)]
bic_matrix = bic_matrix[bic_matrix.columns].astype(float)p,q = bic_matrix.stack().idxmin()
print('最小BIC对应的p,q值:%s, %s'%(p,q))
最小BIC对应的p,q值:0, 1
import seaborn as sns
fig, ax = plt.subplots(figsize = (10,8))
ax = sns.heatmap(bic_matrix,mask = bic_matrix.isnull(),ax = ax,annot = True,fmt='.2f')
ax.set_title('BIC')
result = smt.arma_order_select_ic(data, ic=['aic', 'bic'], trend='nc', max_ar=4, max_ma=4)
{‘aic’: 0 1 2 3 4
0 NaN 668.212060 627.212365 590.498371 565.724666
1 472.121781 442.706792 444.414985 441.613728 442.640421
2 449.878586 443.006993 445.873538 443.364868 445.454087
3 452.992514 441.894814 443.613869 449.670033 442.185777
4 454.442210 443.477934 445.326246 445.745273 445.296295,
‘bic’: 0 1 2 3 4
0 NaN 671.433896 632.045119 596.942043 573.779256
1 475.343616 447.539546 450.858657 449.668317 452.305928
2 454.711339 449.450664 453.928128 453.030375 456.730513
3 459.436186 449.949403 453.279376 460.946459 455.073120
4 462.496800 453.143442 456.602672 458.632617 459.794557,
‘aic_min_order’: (1, 3),
‘bic_min_order’: (1, 1)}
由此可以选择MA模型,或者p =0, q =1的ARMA模型。可以将做完差分的数据带入平稳模型或者将原数据带入非平稳模型,并设置阶数。
4.3.2 模型稳定性检验
模型残差检验
- ARIMA的残差是否是平均值为0且方差为常数的正太分布
- QQ图:线性即正太分布
4.4 模型预测
model = ARIMA(data, (p,1,q)).fit()
print('模型报告为:\n', model.summary2())
print('未来5天的预测结果、准确误差及置信区间:\n',model.forecast(5))