一、实验目的

1. 理解常见图像增强方法的原理和特点；

2. 掌握常见的灰度线性和非线性变换方法；

3. 掌握直方图均衡增强的原理与应用方法；

4. 掌握模板卷积的概念、原理与实现方法

5. 掌握均值滤波的技术原理与实现方法；

6. 掌握中值滤波的技术原理与实现方法；

二、实验内容

1. 图像的灰度线性变换

2. 图像的灰度非线性变换

三、实验步骤

1. 图像的灰度线性变换

2. 图像的灰度非线性变换

3. 直方图均衡化方法的应用

4. 图像均值滤波方法的应用

5. 图像中值滤波方法的应用

实验工具：matlabR2021b

一、实验目的

1. 理解常见图像增强方法的原理和特点；

2. 掌握常见的灰度线性和非线性变换方法；

3. 掌握直方图均衡增强的原理与应用方法；

4. 掌握模板卷积的概念、原理与实现方法

5. 掌握均值滤波的技术原理与实现方法；

6. 掌握中值滤波的技术原理与实现方法；

二、实验内容

1. 图像的灰度线性变换

（1）给定2 幅图像（raising_moon.jpg 和 CTimag.png)，要求通过线性变换方法实现

其对比度增强（如下图所示）。

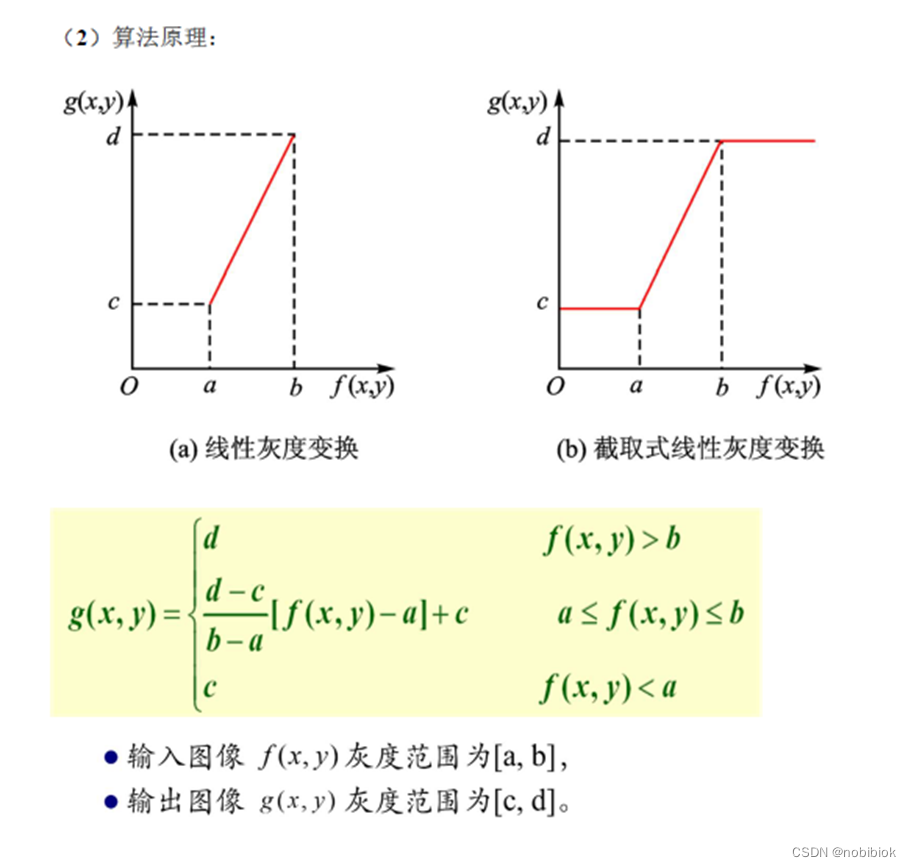
2. 图像的灰度非线性变换

（1）给定1 幅图像(GThxh.png)，要求通过对数变换实现其对比度增强（如下图）。

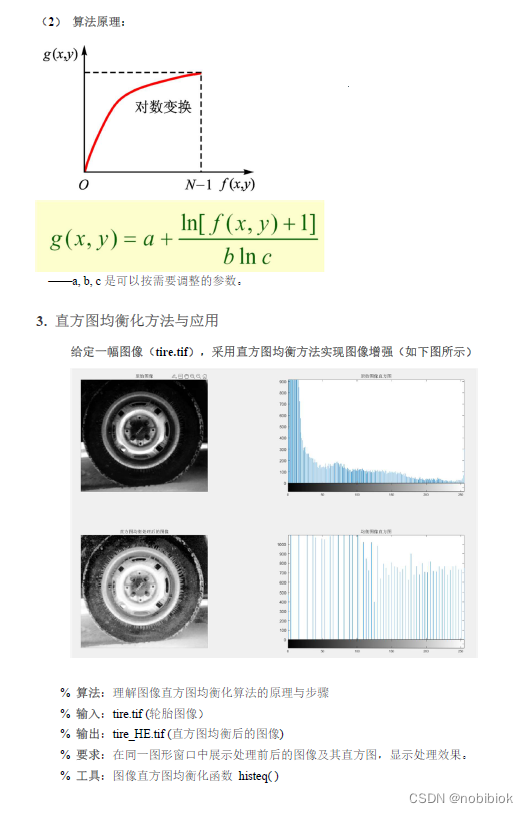
三、实验步骤

1. 图像的灰度线性变换

I=imread('raising_moon.jpg');
I1=double(I);% I 转换为I1 的目的是精度问题，因为uint8进行数据处理的时候，容易造成数据溢出或精度不够
I2=I;
J=I1*255/60;%公式为：g（x，y）=[（（255-0）/（60-0）]*f(x,y)+0
J2=I2*255/60;
K=uint8(J); % 增强后的图像数据
figure, subplot(321), imshow(I); title('原始图像（8 bits）');
subplot(322), imhist(I); title('原始图像直方图');% 发现像素灰度主要集中在[0 60]之间，是造成图像整体灰暗的原因
subplot(323), imshow(K); title('灰度线性增强图像');
subplot(324), imhist(K); title('增强图像直方图');
subplot(325), imshow(J2); title('没有double图像');
subplot(326), imhist(J2); title('没有double图像直方图');

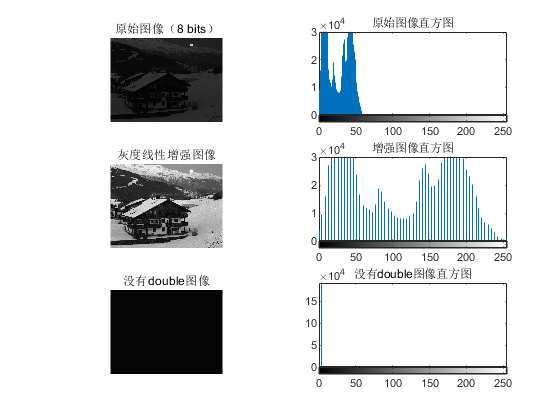
【思考与练习】

① 在灰度变换算法编程时，为什么要进行图像数据类型的转换？如何转换？

答：因为灰度图像数据类型是无符号八位数据，如果直接进行计算，会导致数据丢失，达不到想要的效果。转换方法可以是：I1=double(I)

② 如果直接使用图像数据类型进行图像数据的算法处理会带来什么问题？

答：在这张图像中这样处理会导致处理后的图像直方图灰度集中在0附近，如“没有double图像直方图”所示。

③ 试采用 for 循环和直接使用矩阵运算两种编程方式，实现同一图像数据处理过程（譬如，上述的灰度增强处理）。

1.for 循环

t0=cputime;
I=imread('raising_moon.jpg');
figure,subplot(221),imshow(I),title('原图像');
[m,n]=size(I);
Io=zeros(m,n);
I1=double(I);
for i=1:m
for j=1:n
Io(i,j)=255*I1(i,j)/60;
end
end
K=uint8(Io);
subplot(222),imhist(I),title('原图像直方图');
subplot(222),imhist(I),title('原图像直方图');
subplot(223),imshow(K),title('for图像');
subplot(224),imhist(K),title('for图像直方图');
t1=cputime-t0

t1 = 0.8750

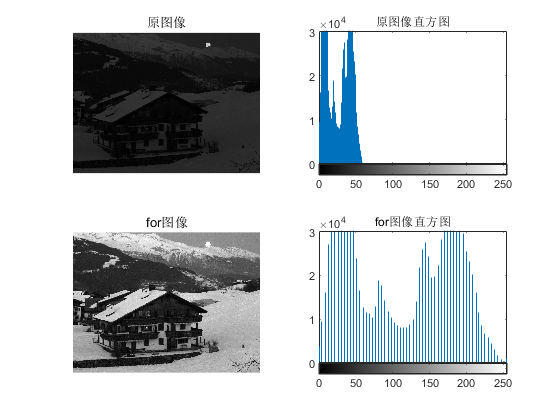
2.矩阵运算

t0=cputime;
I = imread('raising_moon.jpg');
I1 = double(I);
J = I1 * 255 / 60;
K = uint8(J);
figure, subplot(2, 2, 1), imshow(I), title('原始图像(8 bits)');
subplot(2, 2, 2), imhist(I), title('原始图像直方图');
subplot(2, 2, 3), imshow(K), title('灰度线性增强图像');
subplot(2, 2, 4), imhist(K), title('增强图像直方图');
t1=cputime-t0

t1 = 0.4375

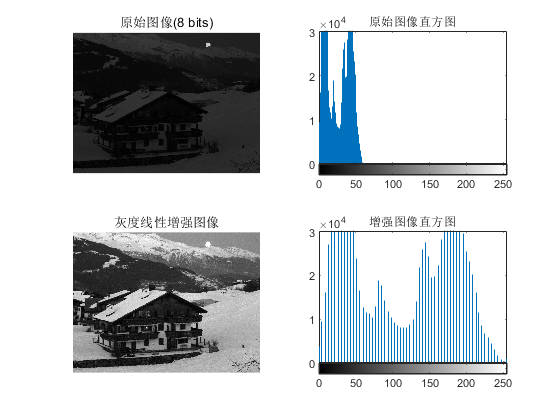
④ 比较两种方式所耗时间有无差异，体会MATLAB 矩阵运算的优势和特点。

答：矩阵运算比使用for循环速度更快。使用矩阵运算时，Matlab 可以直接对整个图像矩阵进行运算，从而提高了计算效率，进而缩小运算时间。

⑤ 试采用相同的原理和编程方法，实现医学图像“CTimag.png”的灰度线性增强；并对

比显示增强前后的图像。

I = imread('CTimag.png');
I1 = double(I);
J = I1 * 255 / 4000;%J=I1 * 65536/ 4000;
%J=J/256;
K = uint8(J);
figure, subplot(2, 2, 1), imshow(I), title('原始图像(8 bits)');
subplot(2, 2, 2), imhist(I), title('原始图像直方图');
subplot(2, 2, 3), imshow(K), title('灰度线性增强图像');
subplot(2, 2, 4), imhist(K), title('增强图像直方图');

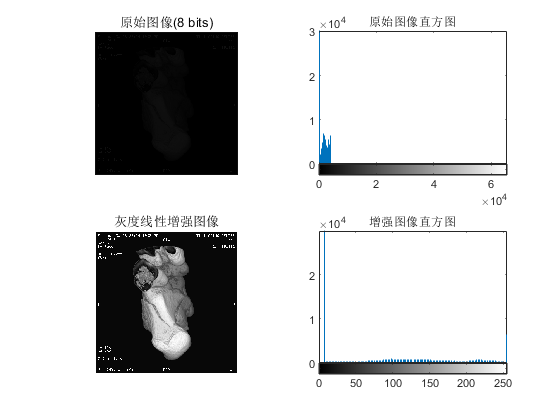
对比两图像，处理后的更易于观察。

2. 图像的灰度非线性变换

I=imread('GThxh.png');
A=rgb2gray(I); % 转化成灰度图像
figure,subplot(221),imshow(A),title('yuan');
subplot(222),imhist(A),title('yuan'); % 显示图像直方图
f=1:255; % 设置变换区间
a=50,b=0.03,c=2.5; % 设置变换系数
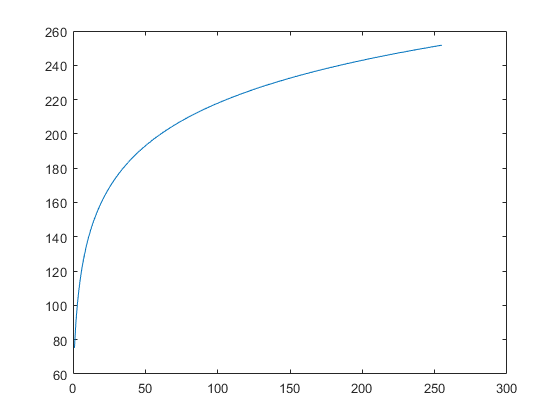
g=a+log(f+1)/(b*log(c)); % 计算对数变换
B=a+log(double(A)+1)/(b*log(c)); % 为什么要将A 转换成double 类型
C=uint8(B);
subplot(223),imshow(C),title('log'); % 显示图像A 的非线性增强效果
subplot(224),imhist(C),title('log'); % 绘制增强后的直方图
figure,plot(f,g); % 绘制变换曲线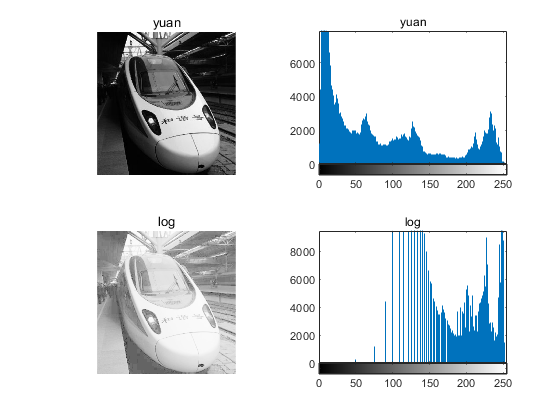

【思考与练习】

① 图像A 的数据类型是什么？在做对数变换时，为什么要将A 转换成double 类型？

答：无符号8位。因为不转换成double类型会数据溢出。

② 参照上述线性变换的第(4)步，在同一个图形窗口中对比展示图像A 的非线性增强效果。

答：如上所示，经过非线性增强后能看见图像暗处有人等细节。

③ 根据图像增强的效果，试分析图像对数变换处理的优势和问题。

答：

一、优势：处理后，直方图分布更均匀，图像更利于人眼观察；增强了低灰度区域的细节，压缩高灰度区域对比度。

二、问题：处理过程复杂，需要确定参数（abc）合适的值，才能达到想要的效果；易受噪声影响，对数变换容易受到图像噪声的影响，因为它会放大低灰度像素的细节，而这些低灰度像素往往是噪声所在的区域；计算机计算量较大。

④ 根据图像增强理论和方法，是否能够对给定的“和谐号”图像做到“低展”+“高平”处理？

——即对较低灰度范围内的像素值进行“扩展或拉伸”，而对灰度较高范围内的像素值保持

不变，以消除对数变换处理的负作用。

答：可以的。可以使用幂运算，近乎低灰度拉伸，高灰度保持。也可以使用for加if对图像进行处理。

⑤ 如果可以，请给出相应的算法，并编程测试。

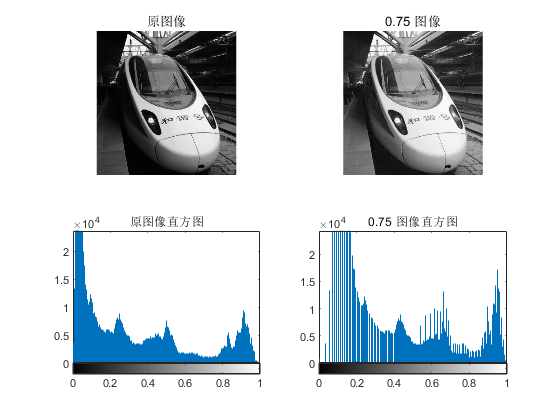
G=imread('GThxh.png');%读取图像
G1=im2double(G);
G2=G1.^(0.6);
figure,subplot(221),imshow(G1);title('原图像');
subplot(222),imshow(G2);title('0.75 图像');
subplot(223),imhist(G1);title('原图像直方图');
subplot(224),imhist(G2);title('0.75 图像直方图');

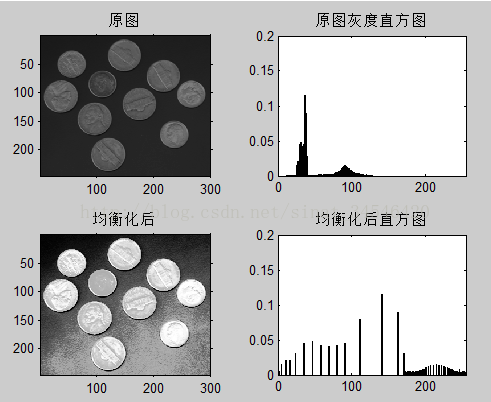
3. 直方图均衡化方法的应用

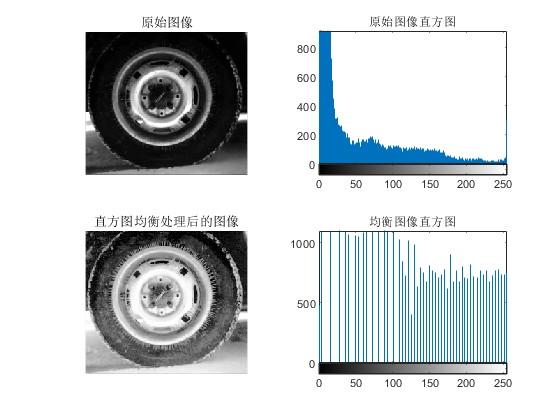
T=imread('tire.tif');
H=histeq(T);
imwrite(H,'tire_HE.tif');
figure, subplot(221),imshow(T),title('原始图像')
subplot(222),imhist(T),title('原始图像直方图');
subplot(223),imshow(H),title('直方图均衡处理后的图像');
subplot(224),imhist(H),title('均衡图像直方图');

【思考与练习】

① 图像直方图均衡化的原理是什么？

答：通过累积分布函数变成近似均匀分布，增强图像的对比度。

② 直方图均衡化的变换函数是什么？

答：累积分布函数。

③ 直方图均衡化算法的实现步骤有哪些？

答：

1依次扫描原始灰度图像的每一个像素，计算出图像的灰度直方图。

2计算灰度直方图的累积分布函数。

3根据累积分布函数和直方图均衡化原理得到输入与输出之间的映射关系。

4最后根据映射关系得到结果进行图像变换.

④ 试编写一个直方图均衡化程序，并测试分析。

答：

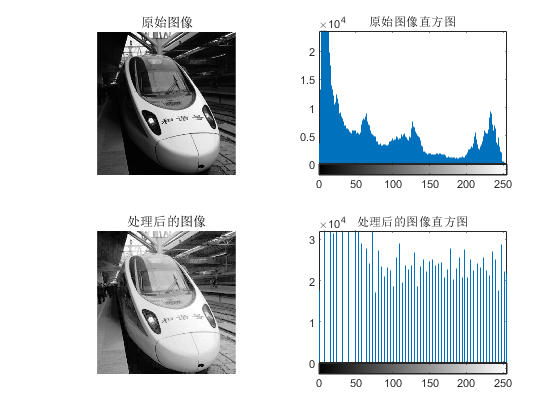
E=imread('GThxh.png');
F=histeq(E);
figure, subplot(221),imshow(E),title('原始图像');
subplot(222),imhist(E),title('原始图像直方图');
subplot(223),imshow(F),title('处理后的图像');
subplot(224),imhist(F),title('处理后的图像直方图');

4. 图像均值滤波方法的应用

I=imread('coins.png');
Ig=imnoise(I,'gaussian',0.1,0.004); % 给图像加入均值为0.1、方差为0.004 的高斯噪声
figure, subplot(121),imshow(I); title('原始图像');
subplot(122),imshow(Ig);title('加噪图像');

h=ones(3,3)/9; % 设置平滑模板（卷积核）
Is=imfilter(Ig,h); % 平滑滤波运算
imwrite(Is, 'coins_smt.jpg'); % 平滑滤波后图像的输出保存
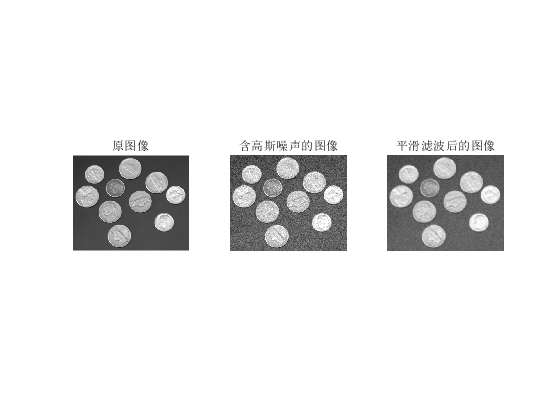
figure, subplot(131),imshow(I);title('原图像');
subplot(132),imshow(Ig),title('含高斯噪声的图像');
subplot(133),imshow(Is),title('平滑滤波后的图像');

【思考与练习】

① 图像均值平滑滤波的原理是什么？

答：其基本原理是图像像素点的值处理为邻域内其他像素点的均值。

② 写出上述滤波程序所采用的卷积算法公式。

答：卷积运算就是对于图像f(x,y) 中的每个像素，将其作为中心像素，计算它及其邻域像素和kernel

核w(a,b)对应位置元素的乘积，然后把结果相加到一起，得到的值就作为该中心像素的新值，这样就

完成了一次卷积运算。然后将kernel 向下或向左平移一位继续计算每个像素的新值，直到遍历完整个

图像。

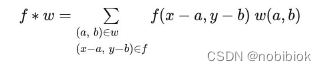
③ 通过帮助系统，了解 imnoise( ) 和 imfilter() 函数的详细用法。

答：

J = imnoise(I,'gaussian') 将方差为 0.01 的零均值高斯白噪声添加到灰度图像 I。

J = imnoise(I,'gaussian',m) 添加高斯白噪声，均值为 m，方差为 0.01。

B = imfilter(A,h) 使用多维滤波器 h 对多维数组 A 进行滤波，并在 B 中返回结果。

B = imfilter(A,h,options,...) 根据一个或多个指定的选项执行多维滤波

5. 图像中值滤波方法的应用

I=imread('eight.tif');
J=imnoise(I,'salt & pepper',0.03); % 给原始图像加入椒盐噪声（黑白点概率均为0.03）
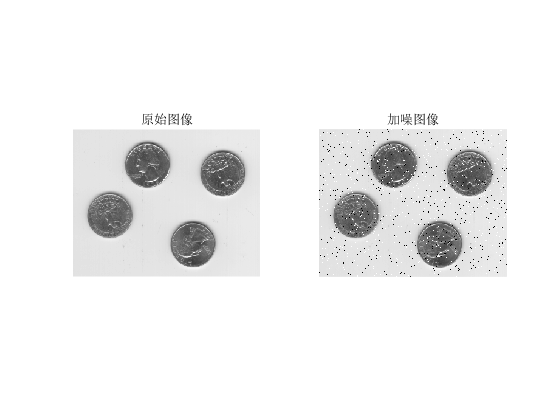
figure, subplot(121),imshow(I); title('原始图像');
subplot(122),imshow(J);title('加噪图像');

K=medfilt2(J); % 中值滤波
imwrite(K, 'eight_smt.jpg'); % 滤波图像保存
figure,subplot(131),imshow(I);title('原图像');
subplot(132), imshow(J), title('椒盐噪声加入原图像');
subplot(133), imshow(K), title('中值滤波后的图像')