2020北航计算机夏令营机试题目讲解

一、二叉树(60分)
给你一个整数序列，用这些数构成一个完全二叉排序树，输出此二叉树的层序遍历序列。
输入的第一行是一个整数n，表示这个整数序列的长度，输入的第二行包含n个整数，每个数代表完全二叉排序树的一个节点，现在需要输出由这n个整数构成的完全二叉排序树的层序遍历序列。

输入样例：

18
56 987 -25 0 1021 -238 399 12 77 -1 72190 -25 -168 -41367 3218 12 0 -25

输出样例：

12 -1 987 -25 0 77 3218 -238 -25 0 12 56 399 1021 72190 -41367 -168 -25

样例解释：
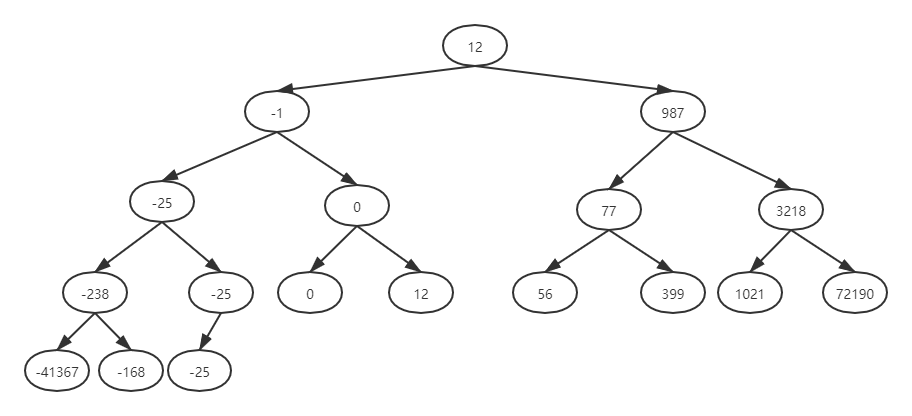
输入样例对应的完全二叉排序树如下图所示
在这里插入图片描述
思路分析
二叉排序树有一个特点，它的中根序列是非递减的，因此如果对输入的序列进行非递减排序，那么就相当于得到了这棵树的中根遍历序列，然后再根据这棵树是完全二叉树，就可以得到此树的具体结构。当然，对于此题来说，我们完全没有必要真的将树的结构重构出来，我们只要能够想办法得到它的层序遍历序列即可。
假设现在有一棵节点数目为 $n$ 的完全二叉排序树，它的中序遍历序列的第一个元素在数组中的下标是 $l I d x$ ，那么我们可以做如下数学演算。

树的高度 $h=\lfloor log_2n \rfloor$ ，高度从0开始。
除去最后一层，树的其余节点的数目 $remain=2^h-1$ 。
树的最后一层的节点数目 $l a s t = n - r e m a i n$ 。
理论上，高度为h的完全二叉树的最后一层可以有的节点数目 $lastMax=2^ h$ 。
记左子树的节点数目为 $l N u m$ 。
若 $\ge lastNum/2$ ，则说明左子树是满二叉树， $lNum=2^h-1$ 。
若 $l a s t < l a s t N u m / 2$ ，则说明左子树的最后一层没有填满， $lNum=2^{h-1}-1+last$
根节点在数组中的下标 $r o o t I d x = l I d x + l N u m$ 。
左子树中序遍历序列的第一个元素在数组的下标是 $l I d x$ ，长度为 $l N u m$ 。
右子树中序遍历序列的第一个元素在数组的下标是 $r o o t I d x + 1$ ，长度是 $n - l N u m - 1$ 。

通过上述的数学演算，可以根据中序遍历序列求出这棵完全二叉排序树的根节点，因为现在要求的是层序遍历序列，所以不能用递归的方法求左子树和右子树的根节点，而应该用队列来求。

源代码

#include <bits/stdc++.h>
using namespace std;
int arr[105];
queue < pair<int, int> > q;//求在arr数组中，从lIdx开始，长度为n的序列所构成的完全二叉排序树的根节点
void root(int lIdx, int n) {if (n <= 0)return;int h;          //树的高度，从0开始int lNum;       //左子树节点数目int remain;     //除去最后一层，其余节点的数目int last;       //最后一层的节点数目int lastMax;    //理论上，最后一层可以有的最大节点数目int rootIdx;    //根节点在数组中的下标h = log2(n);//在由float转为int的过程中，会自动实现向下取整remain = pow(2, h) - 1;last = n - remain;lastMax = pow(2, h);if (last >= lastMax / 2)lNum = pow(2, h) - 1;elselNum = pow(2, h - 1) - 1 + last;rootIdx = lIdx + lNum;cout << arr[rootIdx] << " ";q.push(make_pair(lIdx, lNum));q.push(make_pair(rootIdx + 1, n - lNum - 1));
}
int main()
{int n;cin >> n;for (int i = 1; i <= n; i++) cin >> arr[i];sort(arr + 1, arr + n + 1);q.push(make_pair(1, n));while (!q.empty()) {auto top = q.front();q.pop();root(top.first, top.second);}return 0;
}
/*
18
56 987 -25 0 1021 -238 399 12 77 -1 72190 -25 -168 -41367 3218 12 0 -2512 -1 987 -25 0 77 3218 -238 -25 0 12 56 399 1021 72190 -41367 -168 -25
*/

二、栈(40分）
给你一个函数调用过程，求调用的最大嵌套深度所对应的函数名，并输出调用路径，同时输出这个函数父函数（调用者）的个数和被调用的次数。同一个函数，如果有多条调用路径都可使其嵌套深度最深，则只输出第一条调用路径。
输入的数据中，若为1 funcName的形式，则表示调用funcName这个函数，若输入的是0，则表示结束对嵌套深度最大的函数的调用。
先看第一个测试用例。

1 main
1 input
0
1 area
0
1 findA
1 area
0
0
1 findB
1 get
0
0
0

首先是对main函数的调用，调用之前栈中什么也没有，调用之后栈中只有main函数，如下图所示。
在这里插入图片描述
main函数调用input函数
input函数调用结束

main函数调用area函数

area函数调用结束

main函数调用findA函数

findA函数调用area函数

area函数调用结束
在这里插入图片描述
findA函数调用结束

main函数调用findB函数

findB函数调用get函数
在这里插入图片描述

get函数调用结束
在这里插入图片描述

findB函数调用结束
在这里插入图片描述

main函数调用结束
在这里插入图片描述
从上面的调用过程可以看出，最大嵌套深度是3，对应的函数有两个，分别是area和get。area的调用路径是main-findA，总共有两个函数调用过area，这两个函数分别是input和findA，area总共被调用过两次。get的调用路径是main-findB，总共有一个函数调用过get，这个函数是findB。所以上面的测试用例输出结果应该是：

area main-findA 2 2
get main-findB 1 1

下面再来看一个更复杂一点的测试用例。

1 main
1 input
0
1 mysqrt
0
1 findA
0
1 findB
1 area
1 mysin
0
1 mycos
0
1 mysqrt
0
0
0
1 findC
1 area
1 mysin
0
0
1 mysqrt
1 max
0
0
0
1 output
0
0

对于这组输入数据，仍然可以用前面画栈结构图的方法来表示调用过程，限于篇幅，我这里就不再画了。大家应该注意到，对于这组数据，函数的调用次数和调用者的个数已经不再相同，这是因为一个函数可能多次调用另一个函数，比如area函数调用了两次mysin函数，那么mysin函数的调用者的个数是1，因为只有area函数对其进行过调用，但是调用次数却是2，因为它被调用了两次。同时还要注意，mysin函数有两条最深调用路径，分别是main-findB-area-mysin和main-findC-area-mysin，按照之前说过的输出规则，对于同一个函数，如果有多条最深调用路径，只输出第一条，所以最终的输出结果如下。

mysin main-findB-area 1 2
mycos main-findB-area 1 1
mysqrt main-findB-area 3 3
max main-findC-mysqrt 1 1

思路分析
这道题虽然看起来像是考察栈，但是却不能直接用C++STL中的stack，因为需要记录栈中的内容，用stack操作起来会非常麻烦，所以最终我选择用vector<string>来模拟栈，变量depth相当于栈顶指针，当发生函数调用时，先将被调函数入栈，再令depth自加，当调用结束时，直接令depth自减。
因为本题是一道模拟题，不涉及复杂的算法，所以不再进行过多的阐述，我已经在代码中加了详细的注释，读者可以边阅读代码，边体会解题过程。

源代码

#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
vector<string> callStack;	//相当于栈，存放函数名
unordered_map<string, int> numOfCalls;	//调用次数
unordered_map<string, unordered_set<string> > numOfCaller;	//统计有多少个父函数，用unordered_set的目的是去重
vector<vector<string> > ans;	//存放最终结果int main() {callStack.resize(205);int type;string funcName;int depth = 0, maxdep = 0;	//分别是当前的调用深度和目前为止最大的调用深度while (cin >> type) {if (type == 1) {//函数调用cin >> funcName;numOfCalls[funcName]++;	//记录函数被调用的次数if (depth != 0) {//深度不为0，说明当前被调用的函数一定有调用者（如果当前被调用的函数是main，则无调用者）string caller = callStack[depth - 1];numOfCaller[funcName].insert(caller);//将funcName函数的所有调用者都保存起来}callStack[depth++] = funcName;//先将funcName入栈，再令调用深度加1if (depth > maxdep) {//更新最大深度ans.clear();ans.push_back(callStack);maxdep = depth;}else if (depth == maxdep) {//最大深度相同int flag = false;	//判断是否有同一个函数，存在多条最深路径的情况for (auto v : ans) {if (v[maxdep - 1] == funcName) {flag = true;break;}}if(flag == false)ans.push_back(callStack);}}else {//调用结束depth--;}}for (int j = 0; j < ans.size(); j++) {funcName = ans[j][maxdep - 1];	//嵌套深度最大的函数cout << funcName << " " << ans[j][0];for (int i = 1; i < maxdep - 1; i++)	//输出调用路径cout << "-" << ans[j][i];cout << " " << numOfCaller[funcName].size() << " " << numOfCalls[funcName] << endl;}return 0;
}