二叉树作为一种常见的数据结构,我们在学习的过程中会经常用到.
当我们做课设的时候,能把二叉树图形化的打印出来无疑是一个加分项,所以今天我们就来探讨一下如何图形化的打印出二叉树来.
目录
分析阶段
如何打印
如何将数据存入打印数组
代码实现
存储结构定义
二叉树的创建
求深度
打印功能的代码实现
测试运行
分析阶段
如何打印
我们要完成二叉树的打印,至少要保证所有的节点都能打印在屏幕上而不冲突,而一个二叉树节点最多的情况就是满二叉树.所以我们只需要想好满二叉树如何打印出来便可.
打印二叉树需要以二叉树的遍历为基础,我们要打印出每一个节点就需要对每一个节点进行遍历,在遍历二叉树时递归的先序(中序,后序)更为简单.而控制台打印时只能一行一行的打印,所以我们可以将要打印出来的图形先存储到一个数组中.
存在数组就必定要有大小,数组的大小取决于我们二叉树的高度.
只有一个根节点的二叉树只需要一个1×1的数组就可以存储开
| 1 |
当有一个根节点及其左右孩子时,我们便需要5×3的数组来存储(为了美观起见,加上了斜杠和反斜杠)
| 1 | ||||
| / | \ | |||
| 1 | 1 |
让我们在加一层,当二叉树达到三层时,需要13×7的数组来存放
| 1 | ||||||||||||
| / | \ | |||||||||||
| / | \ | |||||||||||
| / | \ | |||||||||||
| 1 | 1 | |||||||||||
| / | \ | / | \ | |||||||||
| 1 | 1 | 1 | 1 |
通过总结规律我们发现,要能打印出完整的二叉树,宽度要依据最后一行的叶子节点的个数而来.而为了让它显的匀称我们让每个叶子节点之间相隔三个宽度,经计算存储一颗二叉树需要的数组宽度是
宽度=(2^(n-1)-1)*3+2^(n-1) n为层数化简可得
宽度=2^(n+1)-3 n为层数接下来计算高度,二叉树的每一层节点只需要一个高度,但层与层之间的连线高度确是不一样的.从上往下看时,当总层数只有两层时,第一层与第二层之间连线占一格高,当层数为三层时,第一层与第二层之间的连线占三格高.所以从上往下看,很难找到连线所占高度的规律.
这时不妨从下往上找,可以发现,倒数第一层与倒数第二层之间的连线高度必为1,倒数第二层与倒数第三层之间的高度必为3.倒数第三层与倒数第四层之间的连线高度必为7.到这里我们可以总结出一条规律,层与层之间的连线,必是2的n次方减一.
最后我们得出,对这个数组需要申请的内存大小是
宽度=2^(n+1)-3
高度=2^n-1
n为层数如何将数据存入打印数组
在生成打印数组时我们可以先将根节点放入整个数组第0行的最中间位置,然后查看有无左右孩子,若有则将左右孩子当成新的根节点进行递归.
代码实现
存储结构定义
我们用二叉链表来作为二叉树的存储结构
typedef struct TreeNode{char data; //数据域struct TreeNode * lchild,* rchild; //左右孩子指针
}TreeNode,*P_Node;二叉树的创建
我们将通过从控制台读取字符串的形式来创建二叉树
规则如下:
将二叉树写成先序遍历串,以 根-左孩子-右孩子 的形式组成
每个节点为单个字符
若该节点处无孩子则写成'.'

上图的二叉树就可以写成:ABC..DE.G..F...
//创建树,将输入的字符串以先序的形式存入二叉树
void CreateTree(P_Node &T)
{char ch;scanf("%c",&ch);if(ch == '\n'){return;}if(ch == '.'){T = NULL;return;}T = (P_Node)malloc(sizeof(TreeNode));T->data = ch;CreateTree(T->lchild);CreateTree(T->rchild);
}求深度
在生成打印数组时我们就需要用到二叉树的深度,也就是层数,所以我们也需要实现求深度的功能(递归实现)
//求深度
int DeepTree(P_Node T)
{if(!T){return 0;}return DeepTree(T->lchild)>DeepTree(T->rchild)?DeepTree(T->lchild)+1:DeepTree(T->rchild)+1;
//关键代码:如果该节点的左子树深度大于右子树则将左子树的深度加一返回,这个返回值便是以该节点做根节点的树的深度,右子树深度大时则相反
}打印功能的代码实现
做好了前置工作,本文的重点来了.
首先设置全局变量width和height,这两个值在两个函数中都会用到,所以设置成全局的.
int width,height;同时我们规定,数组类型为char,用一串连续的空间代替二维数组,数组中存的值与打印出来的效果对应如下表.
| -1 | 打印'/' |
| 1 | 打印'\' |
| 0 | 打印空格 |
| 其他 | 直接打印字符 |
要实现打印功能我们需要将需要用到递归的部分独立出来作为一个递归函数.此函数功能为先序遍历二叉树,同时向打印数组填入内容.
//T为二叉树的根节点,a是数组的起始地址,i,j是当前节点在数组中的位置
//如果节点有孩子,其孩子的j坐标为 j±(height-i+1)/2
void fillArray(P_Node &T,char *a,int i, int j)
{int ti,tj;if(T) //如果该位置有节点{*(a+(i*width)+j) = T->data; //向数组该点填入字符if(T->lchild) //有左右孩子给对应的连接线,左右孩子的值在下一层递归赋{//将该点与其左孩子之间的连线全部填上'/'for(ti=i+1,tj=j-1;tj>j-(height-i+1)/2;tj--){*(a+((ti)*width)+tj) = -1;ti++;}}if(T->rchild){for(ti=i+1,tj=j+1;tj<j+(height-i+1)/2;tj++){*(a+((ti)*width)+tj) = 1;ti++;}}//经过循环,ti恰好指到其孩子所在的层fillArray(T->lchild, a, ti, j-(height-i+1)/2);fillArray(T->rchild, a, ti, j+(height-i+1)/2);}
}计算宽高及实现打印功能的函数
void printBiTree(P_Node &T)
{int i,j;int n = DeepTree(T); //计算出深度n//在计算机中数据以二进制形式存储,所以一个数据左移1位就相当于乘以2的1次方width = (2<<n)-3; // 2^(n+1)-3height = (2<<(n-1))-1; // 2^n-1char *a = (char *)malloc(sizeof(char) * (width*height)); // 申请空间// 空间初始化为0for(i=0;i<height;i++){for(j=0;j<width;j++){*(a+(i*width)+j) = 0;}}//调用之前定义好的函数,填充打印数组fillArray(T, a, 0, (width-1)/2);//根据打印数组的内容来实现打印for(i=0;i<height;i++){for(j=0;j<width;j++){if(*(a+(i*width)+j) == -1){printf("/");}else if(*(a+(i*width)+j) == 1){printf("\\");}else if(*(a+(i*width)+j) == 0){printf(" ");}else{printf("%c", *(a+(i*width)+j));}}printf("\n");}
}测试运行
用例1: AB..B..

用例2: ABC..C..BC..C..

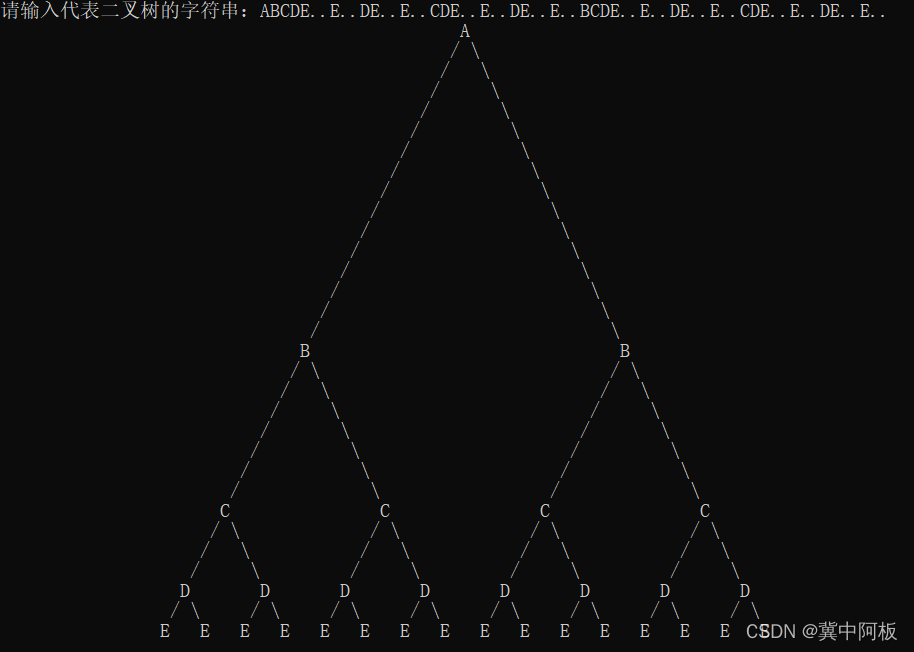
用例3: ABCD..D..CD..D..BCD..D..CD..D..

用例4: