一、基本原理
测量平差是德国数学家高斯于1821~1823年在汉诺威弧度测量的三角网平差中首次应用,以后经过许多科学家的不断完善,得到发展,测量平差已成为测绘学中很重要的、内容丰富的基础理论与数据处理技术之一。
图一 三角网平差
由于测量仪器的精度不完善和人为因素及外界条件的影响,测量误差总是不可避免的。为了提高成果的质量,处理好这些测量中存在的误差问题,观测值的个数往往要多于确定未知量所必须观测的个数,也就是要进行多余观测。有了多余观测,势必在观测结果之间产生矛盾,测量平差的目的就在于消除这些矛盾而求得观测量的最可靠结果并评定测量成果的精度。测量平差采用的原理就是“最小二乘法”。
测量平差是用最小二乘法原理处理各种观测结果的理论和计算方法。测量平差的目的在于消除各观测值间的矛盾,以求得最可靠的结果和评定测量结果的精度。任何测量,只要有多余观测,就有平差的问题。
二、项目中的平差
随着测绘成果不断的电子化与信息化,测量平差的概念很少被人体及,生产工具的不断进步和项目生产管理体系的科学化使得多数地信类项目不在需要进行平差。
实际上在我们做项目的过程中还是有很多项目需要进行平差计算的,如国土调查类项目,这部分数据最终都是要回归椭球面积进行面积控制,所以必须要进行平差。

图二 三调相关规范中面积控制部分目录
而在实际项目生产中的平差是怎样的呢?
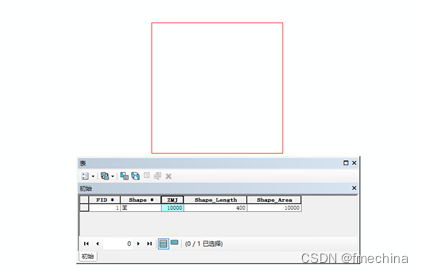
图三 为面积为10000平方米的矩形图斑
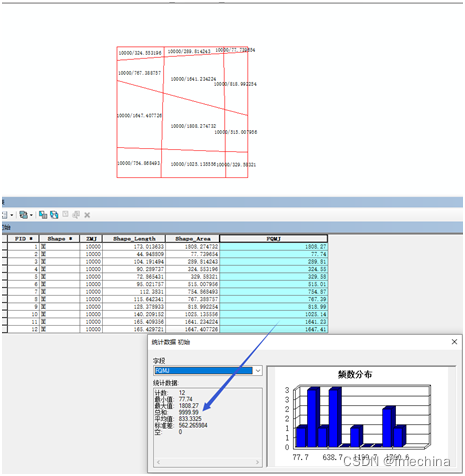
图四 矩形分割后并且面积保留两位小数后的汇总面积
从这里我们可以看到经过图斑分割在按精度计算面积后,发现计算后的面积总和与原图斑面积存在“0.01”的误差。而实际项目生产或者数据统计过程中这样的误差我们是经常遇见的,所以平差的概念通俗的讲就是将生产过程中的误差平均处理掉。即上面图示的“0.01”的误差处理掉。
这是我们项目生产过程中需要进行平差的第一个原因:数据运算过程中的表达误差。理论上面积为10000的图斑分成N个小图斑后,Sn=10000,但是我们面临更多的是单个小图斑的面积数值在一定范围无法取整,面积统计过程中进行了“四舍五入”后会面临数据值精度的损失,
这里延伸出来的就是我们的测量数据的值如何回归法定数值,如土地利用现状调查项目(三调)最后需要回归到地球的椭球面积。
椭球面积计算公式及要求
(一)椭球面上任一梯形图块面积


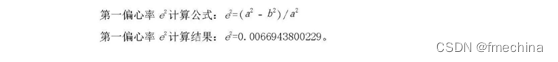
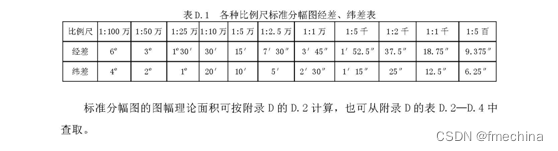
(二)图幅理论面积


(三)高斯投影反解变换公式
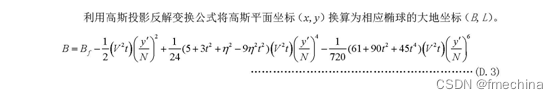

(四)任意图斑椭球面积计算




(五)计算用到的常数、椭球参数

(六)计算中的取位及要求

通过三调面积计算的相关规范不难看出椭球面积的计算过程中不同的算法模型已经精度取值方式会造成椭球面积的误差,但是一般情况下在默认的的容差范围内都是允许的。
当重新计算的椭球面积出现不一致且误差在允许误差之内时也就说明最后的汇总面积是会有误差的。
回归到问题本身,某项目测区为整个行政区域范围A,测量(调查)后在测区内形成了990个成果图斑,理论上成果图斑的总面积S(sum)=行政区域范围总面积S,目前已知行政区域总面积S为椭球面积,且计算方法是根据上一级行政区划结合测量平差而来,我们要想得到测量成果的汇总椭球面积的成果为S,那我们就必须不得不以S为控制面积,对每一个内部图斑先计算椭球面积,在整体考虑如何较为科学的得到S这个数值。这个过程就是我们项目中的平差工艺流程产生的根源。
三、手动平差的相关经验
在遇到平差问题的时候我毫不犹豫的认为FME是可以实现的,但是对于平差的过程以及具体方法不是十分了解,便在相关社群对有经验的老司机进行了请教学习。最后归纳整理得出以下几种方案:
(一)三调项目中,有相对应的软件进行平差计算。
有三调软件的都是直接将图斑调入软件进行平差计算,最后输出结果。这里我们只了解技术方案,所以可以得出结论就是这是一个可以自动化完成的工作。
(二)在二调项目中,没有相关的软件供人们使用,多半是手工进行平差计算。
经历过二调的测绘人现在都应该是行业老司机了,没有只能软件的年代全凭人工计算,不得不说佩服。但是据深入了解在数据处理过程中老前辈们还是结合Excel办公软件做了一套自动平差数值的模板,只需要将图斑的唯一值和面积值保留,导出Excel文件,将内容复制到模板Excel中,内置的相关算法就可以快速的将平差后的面积计算出来,最后再挂接关联到矢量数据中就完成了平差。
Excel表格平差的模板文件
(三)现今手头没有平差计算软件的采用了ArcGIS软件进行平差计算。
前面两种方案我并没有仔细去了解椭球面积是如何计算的,但是椭球面积的计算如果使用手工,不免是一个巨大的工作量。进一步请假其他前辈得知现阶段用的最广泛的就是使用ArcGIS软件人工按照既定的流程进行操作。最后也能得出平差值,但是会出现个别图斑最后的平差面积与相关质检软件计算的平差值不一致的情况,需要后面进行整改。
四、利用FME软件进行平差流程的搭建
(一)确定控制面积
控制面积的来源一般有两种方式,第一种是直接使用的控制面积,第二种就是需要间接进行计算平差的控制面积。
这里说到间接使用控制面积进行平差来求取控制面积似乎有一些使问题陷入循环的转态,但是事实上这样做是相对科学的方法论。
如:测区范围为1平方公里(控制面积)我在着一平方公里的范围内的图斑直接使用这个1平方公里的面积来控制平差是没有问题的,但是当我们面临的测区范围有5000平方公里的时候我们直接使用就不是很科学了。
在早期的测试中,直接利用5000平方公里做控制面积计算后得出的值可能误差就比较大。
所以才采用了多级控制的办法,将5000平方公里按照方格网法进行划分(如果有多级行政区划的时候建议用多级行政区划进行间接控制)为9个分区,对这9个区域进行平差计算,再将每个区域内的图斑参照单个区域的面积进行控制平差。
只要利用FeatureMerger进行关联传递。
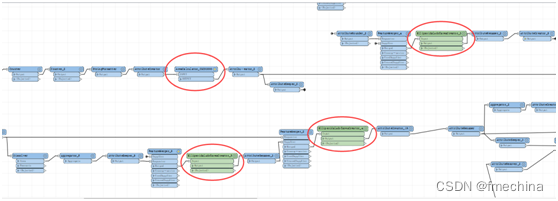
多级控制平差
(二)计算椭球面积
椭球面积的计算在FME中使用AreaCalculator_CGCS2000转换器直接进行椭球面积计算。
(三)平差方案的优化
平差简单来说就是用“多减少补”的科学的将误差消弭在每一个图斑中,是的整体面积一控制面积一致。
严格来说多级平差就是平差方案优化的一种形式,主要是避免出现异常值。
再就是平差方式的选择(即如何将误差值合理分配给每一个参与评查的要素)。很明显,加权的平均方式是最为合理的,根据图斑面积的参与度来进行进行权重配比分配。
但是即使使用加权的方式进行平差后也不是立马就达到平差效果了,还需要再次计算比较汇总面积与控制面积的数值是否一致。多数情况是不一致的,是由于权重平差采用了比例的方式,比例计算中涉及小数点位数的取舍,所以会出现小数点后几位的不一致。
这里采用大图斑均摊的原则(实际上这里产生的差值按照最小精度单位份数统计是小于图斑总数的)进行再次“摊派”,直到达到控制面积。
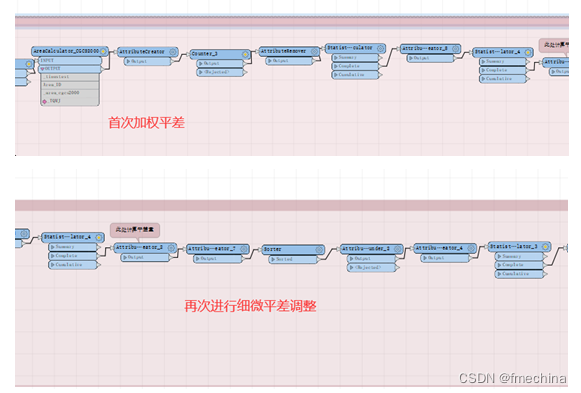
这里主要分享的对矢量数据的椭球面积进行计算再平差,平差其实在其他方面也是可以用到的,比如三调项目的流量统计(报表)中也会因为数值精度取值不同产生统计值与目标总值的差异,这里也是需要用到平差的。也是可以利用FME进行流程搭建,快速处理。