简介

louvain算法由比利时鲁汶大学的 Vincent D.Blondel 等人于 2008 年提出，因其能以较高的效率计算出令人满意的社区识别结果，是近年来最多被提及和使用的社区识别算法。

Louvain算法是一种基于模块度(模块度越大则表明社区划分效果越好。Q值的范围在[-0.5,1），论文表示当Q值在0.3~0.7之间时，说明聚类的效果很好。)的社区发现算法。其基本思想是网络中节点尝试遍历所有邻居的社区标签，并选择最大化模块度增量的社区标签。在最大化模块度之后，每个社区看成一个新的节点，重复直到模块度不再增大。

相关准备

安装louvain

louvain目前版本是0.16

pip install python-louvain

安装`networkx`

Networkx是一个Python的包,可以用来创建和处理复杂的图网络结构。

pip install networkx

试运行

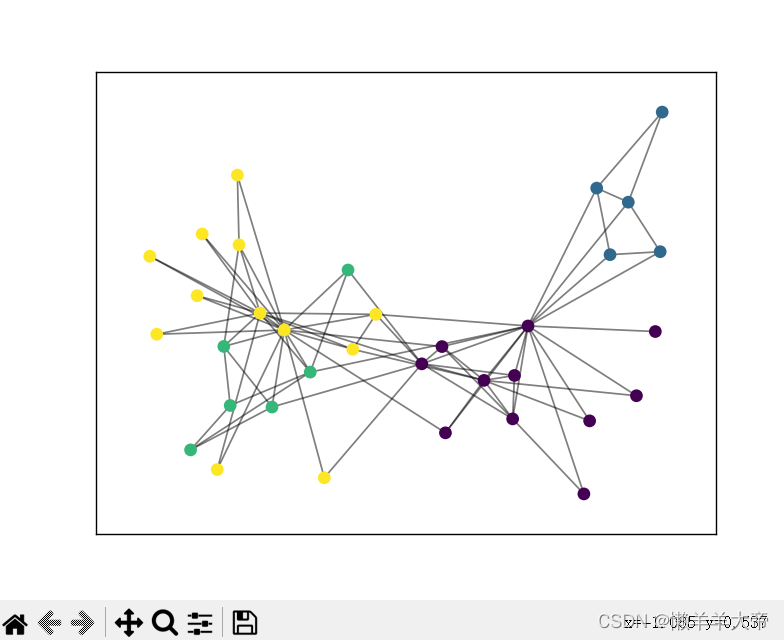
我在网上找了一个代码案例，看看是否能够正常的运行，不知道下面的代码是啥意思不要紧，只是测试安装的包是否能用。

import community as community_louvain
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import networkx as nx# load the karate club graph
G = nx.karate_club_graph()#first compute the best partition
partition = community_louvain.best_partition(G)# compute the best partition
partition = community_louvain.best_partition(G)# draw the graph
pos = nx.spring_layout(G)
# color the nodes according to their partition
cmap = cm.get_cmap('viridis', max(partition.values()) + 1)
nx.draw_networkx_nodes(G, pos, partition.keys(), node_size=40,cmap=cmap, node_color=list(partition.values()))
nx.draw_networkx_edges(G, pos, alpha=0.5)
plt.show()

算法描述

1. 模块度优化阶段

每个节点将自己作为自己社区标签。每个节点遍历自己的所有邻居节点，尝试将自己的社区标签更新成邻居节点的社区标签，选择模块度增量最大(贪婪思想)的社区标签，直到所有节点都不能通过改变社区标签来增加模块度。

也就是说，首先将每个节点指定到唯一的一个社区，然后按顺序将节点在这些社区间进行移动。怎么移动呢？假设有一节点 i ，它有三个邻居节点 j1, j2, j3，我们分别尝试将节点 i 移动到 j1, j2, j3 所在的社区，并计算相应的 modularity 变化值ΔQ，哪个变化值最大就将节点 i 移动到相应的社区中去（当然，这里我们要求最大的 modularity 变化值要为正，如果变化值均为负，则节点 i 保持不动）。按照这个方法反复迭代，直到网络中任何节点的移动都不能再改善总的 modularity 值为止。

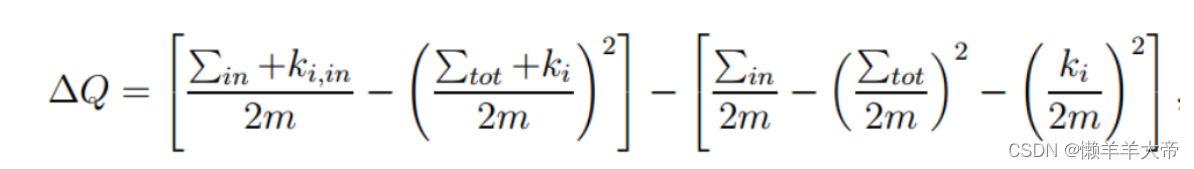
化简后：

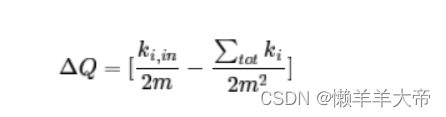
2. 网络凝聚阶段

每个社区合并为一个新的超级节点，超级节点的边权重为原始社区内所有节点的边权重之和，形成一个新的网络。

算法流程

1、初始时将每个顶点当作一个社区，社区个数与顶点个数相同。
2、依次将每个顶点与之相邻顶点合并在一起，计算它们最大的模块度增益是否大于0，如果大于 0，就将该结点放入模块度增量最大的相邻结点所在社区。
3、迭代第二步，直至算法稳定，即所有顶点所属社区不再变化。
4、将各个社区所有节点压缩成为一个结点，社区内点的权重转化为新结点环的权重，社区间权重转化为新结点边的权重。
5、重复步骤1-3，直至算法稳定。