K-means方法是一种非监督学习的算法,它解决的是聚类问题。
1、算法简介:K-means方法是聚类中的经典算法,数据挖掘十大经典算法之一;算法接受参数k,然后将事先输入的n个数据对象划分为k个聚类以便使得所获得的聚类满足聚类中的对象相似度较高,而不同聚类中的对象相似度较小。
2、算法思想:以空间中k个点为中心进行聚类,对最靠近他们的对象归类,通过迭代的方法,逐次更新各聚类中心的值,直到得到最好的聚类结果。
3、算法描述:
(1)适当选择c个类的初始中心;
(2)在第k次迭代中,对任意一个样本,求其到c各中心的距离,将该样本归到距离最短的那个中心所在的类;
(3)利用均值等方法更新该类的中心值;
(4)对于所有的C个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束;否则继续迭代。
4、算法举例:
我们假设药物A、B、C、D有两个特征值,分别是药物重量以及PH值。
| 药物名称 | 药物重量 | 药物PH值 |
|---|---|---|
| A | 1 | 1 |
| B | 2 | 1 |
| C | 4 | 3 |
| D | 5 | 4 |
现在我们要对这四个药物进行聚类,已知我们要分成两类,那么我们该怎么做呢?
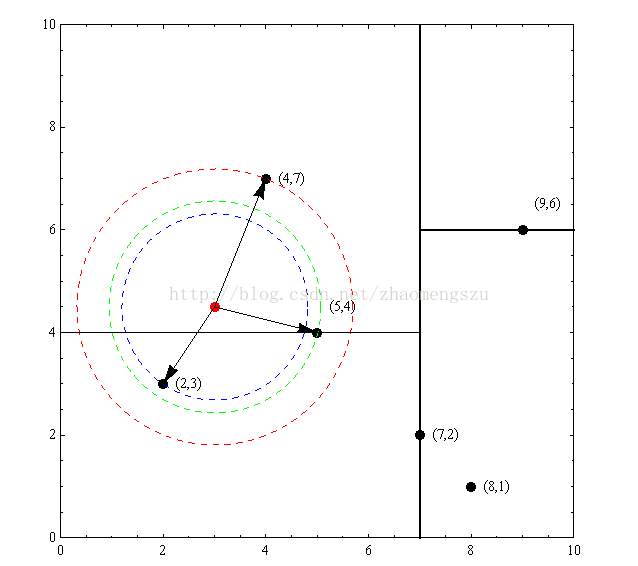
首先我们把上面的数据画到二位坐标系当中 A(1,1),B(2,1),C(4,3),D(5,4) :

初始时,我们先假设药物A为聚类1的中心点,B为聚类2的中心点,那么初始时的中心坐标分别为 c1=(1,1),c2=(2,1) ,矩阵D的第一行代表各个点到中心点 c1 的距离,第二行代表各个点到中心点 c2 的距离;那么初始矩阵 D0 表示成如下:
矩阵 G 代表样本应该归属于哪个聚类,第一行代表各个点是否属于中心
由矩阵 G0 可知A药物属于一个类,B、C、D属于一类;
然后,利用均值等方法更新该类的中心值。

上图是更新后的坐标图,对应的中心点也发生了变化。
因为中心点跟上次不一样了,所以我们又可以对样本点进行重新划分。划分的方法还是跟以前一模一样,我们先计算出矩阵 D1 表示成如下:
此时 G1 表示成如下:
由矩阵 G1 可知A、B药物属于一个类,C、D属于一类;
然后,利用均值等方法再次更新该类的中心值。

上图是更新后的坐标图,对应的中心点也发生了变化。
因为中心点跟上次不一样了,所以我们又可以对样本点进行重新划分。划分的方法还是跟以前一模一样,我们先计算出矩阵 D2 表示成如下:
此时 G2 表示成如下:
由矩阵 G2 可知A、B药物属于一个类,C、D属于一类;
然后,利用均值等方法再次更新该类的中心值。
因为对应的中心点并没有发生变化,所以迭代停止,计算完毕。
本算法的时间复杂度:O(tkmn),其中,t为迭代次数,k为簇的数目,m为记录数,n为维数;
空间复杂度:O((m+k)n),其中,k为簇的数目,m为记录数,n为维数。
适用范围:
K-menas算法试图找到使平凡误差准则函数最小的簇。当潜在的簇形状是凸面的,簇与簇之间区别较明显,且簇大小相近时,其聚类结果较理想。前面提到,该算法时间复杂度为O(tkmn),与样本数量线性相关,所以,对于处理大数据集合,该算法非常高效,且伸缩性较好。但该算法除了要事先确定簇数K和对初始聚类中心敏感外,经常以局部最优结束,同时对“噪声”和孤立点敏感,并且该方法不适于发现非凸面形状的簇或大小差别很大的簇。
缺点:
1、聚类中心的个数K 需要事先给定,但在实际中这个 K 值的选定是非常难以估计的,很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适;
2、Kmeans需要人为地确定初始聚类中心,不同的初始聚类中心可能导致完全不同的聚类结果。(可以使用K-means++算法来解决)
算法代码实现:
main.m
clear all;
close all;
clc;%第一类数据
mu1=[0 0 0]; %均值
S1=[0.3 0 0;0 0.35 0;0 0 0.3]; %协方差
data1=mvnrnd(mu1,S1,100); %产生高斯分布数据%%第二类数据
mu2=[1.25 1.25 1.25];
S2=[0.3 0 0;0 0.35 0;0 0 0.3];
data2=mvnrnd(mu2,S2,100);%第三个类数据
mu3=[-1.25 1.25 -1.25];
S3=[0.3 0 0;0 0.35 0;0 0 0.3];
data3=mvnrnd(mu3,S3,100);%显示数据
plot3(data1(:,1),data1(:,2),data1(:,3),'+');
hold on;
plot3(data2(:,1),data2(:,2),data2(:,3),'r+');
plot3(data3(:,1),data3(:,2),data3(:,3),'g+');
grid on;%三类数据合成一个不带标号的数据类
data=[data1;data2;data3]; %这里的data是不带标号的%k-means聚类
[u re]=KMeans(data,3); %最后产生带标号的数据,标号在所有数据的最后,意思就是数据再加一维度
[m n]=size(re);%最后显示聚类后的数据
figure;
hold on;
for i=1:m if re(i,4)==1 plot3(re(i,1),re(i,2),re(i,3),'ro'); elseif re(i,4)==2plot3(re(i,1),re(i,2),re(i,3),'go'); else plot3(re(i,1),re(i,2),re(i,3),'bo'); end
end
grid on;
K-Means.m
%N是数据一共分多少类
%data是输入的不带分类标号的数据
%u是每一类的中心
%re是返回的带分类标号的数据
function [u re]=KMeans(data,N) [m n]=size(data); %m是数据个数,n是数据维数ma=zeros(n); %每一维最大的数mi=zeros(n); %每一维最小的数u=zeros(N,n); %随机初始化,最终迭代到每一类的中心位置for i=1:nma(i)=max(data(:,i)); %每一维最大的数mi(i)=min(data(:,i)); %每一维最小的数for j=1:Nu(j,i)=ma(i)+(mi(i)-ma(i))*rand(); %随机初始化,不过还是在每一维[min max]中初始化好些end endwhile 1pre_u=u; %上一次求得的中心位置for i=1:Ntmp{i}=[]; % 公式一中的x(i)-uj,为公式一实现做准备for j=1:mtmp{i}=[tmp{i};data(j,:)-u(i,:)];endendquan=zeros(m,N);for i=1:m %公式一的实现c=[];for j=1:Nc=[c norm(tmp{j}(i,:))];end[junk index]=min(c);quan(i,index)=norm(tmp{index}(i,:)); endfor i=1:N %公式二的实现for j=1:nu(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));end endif norm(pre_u-u)<0.1 %不断迭代直到位置不再变化break;endendre=[];for i=1:mtmp=[];for j=1:Ntmp=[tmp norm(data(i,:)-u(j,:))];end[junk index]=min(tmp);re=[re;data(i,:) index];endendK-means、和KNN算法比较
KNN(K-Nearest Neighbor)介绍
算法思路:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
看下面这幅图:
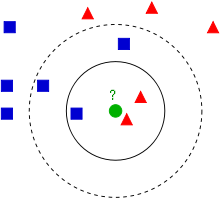
KNN的算法过程是是这样的:
从上图中我们可以看到,图中的数据集是良好的数据,即都打好了label,一类是蓝色的正方形,一类是红色的三角形,那个绿色的圆形是我们待分类的数据。
如果K=3,那么离绿色点最近的有2个红色三角形和1个蓝色的正方形,这3个点投票,于是绿色的这个待分类点属于红色的三角形
如果K=5,那么离绿色点最近的有2个红色三角形和3个蓝色的正方形,这5个点投票,于是绿色的这个待分类点属于蓝色的正方形
我们可以看到,KNN本质是基于一种数据统计的方法!其实很多机器学习算法也是基于数据统计的。
KNN是一种memory-based learning,也叫instance-based learning,属于lazy learning。即它没有明显的前期训练过程,而是程序开始运行时,把数据集加载到内存后,不需要进行训练,就可以开始分类了。
具体是每次来一个未知的样本点,就在附近找K个最近的点进行投票。
KNN和K-Means的区别

参考:
1、 Kmeans、Kmeans++和KNN算法比较
2、matlab练习程序(k-means聚类)
相关博客:
1、机器学习系列之机器学习之决策树(Decision Tree)及其Python代码实现
2、机器学习系列之机器学习之Validation(验证,模型选择)
3、机器学习系列之机器学习之Logistic回归(逻辑蒂斯回归)
4、机器学习系列之机器学习之拉格朗日乘数法
5、机器学习系列之机器学习之深入理解SVM