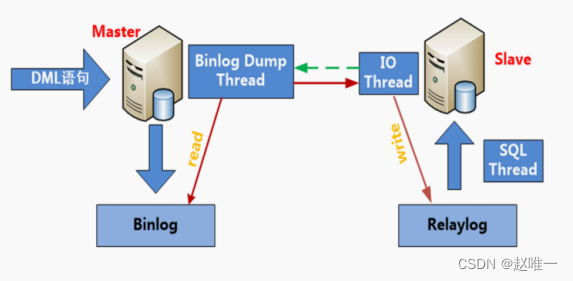
文章目录
- 方法一:穷举法
- 方法二:二分法
- 方法三:牛顿-拉夫逊算法
- 总结
方法一:穷举法
positive_num = int(input("输入一个正数:"))
#无穷逼近法
answer=0 #正数的根号结果
numGuess=0 #循环次数
epsilon=0.01 #精度
add_value=0.1 #每轮answer增长值
while abs(answer**2-positive_num) >=epsilon : #abs已经限制了anwer,在answer在小于5的时候就已经停了循环numGuess+=1 #记录循环次数answer+=add_value #answer的变化
print(numGuess,' ',answer)
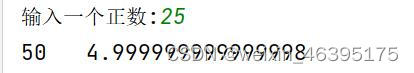
此方法通过从零开始每一轮加0.1的可以自行改变精度与增加值进行尝试,如果把增加值改为1,就可以得到根号25结果为5的答案。这种方法你也可以试着去掉epsilon这个参数试试,我觉得这个参数就是用来模仿高数中极限的思想的。也方便几个方法对比。
方法二:二分法
#二分法
positive_num = int(input("输入一个正数(origin_high):"))
low=0 #最小值
high = positive_num #最大值
answer=(low+high)/2 #定义answer
numGuess=0
epsilon=0.01
while abs(answer**2-positive_num) >=epsilon :numGuess+=1if answer**2<positive_num:low=answer #小了就把low调大else:high=answer #大了就把high调小answer=(low+high)/2 #夹击寻找答案
print(numGuess,' ',answer)

上下夹击寻找根号值,代码比穷举法多了一个if循环,但是循环次数明显减少,同样的epsilon,这里循环次数显著减少,所以说二分法比穷举法好啊,运算量小。
方法三:牛顿-拉夫逊算法
#牛顿-拉夫逊法
positive_num = int(input("输入一个正数:"))
epsilon=0.01
answer=positive_num/2 #答案肯定小于这个正数的一半
numGuess=0
while abs(answer**2-positive_num) >=epsilon:answer = answer - abs(answer**2-positive_num)/(2*answer) #answer每轮按照比率下降numGuess+=1
print(numGuess,' ',answer)

总结
一开始我也觉得各个方法里面的epsilon这个参数很多余,明明可以直接answer**2<=25就可以了,但对比去除了epsilon后的结果之后,我觉得还是加上更佳。三种方法的循环次数逐级递减,效率逐级升高。