并行程序设计——OMP编程

实验一

实验内容

分别实现课件中的梯形积分法的Pthread、OpenMP版本，熟悉并掌握OpenMP编程方法，探讨两种编程方式的异同。

实验代码

OpenMP编程

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>void Trap(double a, double b, int n, double *global_result_p);double f(double x) {return x * x;
}int main(int argc, char *argv[]) {double global_result = 0.0;double a, b;int n;int thread_count;thread_count = 5;printf("Enter a, b, and n\n");scanf("%lf %lf %d", &a, &b, &n);
# pragma omp parallel num_threads(thread_count)Trap(a, b, n, &global_result);printf("With n = %d trapezoids, our estimate\n", n);printf("of the integral from %f to %f = %.14e\n", a, b, global_result);return 0;
} /* main*/void Trap(double a, double b, int n, double *global_result_p) {double h, x, my_result;double local_a, local_b;int i, local_n;int my_rank = omp_get_thread_num();int thread_count = omp_get_num_threads();h = (b - a) / n;local_n = n / thread_count;local_a = a + my_rank * local_n * h;local_b = local_a + local_n * h;my_result = (f(local_a) + f(local_b)) / 2.0;for (i = 1; i <= local_n; i++) {x = local_a + i * h;my_result += f(x);}my_result = my_result * h;
# pragma omp critical*global_result_p += my_result;
} /* Trap*/

实验效果

请添加图片描述

pthread编程

#include <pthread.h>
#include <algorithm>
#include <stdio.h>
# include <stdlib.h>double f(double x) {return x * x;
}typedef struct {int threadId;
} threadParm_t;
const int THREAD_NUM = 5; //表示线程的个数
int next_task = 1;//从1开始
int seg = 50;//每次分50份
double totalSize = 0.000; //表示总面积
double h = 0.00;//表示间距
double a = 1.000, b = 8.000;
int n = 1000;
pthread_mutex_t barrier_mutex = PTHREAD_MUTEX_INITIALIZER;void cal(int i) {//计算第i分double x = a + i * h;double myResult = f(x) * h;pthread_mutex_lock(&barrier_mutex);totalSize += myResult;pthread_mutex_unlock(&barrier_mutex);
}void *SSE_pthread(void *parm) {int task = 0;while (true) {pthread_mutex_lock(&barrier_mutex);next_task += seg;task = next_task;pthread_mutex_unlock(&barrier_mutex);if (task - seg >= n) break;for (int i = task - seg; i < std::min(task, n); i++) {cal(i);}}pthread_exit(nullptr);
}int main(int arg, char *argv[]) {pthread_t thread[THREAD_NUM];threadParm_t threadParm[THREAD_NUM];for (int i = 0; i < THREAD_NUM; i++) {threadParm[i].threadId = i;}printf("Enter a, b, and n\n");scanf("%lf %lf %d", &a, &b, &n);//先计算两边的面积之和h = (b - a) / n;totalSize = h * (f(a) + f(b)) / 2;for (int i = 0; i < THREAD_NUM; i++) {pthread_create(&thread[i], nullptr, SSE_pthread, (void *) &threadParm[i]);}for (int k = 0; k < THREAD_NUM; k++) {pthread_join(thread[k], nullptr);}pthread_mutex_destroy(&barrier_mutex);printf("With n = %d trapezoids, our estimate\n", n);printf("of the integral from %f to %f = %.14e\n", a, b, totalSize);return 0;
}

实验结果

请添加图片描述
注：由于我的pthread求梯形的基准和OpenMP的基准不同，所以求的实验结果略有差异

两种编程方式的异同

OpenMP是根植于编译器的，更偏向于将原来串行化的程序，通过加入一些适当的编译器指令（compiler directive）变成并行执行，从而提高代码运行的速率。这样做是在没有OpenMP支持编译时，代码仍然可以编译。创建线程等后续工作需要编译器来完成。

而Pthread是一个库，所有的并行线程创建都需要我们自己完成。Pthread仅在有多个处理器可用时才对并行化有效，并且仅在代码针对可用处理器数进行了优化时才有效。因此，OpenMP的代码更易于扩展。

实验二

实验描述

对于课件中“多个数组排序”的任务不均衡案例进行OpenMP编程实现（规模可自己调整），并探索不同循环调度方案的优劣。提示：可从任务分块的大小、线程数的多少、静态动态多线程结合等方面进行尝试，探索规律。

实验代码

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <ctime>
#include <sys/time.h>
#include <algorithm>const int ARR_NUM = 1000; //固定数组大小
const int ARR_LEN = 4000; //固定数组长度
int THREAD_NUM = 4; //固定线程个数，改变粗颗粒分配大小
int seg = 10; //改变粗颗粒的分配大小
struct timeval startTime, stopTime;// timers
int arr[ARR_NUM][ARR_LEN];
int tempArr[ARR_NUM][ARR_LEN]; //用于暂时存储数组，控制变量唯一
int next_arr = 0;void OMP_sort();void init(int num) {srand(unsigned(time(nullptr)));for (int i = 0; i < num; i++) {for (int j = 0; j < ARR_LEN; j++)arr[i][j] = rand();}
}//使用冒泡排序，使变量唯一
void sort(int *a) {for (int i = 0; i < ARR_LEN - 1; ++i) {for (int j = i + 1; j < ARR_LEN; ++j) {if (a[j] < a[i]) {int temp = a[i];a[i] = a[j];a[j] = temp;}}}
}void store(int a[][ARR_LEN], int b[][ARR_LEN], int num) {for (int i = 0; i < num; i++) {for (int j = 0; j < ARR_LEN; j++)b[i][j] = a[i][j];}
}int main(int argc, char *argv[]) {init(ARR_NUM);store(arr, tempArr, ARR_NUM);for (; seg <= 100; seg += 10) {printf("seg: %d\n",seg);store(tempArr, arr, ARR_NUM);next_arr = 0;gettimeofday(&startTime, NULL);
# pragma omp parallel num_threads(THREAD_NUM)OMP_sort();gettimeofday(&stopTime, NULL);double trans_mul_time =(stopTime.tv_sec - startTime.tv_sec) * 1000 + (stopTime.tv_usec - startTime.tv_usec) * 0.001;printf("time :%lf ms\n", trans_mul_time);}return 0;
} /* main*/void OMP_sort() {int task = 0;while (true) {
#pragma omp critical //每次只能一个线程执行task = next_arr += seg;//每次动态分配seg个if (task - seg >= ARR_NUM) break;int min = task < ARR_NUM ? task : ARR_NUM;for (int i = task - seg; i < min; ++i) {sort(arr[i]);}}
} /* Trap*/

实验运行结果

请添加图片描述
如此进行多次重复实验，将得到的数据绘成echarts图表

实验图表和结论

请添加图片描述

实验结论

由以上图表可知，根据动态粗颗粒的分配的大小可知，各个分配结果的运行效率基本相似。
由上图可知，当每次分配数目为30的时候，运行时间最短，运行效率最快。但是当每次分配个数超过80时，运行效率也不低。由于此次实验总的数组的行数比较少，所以运行效率并不会相差很大，如若需要更加准确的数值的话，则需要加大数组的行数。

实验三（附加题）

实验内容

实现高斯消去法解线性方程组的OpenMP编程，与SSE/AVX编程结合，并探索优化任务分配方法。

实验代码

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
#include <ctime>
#include <sys/time.h>
#include <algorithm>
#include <pmmintrin.h>const int n = 2048;//固定矩阵规模，控制变量
const int maxN = n + 1; // 矩阵的最大值
float a[maxN][maxN];
float temp[maxN][maxN];//用于暂时存储a数组中的变量，控制变量唯一
const int THREAD_NUM = 4; //表示线程的个数
int seg = 30;//表示每次线程运行的行数，将来它会改变来探究最优任务分配方法
int next_task = 0;
int line = 0;//记录当前所依赖的行数
struct timeval startTime, stopTime;// timers/*** 根据第i行的元素，消除j行的元素* @param i 根据的行数* @param j 要消元的行数*/
void OMP_elimination(int i, int j) {float tep;__m128 div, t1, t2, sub;// 用temp暂存相差的倍数tep = a[j][i] / a[i][i];// div全部用于存储temp，方便后面计算div = _mm_set1_ps(tep);//每四个一组进行计算，思想和串行类似int k = n - 3;for (; k >= i + 1; k -= 4) {t1 = _mm_loadu_ps(a[i] + k);t2 = _mm_loadu_ps(a[j] + k);sub = _mm_sub_ps(t2, _mm_mul_ps(t1, div));_mm_store_ss(a[j] + k, sub);}//处理剩余部分for (k += 3; k >= i + 1; --k) {a[j][k] -= a[i][k] * tep;}a[j][i] = 0.00;
}/*** 多线程消元函数,动态粗颗粒分配，每次分配seg个* @param parm*/
void OMP_func() {int task = 0;while (true) {
#pragma omp critical //每次只能一个线程执行{task = next_task;next_task += seg;//每次分配seg个}if (task >= n) break;int min = task + seg < n ? task + seg : n;for (int i = task; i < min; ++i) {OMP_elimination(line, i);}}
}//用于矩阵改变数值,为防止数据溢出,随机数的区间为100以内的浮点数
void change() {srand((unsigned) time(NULL));for (int i = 0; i < n; i++) {for (int j = 0; j <= n; j++) {a[i][j] = (float) (rand() % 10000) / 100.00;}}
}/*** 将a数组的数据存储到b数组中* @param a* @param b*/
void store(float a[][maxN], float b[][maxN]) {for (int i = 0; i < n; i++) {for (int j = 0; j <= n; j++) {b[i][j] = a[i][j];}}
}int main(int arg, char *argv[]) {change();store(a, temp);// SSE算法消元设计for (; seg <= 300; seg += 30) {store(temp, a);//从temp中取数printf("seg: %d\n", seg);gettimeofday(&startTime, NULL);for (line = 0; line < n - 1; ++line) {next_task = line + 1;
# pragma omp parallel num_threads(THREAD_NUM)OMP_func();}gettimeofday(&stopTime, NULL);double trans_mul_time =(stopTime.tv_sec - startTime.tv_sec) * 1000 + (stopTime.tv_usec - startTime.tv_usec) * 0.001;printf("time: %lf ms\n", trans_mul_time);}
}

代码运行结果

请添加图片描述

如此重复多次实验，将所得到的的数据绘成echarts图表

实验图表和结论

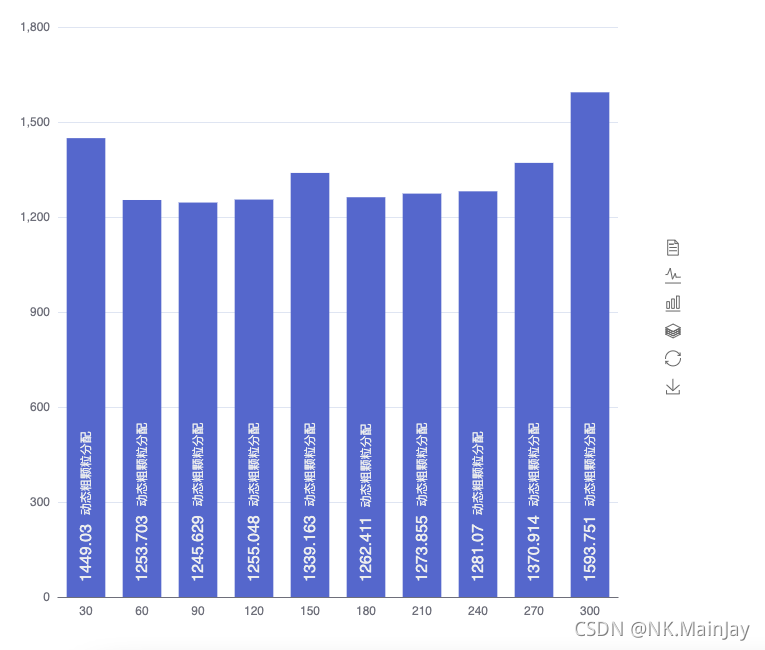
请添加图片描述
实验结论

与上个实验不同的是，这次实验我增加了整体矩阵的大小和每次分配行数的间距，这样得出的实验结果更加准确。
由上图表可知，当矩阵规模达到2048 $\times$ 2048时，整体运行的运行时间都相对较短，运行效率相比于串行化执行要快很多。每次分配90行的时候运行效果最佳，180~240的时候与90相差不大，整体区别不太。所以矩阵规模越大，尽量分配越多的行数使运行效率加快。