等价无穷小和泰勒公式

• 等价无穷小可以有泰勒公式推导(通用)
• 通过泰勒公式的变形,可以获得各式各样的等价无穷小
• 如果不使用泰勒公式,直接从极限的角度和函数的基本性质来证明,从中也可以学习到一些技巧,开阔思路

常用等价无穷小

• 后半部分相对不如第一部分常用(都可以通过泰勒公式推导)

泰勒公式&等价无穷小求解极限

• 带有peano余项的泰勒公式(maclaurin)公式,可以方便的求出一些函数的极限
• 例如

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{e^x-cosx-x}{ln(1+x^2)} \\ {e}^x=1+x+\frac{x^2}{2!}+o(x^2); \\ cosx=1-\frac{x^2}{2!}+o(x^2); \\ 于是,分子可以被统一为关于x的幂的形式(通过合并幂以及(有限个同阶等价无穷小)): \\ {e}^x-cosx-x=(1+x+\frac{x^2}{2!})-(1-\frac{x^2}{2})-x+o(x^2) \\ =x^2+o(x^2) \\ o(x^2)是x^2的高阶无穷小,有\underset{x\to 0}{\lim }\frac{o(x^2)}{x^2}=0 \\ 分母可以通过等价无穷小直接将(ln(1+x^2)替换为x^2) \\ 从而函数的(x\to 0)极限=\underset{x\to 0}{\lim }\frac{x^2+o(x^2)}{x^2} \\ =\underset{x\to 0}{\lim }(1+\frac{o(x^2)}{x^2})=1+0=1 \end{gathered}$$

无穷小量

• $如果\underset{x\to \ast }{\lim }f(x)=0,则称,f(x)为x\to \ast 时的无穷小量$

无穷小量的比较

• $下面用\lim 来简写\underset{x\to \ast }{\lim }$
  • $设\lim a(x)=0,\lim b(x)=0$
  • $记:k=k(a(x),b(x))=\lim \frac{a(x)}{b(x)}$
• 高阶无穷小:
  • $k=0$
    • 记为:$a(x)=o(b(x)),表示a(x)是b(x)同一个过程下的高阶无穷小$
• 低阶:
  • $k=\infty$
• 同阶:
  • $k=C\ne 0$
  • $等价:k=C=1$
    • 这是同阶的特殊情况!

无穷小的阶(相对阶)

$$\begin{gathered} 如果\lim \frac{a(x)}{(b(x){)}^k}=C\ne 0 \\ 则a(x)是b(x)的k阶无穷小 \end{gathered}$$

• 常用的等价无穷小比较多

  • 对于三角函数相关的等价无穷小,他们大多可以通过

    • 三角恒等式转换函数名
    • 配凑系数(依据第一重要极限):

    $$\underset{x\to 0}{\lim }\frac{sin(x)}{x}=1$$

  • 通常通过一下三角函数倍角公式:(将cos函数转化为sin进行利用第一重要极限)

    $$1-cosx=1-(1-2si{n}^2(x))=2si{n}^2\frac{x}{2}$$

    • $$\begin{gathered} 两边同乘以-1 \\ cosx-1=-2si{n}^2\frac{x}{2} \end{gathered}$$

利用等价无穷小来计算极限(代换原则)

• 总的来说,代换之后,不可以相互抵消(产生最高阶无穷小0 )

  • 

• 整个式子中的乘除因子可以用等价无穷小替换求极限

  • 加减的时候谨慎替换

  • 被求极限的表达式如果表示成$\sum e_i(x),并且e_i={\prod }_{}{t}_j(x)$

    • 那么对于$t_j$的替换属于局部替换,这是错误的替换

  • 例如:

    • $$\begin{gathered} \underset{x\to 0}{\lim }\frac{\ln (1+x)-x}{x^2}=\underset{x\to 0}{\lim }(\frac{\ln (1+x)}{x^2}-\frac{x}{x^2}) \\ 此处需要小心,不可以轻易将\ln (1+x)替换为x \\ \underset{x\to 0}{\lim }\frac{\ln (1+x)}{x^2}属于\frac{0}{0}型, \\ 可以考虑使用洛必达法则 \\ \underset{x\to 0}{\lim }(\frac{\ln (1+x)}{x^2}-\frac{x}{x^2})\ne \underset{x\to 0}{\lim }\frac{\ln (1+x)}{x^2}-\underset{x\to 0}{\lim }\frac{x}{x^2} \\ 因为,右侧中第二部分式无穷大,不满足基本极限的加减运算法则 \end{gathered}$$

等价无穷小充要条件

• $$\begin{gathered} x\to \ast 的过程中,a(x)-b(x)=o(b(x)) \\ a(x),b(x)调换顺序依然成立(a(x)\sim b(x)\iff b(x)\sim a(x)) \end{gathered}$$

  • $例如x^3+x^4\sim x^3,其中a(x)=x^3+x^4;b(x)=x^3$
    • $a(x)-b(x)=x^4=o(b(x))$
    • $b(x)-a(x)=-x^4=o(b(x))$

常用的等价无穷小和推导

$\sin (x)\sim x$

$$\underset{x\to 0}{\lim }\frac{sin(x)}{x}=1;第一重要极限$$

$tan(x)\sim x$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{tan(x)}{x}=1 \\ \underset{x\to 0}{\lim }\frac{sinx}{xcos(x)}=\underset{x\to 0}{\lim }\frac{sinx}{x}\frac{1}{cosx}=\underset{x\to 0}{\lim }(1\cdot \frac{1}{cosx})=\frac{\underset{x\to 0}{\lim }1}{\underset{x\to 0}{\lim }cos(x)}=1 \end{gathered}$$

$arcsin(x)\sim x$

$$\begin{gathered} 令t=arcsin(x),x=sin(t),t\to 0(x\to 0) \\ \underset{x\to 0}{\lim }\frac{arcsin(x)}{x}=\underset{t\to 0}{\lim }\frac{t}{sin(t)}=1 \end{gathered}$$

$arctan(x)\sim x$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{arctan(x)}{x}=1 \\ 令t=arctan(x), \\ x=tan(t); \\ \Rightarrow \underset{x\to 0}{\lim }\frac{arctan(x)}{x}=\underset{t\to 0}{\lim }\frac{t}{tan(t)}=1 \end{gathered}$$

$ln(1+x)\sim x$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{ln(1+x)}{x}=1 \\ 利用对数性质和第二重要极限证明 \\ \underset{x\to 0}{\lim }\frac{ln(1+x)}{x}=\underset{x\to 0}{\lim }\frac{1}{x}ln(1+x)=\underset{x\to 0}{\lim }ln(1+x{)}^{\frac{1}{x}}=\underset{x\to 0}{\lim }ln(e)=1 \end{gathered}$$

$lo{g}_a(1+x)\sim \frac{1}{ln(a)}x$

$$\begin{gathered} 更一般的,可有\underset{x\to 0}{\lim }\frac{lo{g}_a(1+x)}{\frac{1}{ln(a)}x}=1 \\ 根据换底公式(changebase) \\ {\log }_{a}e=\frac{ln(e)}{ln(a)}=\frac{1}{ln(a)} \\ \underset{x\to 0}{\lim }\frac{lo{g}_a(1+x)}{x}=\underset{x\to 0}{\lim }\frac{1}{x}lo{g}_a(1+x)=\underset{x\to 0}{\lim }lo{g}_a((1+x{)}^{\frac{1}{x}})=lo{g}_a(e)=\frac{1}{ln(a)} \\ \therefore lo{g}_a(1+x)\sim \frac{1}{ln(a)}x \end{gathered}$$

$e^x-1\sim x$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{e^x-1}{x}=1 \\ 换元法:令t=e^x-1; \\ t=(e^x-1)\to 0(x\to 0)即,有\underset{x\to 0}{\lim }x=\underset{t\to 0}{\lim }t=0 \\ 则x=ln(t+1) \\ \underset{x\to 0}{\lim }\frac{e^x-1}{x}=\underset{t\to 0}{\lim }\frac{t}{ln(t+1)}=1 \\ {e}^x-1\sim x \end{gathered}$$

$(a^x-1)\sim x\ln a$

更一般的,可有
$$\begin{gathered} (a^x-1)\sim x\ln a \\ original=\underset{x\to 0}{\lim }\frac{a^x-1}{x\ln a} \\ 令t=a^x-1; \\ t\to 0(x\to 0); \\ x=lo{g}_a(t+1) \\ lo{g}_a(1+t)\sim \frac{1}{ln(a)}t \\ original=\underset{t\to 0}{\lim }\frac{t}{{\log }_a(t+1)}=\underset{t\to 0}{\lim }\frac{t}{\frac{1}{\ln a}t}=\ln a \\ \therefore (a^x-1)\sim x\ln a \end{gathered}$$

$1-cos(x)\sim \frac{1}{2}{x}^2$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{1-cos(x)}{\frac{1}{2}{x}^2}=1 \\ 三角函数倍角公式cosx=co{s}^2(\frac{x}{2})-si{n}^2(\frac{x}{2}) \\ =1-2{\sin }^2(\frac{x}{2}),(cosx=2co{s}^2(\frac{x}{2})-1;sin形式更重要,比较接近(容易使用)第一重要极限) \\ \underset{x\to 0}{\lim }\frac{1-cos(x)}{x^2}=\underset{x\to 0}{\lim }\frac{2si{n}^2(\frac{x}{2})}{x^2}=\underset{x\to 0}{\lim }\frac{2si{n}^2(\frac{x}{2})}{4(\frac{x}{2}{)}^2} \\ =\underset{x\to 0}{\lim }\frac{1}{2}(\frac{sin(\frac{x}{2})}{\frac{x}{2}}{)}^2=\frac{1}{2} \\ \therefore \underset{x\to 0}{\lim }\frac{1-cos(x)}{\frac{1}{2}{x}^2}=1 \end{gathered}$$

稍复杂的等价无穷小

$(1+x{)}^a-1\sim ax$

• 前面证明过的两个等价无穷小做替换,来证明稍微复杂的等价无穷小

根据对数的含义&性质:

$$\begin{gathered} {a}^{lo{g}_{a}b}=b \\ ln{x}^n=n\cdot ln(x) \\ (1+x{)}^a=e^{lo{g}_e(1+x{)}^a}=e^{ln(1+x{)}^a}=e^{a\cdot ln(1+x)} \end{gathered}$$

• 从而需要被证明的命题变为:

$$\begin{gathered} e^{a\cdot ln(1+x)}-1\sim x \\ 或者说:(1+x{)}^a-1=e^{a\cdot \ln (x+1)}-1\sim a\cdot \ln (x+1) \end{gathered}$$

$$\begin{gathered} \underset{x\to 0}{\lim }\frac{e^{a\cdot ln(1+x)}-1}{x} \\ ★利用前面证明的ln(x+1)\sim x,将分母进行替换(等价无穷小替换定理) \\ 从而得到形如另一个等价无穷小的形式: \\ \underset{x\to 0}{\lim }\frac{e^x-1}{x}=1 \\ ★或者,替换分子(分子整体是符合e^x-1(e^x-1\sim x的形式)), \\ 这里x取值为表达式x=a\cdot \ln (x+1),从而: \\ (1+x{)}^a-1=e^{a\cdot \ln (x+1)}-1\sim a\cdot \ln (x+1) \\ 现在,\underset{x\to 0}{\lim }\frac{(1+x{)}^a-1}{x}=\underset{x\to 0}{\lim }\frac{a\cdot \ln (x+1)}{x}=\underset{x\to 0}{\lim }a\frac{ln(x+1)}{x}=a \\ 从而: \\ \underset{x\to 0}{\lim }\frac{(x+1{)}^a-1}{ax}=1 \end{gathered}$$

或者使用换元+配凑的方法

$$\begin{gathered} 令t=(1+x{)}^a-1;即,(1+x{)}^a=t+1 \\ 则\ln (1+x{)}^a=\ln (t+1) \\ =\underset{x\to 0}{\lim }\frac{(1+x{)}^a-1}{x}\frac{ln(1+x{)}^a}{ln(1+x{)}^a} \\ =\underset{x\to 0}{\lim }\frac{(1+x{)}^a-1}{x}\frac{a\cdot ln(1+x)}{ln(1+x{)}^a} \\ =\underset{x\to 0}{\lim }\frac{(1+x{)}^a-1}{ln(1+x{)}^a}\frac{a\cdot ln(1+x)}{x} \\ =\underset{t\to 0}{\lim }\frac{t}{ln(t+1)}\cdot \underset{x\to 0}{\lim }\frac{a\cdot ln(1+x)}{x} \\ =1\times a=a \end{gathered}$$

小结

• 上述公式中,有-1的一般都是为了使用$1^{\infty }$的重要极限(第二重要极限e)
• 其中+1不换元既可以靠近第二重要不等式
• -1换元后转换为＋1

等价无穷小之间的比较

无穷小之间不总是可以比较的(有些无穷小没有高低阶之分,也没有同阶可言)

例如:

$$\begin{gathered} \{\begin{array}{l}f(x)=xsin(\frac{1}{x})\\ g(x)=x\\ h(x)=sin(\frac{1}{x})\end{array} \\ \underset{x\to 0}{\lim }\frac{xsin(\frac{1}{x})}{x}=\underset{x\to 0}{\lim }sin(\frac{1}{x}) \\ 显然,h(x)的极限不存在(但f(x)\&g(x)单独的时候,都是x\to 0过程的无穷小量.) \end{gathered}$$

常见无穷大的比较

• 无穷大乘以无穷大得到无穷大

• 无穷大+无穷大没有定论(鉴于无穷大区分正无穷和负无穷)

• $无穷大+有界\Rightarrow 无穷大$

• $无穷小乘以有界\Rightarrow 无穷小$

• $无穷大乘以有界\nRightarrow 无穷大$

  • $n\cdot 0=0$

  • 譬如,$f(x)=x;g(x)=0;h(x)=f(x)g(x)=0$

无穷大量(变量)&无界变量的关系

• 无穷大量可以推出无界
  • 但是无界不可以推出无穷大量
  • $\forall M>0,\exists N>0,|X_N|>M\Rightarrow 无界变量$
  • $\forall M>0,\exists N>0,n>N时,恒有|X_N|>M\Rightarrow 无穷大$
  • 例如 { a n } = 1 , 0 , 3 , 0 , 5 , 0 , ⋯ , 0 , 2 k + 1 \set{a_n}=1,0,3,0,5,0,\cdots,0,2k+1 {an​}=1,0,3,0,5,0,⋯,0,2k+1
    • 是无界变量但不是无穷大

$$f(x)=x+(-1{)}^{n}x$$

综合例题

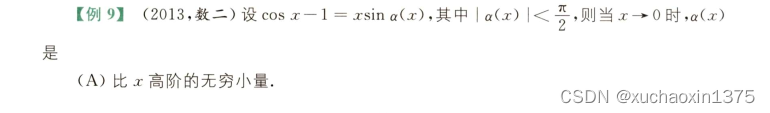
• 复合函数和无穷小量之间的比较

  • 用到的等价无穷小包括:

    $$\begin{gathered} cosx-1\sim \frac{-1}{2}{x}^2;(1-cosx\sim \frac{1}{2}{x}^2) \\ sin(x)\sim x;(类似的sin(\alpha (x))\sim \alpha (x)) \end{gathered}$$

  • 复合函数需要考虑外层函数的定义域和内层函数的值域之间的制约

  • 本题中

$$\begin{gathered} 根据等价无穷小,\underset{x\to 0}{\lim }h(x)=\underset{x\to 0}{\lim }sin(\alpha (x))=-\frac{1}{2}, \\ h(x)=sin(\alpha (x))和y=x是x\to 0的同阶无穷小从而,\underset{x\to 0}{\lim }h(x)=0 \\ |\alpha (x)|<\frac{\pi }{2}为了更加通俗的理解该条件,去掉绝对值得到: \\ -\frac{\pi }{2}<\alpha (x)<\frac{\pi }{2} \\ 指出了函数\alpha (x)的取值范围 \\ 记:u=\alpha (x) \\ \underset{x\to 0}{\lim }u=u_0 \\ 根据三角坐标单位圆可知\underset{u\to k\pi }{\lim }sin(u)= \\ \underset{x\to 0}{\lim }sin(\alpha (x))=\underset{u\to u_0}{\lim }sin(u)=0 \\ \because \underset{u\to k\pi }{\lim }sin(u)=0 \\ \therefore u_0=k\pi \\ 根据\alpha (x)的值域,可知,u_0⩽\frac{\pi }{2} \\ \therefore k=0 \\ (u_0=0,即\underset{x\to 0}{\lim }\alpha (x)=u_0=0), \end{gathered}$$