---

前言

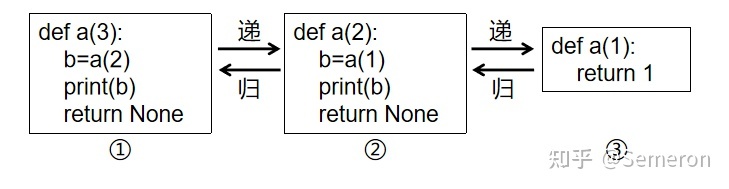
递归，很常见的一种算法，在初学的时候我们都会用递归来解决斐波那契数列，但递归本身有非常大的缺陷，就是时间和空间占用都非常大，在进阶学习后，换种方法来代替递归。

---

一、递归实现斐波那契

import datetime# 递归实现斐波那契
def feiBo(n):if n <= 2:return 1return feiBo(n - 1) + feiBo(n - 2)if __name__ == '__main__':n = int(input())# 记录开始时间starttime = datetime.datetime.now()print(feiBo(n))# 使用开始时间减去结束时间便可得出运行时间print((starttime - datetime.datetime.now()).seconds)

这是用递归实现的斐波那契，我们输入一个20来看看运算时间，如下图：

图中红色的为结果，绿色的为运行时间

二、优化后的斐波那契

代码如下：

import datetime# 优化
def feiBo(n):a = b = 1for i in range(2, n + 1):a, b = b, a + breturn aif __name__ == '__main__':n = int(input())# 记录开始时间starttime = datetime.datetime.now()print(feiBo(n))# 使用开始时间减去结束时间便可得出运行时间print((starttime - datetime.datetime.now()).seconds)

利用一个for循环来替代递归，无论是时间复杂度还是空间复杂度都远远小于递归，看看同样输入20，运行时间对比

可以看出是0，速度是非常非常快的，当输入200时，运行时间一样，可见运行速度是递归的10倍

---

总结

能不用递归的就不要使用递归，递归适合初学者，当学的比较深的时候，递归就不能满足我们的一些需求了