写在前面

学了一年的数字签名方案，一直都在一个点进行专研，虽然还是有所收获，总感觉还差点感觉，上了一年研究生，还没有对数字签名有整体了解。导师建议我从点到面，本来想写一篇综述之类的，看了看大佬写的综述，数字签名真的种类繁多，而且自己能力有限，写综述实在不知道从哪里下手，因此就想在自己博客上写写签名那些事，争取一周更一个数字签名算法，希望通过这样子方式，可以对数字签名有较深了解，也希望可以结交志趣相投的朋友一起探讨（本人菜鸟，求抱大腿）。

数字签名作用

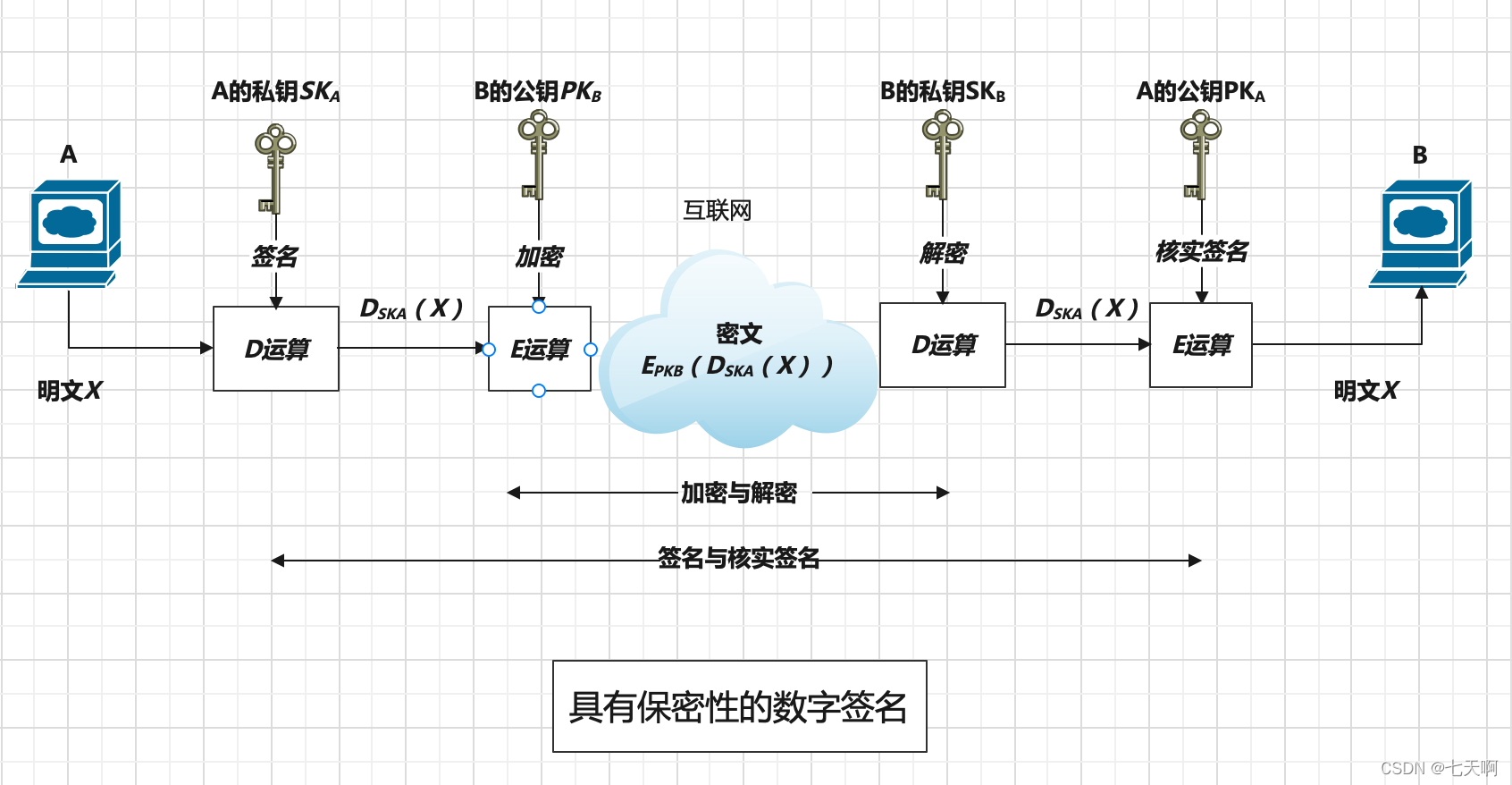
数字签名，本质上就是一种签名方式。古代人以手写或者印章，指模等方式进行签名，表示自己对签名的内容了解且负有责任，当出现矛盾纷争的时候可以作为证据起到法律责任（不知为啥想到了卖身契），随着计算机发展，要求我们对数字文档进行签名认证，如何让我们的签名如同手写印章那样合法有效？数字签名技术便应运而生。
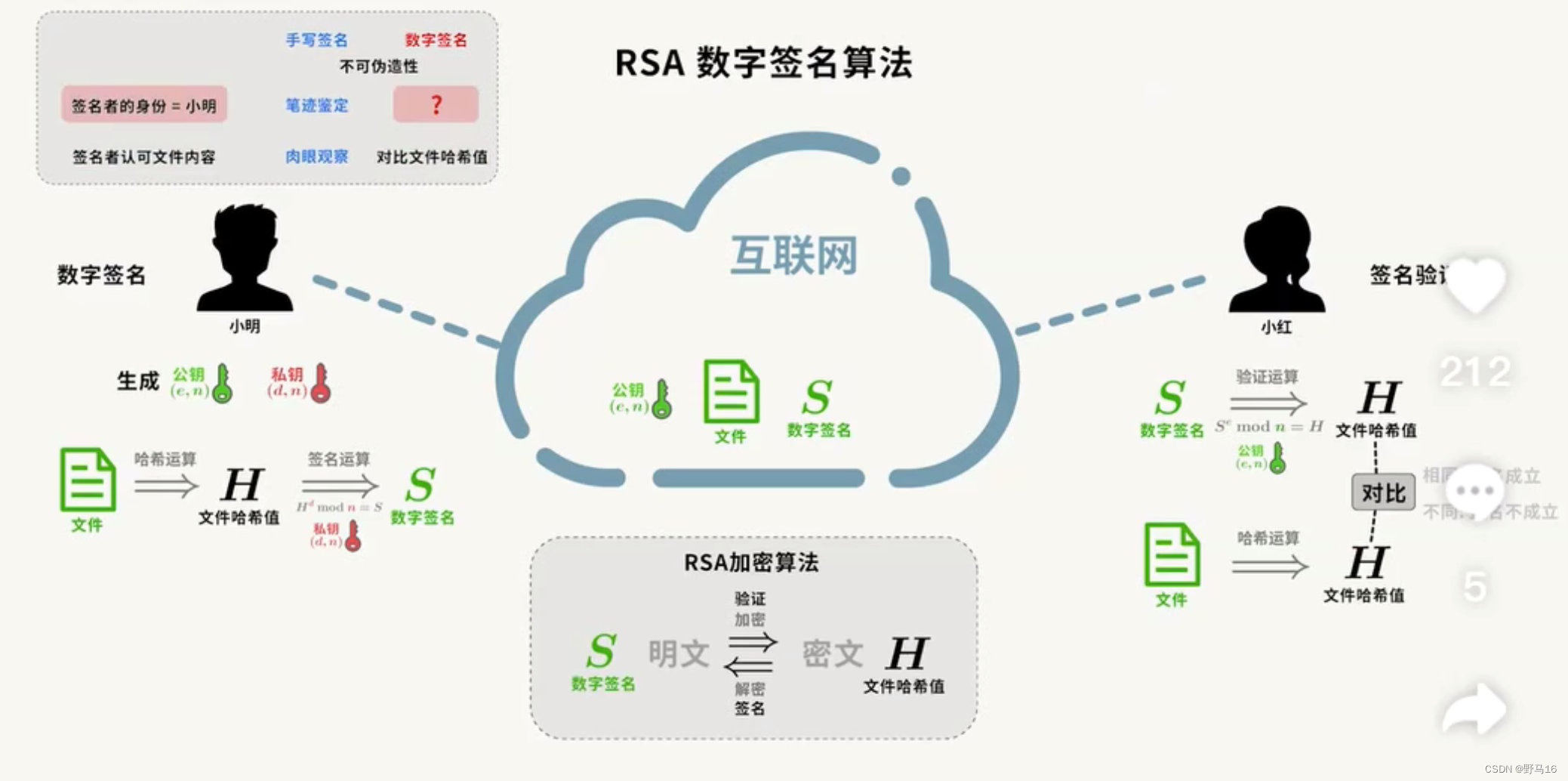
数字签名技术大多使用公钥密码机制，最简单的构造即签名者用自己私钥进行签名，任意验证者使用签名者的公钥进行验证。根据公钥密码体制可知，已知公钥求私钥是困难的，因此只要验证通过，就可以认为签名有效，因此数字签名具有保证签名者身份的真实性，签名内容完整性以及一旦验证通过，签名不可抵赖性（概括为数字签名的三个特性：真实性，完整性与不可抵赖性）。

数字签名发展史

1976年，Whitfield与Martin Hellman发表历史性文章[1],提出数字签名的概念。
1978年，发表RSA数字签名方案。RSA是一种很经典的数字签名方案，在现实生活中仍有很大的应用。迄今为止，对RSA的攻击已经很多，但都没有对它构成真正的威胁。
1978年，Rabin发表了一次性签名方案（OTS）[2]一次性签名方案实现简单，甚至可以直接用部分密钥（与身份有关）作为签名。每个密钥对仅加密1bit，安全性高。缺点是成本高，效率慢。为了提高效率，提出Merkle数字签名方案。
1984年，Elgamal发表基于离散对数问题的Elgamal数字签名算法[3]
1984年，Adi Shamir提出基于身份的密码技术（IBC），且给出了第一个基于身份的数字签名方案.基于身份的密码也称为基于标识的密码。
1986年Amos Fiat和Adi Shamir提出Fiat-Shamir变换[4]，该变换可以将一大类身份认证转化为数字签名算法。(主要应用之一，可以把交互式零知识证明转化为非交互式，化简算法，提高效率,在数字签名算法中应用广泛)
1991年NIST发表数字签名算法DSA，是对Elgamal数字签名算法的变形
2002年ChoonCha，JungHee Cheon等利用双线性对构造短签名算法。
2017年NIST征集后量子公钥算法标准化工作，后量子数字签名方案不断得到重视
2008年Gentry,Peikert等人提出了第一个高效安全的格签名方案[5]
2001年，曾贵华教授提出了第一个仲裁量子签名协议(AQS)[6]

带属性的数字签名

简单功能的数字签名方案已经不能满足一些特殊需求，比如电子现金，电子选取，交通等领域应用，使得数字签名功能不断得到完善，现介绍几个带属性的数字签名技术。
（1）盲签名：1982年David Chaum提出盲签名概念。盲签名是相对于一般的数字签名而言的概念，是指签名人员虽然对某个消息签了名，但他并不知道所签消息的具体内容，也就是说对签名人而言，消息被盲化处理过。签名的有效性是指可以在消息去盲以后公开验证。
（2）多重签名：多重数字签名即为多人同时对一份数字分档进行签名。多重数字签名技术有很多应用场景，比如，夫妻共同财产的支配问题，只有两者均同意才可以进行财产支配。多重机制可用于对于签名有需求且对长度有敏感的应用。与多重签名类似的签名机制为聚合签名。聚合签名分为通用聚合签名与顺序聚合签名两种。
（3）门限签名：提到门限签名，不得不提秘密共享技术。很多门限签名都是有秘密共享机制转化而成。门限签名是普通数字签名的一个重要分支，是门限秘密共享技术和数字签名的一种结合。1991年，Desmedt-Frankel首次提出了(t,n)门限签名方案。(t,n)门限签名方案是指由n个成员组成一个签名群体，该群体有一对公钥和私钥，群体内大于等于t个合法、诚实的成员组合可以代表群体用群私钥进行签名，任何人可利用该群体的公钥进行签名验证。这里t是门限值，只有大于等于t个合法成员才能代表群体进行签名，群体中任何个或更少的成员不能代表该群体进行签名，同时任何成员不能假冒其他成员进行签名。采用门限签名方式可以实现权力分配，避免滥用职权。
…未完待续

RSA数字签名方案

第一个数字签名方案，我选择了比较经典的RSA数字签名。在介绍这个签名之前，首先想先介绍一下RSA加解密算法：
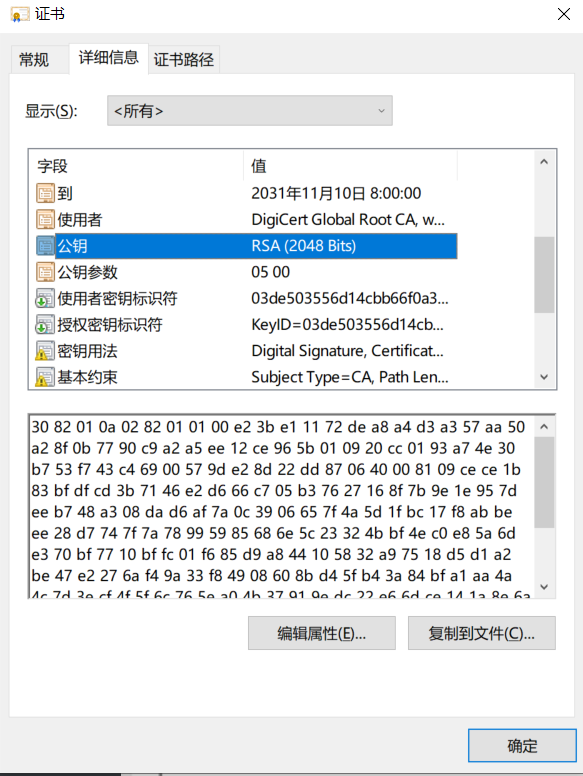
RSA公钥算法（基于大整数分解难题）
（1）选取两个不同大素数p,q
（2）计算n=pq,$\phi (n)=\left(p-1\right)\left(q-1\right)$,其中$\phi (n)$是欧拉函数。
（3）随机选取整数e作为公钥，要求满足$\left(e,\phi \left(n\right)\right)=1$
（4）采用欧几里得算法计算私钥d，使得ed=1mod$\phi (n)$。
e,n是公钥，d是私钥。p,q,$\phi (n)$可销毁不可公开
RSA签名算法
最简单的RSA签名算法即私钥签名，公钥验证，具体流程如下：
（1）密钥对的产生(e,d),把e传输给验证者。
（2）对消息M进行处理，求其摘要，公开摘要算法。
（3）用户用自己私钥对摘要进行加密处理后，把摘要以及原文发送给验证者
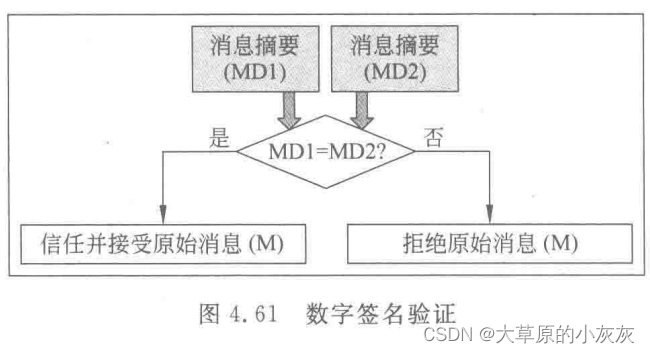
（4）验证者用对方公钥进行解密，得到摘要，计算M的摘要，看看两个摘要是否一致，一致签名成功，否则失败。
这次就先介绍到这里，如有错误望指正！

参考文献
[1] Diffie W., Hellman M. (1976) New Directions in
Cryptography. IEEE Transactions on Information Theory.
22 (6): 644.
[2]Rivest R., Shamir A., Adleman L. (1978) A Method
for Obtaining Digital Signatures and Public-Key
Cryptosystems. Communications of the ACM. 21 (2):
120–126
[3]ElGamal T. (1985) A Public Key Cryptosystem and
a Signature Scheme Based on Discrete Logarithms.
Advances in Cryptology. CRYPTO 1984. Lecture Notes in Computer Science, vol 196. Springer, Berlin,
Heidelberg.
[4]Fiat A., Shamir A. (1987) How To Prove Yourself:
Practical Solutions to Identification and Signature
Problems. Advances in Cryptology — CRYPTO’ 86.
CRYPTO 1986. Lecture Notes in Computer Science, vol
263. Springer, Berlin, Heidelberg.
[5] Craig Gentry, Chris Peikert, Vinod Vaikuntanathan. Trapdoors for hard lattices and new cryptographic constructions. In the 40th Annual ACM Symposium on Theory of Computing. ACM, 2008, 197-206.
[6]Zeng G, Keitel C H. Arbitrated quantum-signature scheme[J]. Physical Review A, 2002, 65(4): 042312.