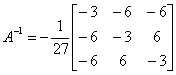复数矩阵求逆的 C 语言程序

article/2025/9/20 22:15:12

关于复数矩阵求逆，如果使用 MATLAB，就非常简单。我们先用一个 MATLAB 的例子来说明，等会要将 C 语言的程序和 MATLAB 的程序进行对比。

close all;
clear all;
clc;%定义矩阵a为复数矩阵
a = [[4+2*i,3+1*i,4+3*i,5+5*i];[1+7*i,8+2*i,2+2*i,9+3*i];[4+4*i,5+6*i,1+7*i,7+2*i];[6+1*i,7+8*i,1+4*i,2+5*i]];a_real = real(a); %求矩阵实部
a_imag = imag(a); %求矩阵虚部
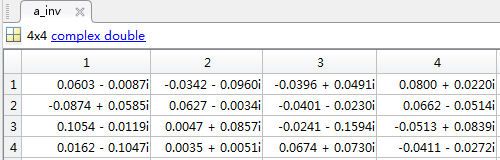
a_inv = inv(a);   %求矩阵的逆

可以看到 a_inv 是这样的：
MATLAB求解a_inv
下面列出 C 语言的矩阵求逆的代码。由于VS2012中不能使用 complex.h，我们在这里将复数矩阵的实部和虚部分开定义，数值和上面定义的 a 一样。

a_real[0][0] = 4; a_real[0][1] = 3; a_real[0][2] = 4; a_real[0][3] = 5;
a_real[1][0] = 1; a_real[1][1] = 8; a_real[1][2] = 2; a_real[1][3] = 9;
a_real[2][0] = 4; a_real[2][1] = 5; a_real[2][2] = 1; a_real[2][3] = 7;
a_real[3][0] = 6; a_real[3][1] = 7; a_real[3][2] = 1; a_real[3][3] = 2;a_imag[0][0] = 2; a_imag[0][1] = 1; a_imag[0][2] = 3; a_imag[0][3] = 5;
a_imag[1][0] = 7; a_imag[1][1] = 2; a_imag[1][2] = 2; a_imag[1][3] = 3;
a_imag[2][0] = 4; a_imag[2][1] = 6; a_imag[2][2] = 7; a_imag[2][3] = 2;
a_imag[3][0] = 1; a_imag[3][1] = 8; a_imag[3][2] = 4; a_imag[3][3] = 5;

完整代码及其注释如下：

#include <stdio.h>
#include <stdlib.h>
#include <memory.h>#define N 4
#define DEBUG 1         //debug label，0即不打印相关结果，非0打印相关输出结果//计算实数矩阵的逆
void matrix_inverse_LU(double a[][N],double a_inverse[N][N])
{double  l[N][N], u[N][N];double  l_inverse[N][N], u_inverse[N][N];//double  a_inverse[N][N];int i, j, k;double  s, t;memset(l, 0, sizeof(l));memset(u, 0, sizeof(u));memset(l_inverse, 0, sizeof(l_inverse));memset(u_inverse, 0, sizeof(u_inverse));memset(a_inverse, 0, sizeof(u_inverse));for (i = 0; i < N;i++)       //计算l矩阵对角线{l[i][i] = 1;}for (i = 0;i < N;i++){for (j = i;j < N;j++){s = 0;for (k = 0;k < i;k++){s += l[i][k] * u[k][j];}u[i][j] = a[i][j] - s;      //按行计算u值}for (j = i + 1;j < N;j++){s = 0;for (k = 0; k < i; k++){s += l[j][k] * u[k][i];}l[j][i] = (a[j][i] - s) / u[i][i];      //按列计算l值}}for (i = 0;i < N;i++)        //按行序，行内从高到低，计算l的逆矩阵{l_inverse[i][i] = 1;}for (i= 1;i < N;i++){for (j = 0;j < i;j++){s = 0;for (k = 0;k < i;k++){s += l[i][k] * l_inverse[k][j];}l_inverse[i][j] = -s;}}#if DEBUGprintf("test l_inverse:\n");for (i = 0; i < N; i++){for (j = 0; j < N; j++){s = 0;for (k = 0; k < N; k++){s += l[i][k] * l_inverse[k][j];}printf("%f ", s);}putchar('\n');}
#endiffor (i = 0;i < N;i++)                    //按列序，列内按照从下到上，计算u的逆矩阵{u_inverse[i][i] = 1 / u[i][i];}for (i = 1;i < N;i++){for (j = i - 1;j >=0;j--){s = 0;for (k = j + 1;k <= i;k++){s += u[j][k] * u_inverse[k][i];}u_inverse[j][i] = -s / u[j][j];}}#if DEBUGprintf("test u_inverse:\n");for (i = 0;i < N;i++){for (j = 0;j < N;j++){s = 0;for (k = 0;k < N;k++){s += u[i][k] * u_inverse[k][j];}printf("%f ",s);}putchar('\n');}
#endiffor (i = 0;i < N;i++)            //计算矩阵a的逆矩阵{for (j = 0;j < N;j++){for (k = 0;k < N;k++){a_inverse[i][j] += u_inverse[i][k] * l_inverse[k][j];}}}#if DEBUGprintf("test a:\n");for (i = 0; i < N; i++){for (j = 0; j < N; j++){s = 0;for (k = 0; k < N; k++){s += a[i][k] * a_inverse[k][j];}printf("%f ", s);}putchar('\n');}
#endif
}//矩阵乘法，由于这里计算的是长度N的方阵，所以实际上ROW,MID,COL的值都是N
void MulMatrix(const double (*arr1)[N], const double (*arr2)[N], int ROW, int MID, int COL, double (*arr3)[N])
{double sum=0.0;int i,j,m;for (i = 0; i<ROW; i++){for (j = 0; j<COL; j++){sum = 0.0;for (m = 0; m<MID; m++){sum = sum + arr1[i][m] * arr2[m][j];}arr3[i][j] = sum;}}
}//矩阵加法
void PlusMatrix(const double (*arr1)[N], const double (*arr2)[N], int ROW, int COL, double (*arr3)[N])
{int i,j;for(i=0;i<N;i++)//控制行{for(j=0;j<N;j++){arr3[i][j]=arr1[i][j]+arr2[i][j];}}
}//矩阵减法
void MinusMatrix(const double (*arr1)[N], const double (*arr2)[N], int ROW, int COL, double (*arr3)[N]) 
{int i,j;for(i=0;i<N;i++)//控制行{for(j=0;j<N;j++){arr3[i][j]=arr1[i][j]-arr2[i][j];}}
}void main()
{int i, j, k;double a[N][N]; //N表示矩阵维度，为4double a_real[N][N];double a_imag[N][N];double Ainv[N][N],Binv[N][N],BAinv[N][N],BAinvB[N][N],A_P_BAinvB[N][N],A_P_BAinvB_inv[N][N],AinvB[N][N],AinvB_A_P_BAinvB[N][N],AinvB_A_P_BAinvB_inv[N][N];//将a矩阵的实部和虚部分开定义a_real[0][0] = 4;a_real[0][1] = 3;a_real[0][2] = 4;a_real[0][3] = 5;a_real[1][0] = 1;a_real[1][1] = 8;a_real[1][2] = 2;a_real[1][3] = 9;a_real[2][0] = 4;a_real[2][1] = 5;a_real[2][2] = 1;a_real[2][3] = 7;a_real[3][0] = 6;a_real[3][1] = 7;a_real[3][2] = 1;a_real[3][3] = 2;a_imag[0][0] = 2;a_imag[0][1] = 1;a_imag[0][2] = 3;a_imag[0][3] = 5;a_imag[1][0] = 7;a_imag[1][1] = 2;a_imag[1][2] = 2;a_imag[1][3] = 3;a_imag[2][0] = 4;a_imag[2][1] = 6;a_imag[2][2] = 7;a_imag[2][3] = 2;a_imag[3][0] = 1;a_imag[3][1] = 8;a_imag[3][2] = 4;a_imag[3][3] = 5;//这些计算公式来源于这里：https://wenku.baidu.com/view/2de4c1bc284ac850ad024244.htmlmatrix_inverse_LU(a_real,Ainv);matrix_inverse_LU(a_imag,Binv);MulMatrix(a_imag,Ainv,N,N,N,BAinv);MulMatrix(BAinv,a_imag,N,N,N,BAinvB);PlusMatrix(a_real,BAinvB,N,N,A_P_BAinvB);matrix_inverse_LU(A_P_BAinvB,A_P_BAinvB_inv);MulMatrix(Ainv,a_imag,N,N,N,AinvB);MulMatrix(AinvB,A_P_BAinvB_inv,N,N,N,AinvB_A_P_BAinvB_inv);//最后一步要把AinvB_A_P_BAinvB_inv每个数都求相反数，也是上面链接的文献里说的for (i = 0; i < N; i++){for (j = 0; j < N; j++){AinvB_A_P_BAinvB_inv[i][j] = -AinvB_A_P_BAinvB_inv[i][j];}}//输出a的逆矩阵的实部矩阵printf("test a_inv_real:\n");for (i = 0; i < N; i++){for (j = 0; j < N; j++){printf("%f ", A_P_BAinvB_inv[i][j]);}printf("\n");}//输出a的逆矩阵的虚部矩阵printf("test a_inv_imag:\n");for (i = 0; i < N; i++){for (j = 0; j < N; j++){printf("%f ", AinvB_A_P_BAinvB_inv[i][j]);}printf("\n");}//使得窗口不要关闭getchar();
}

最后输出结果如下：
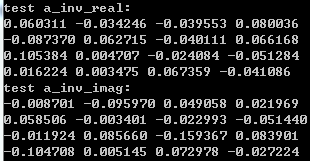
C语言输出结果
通过对比，可以发现该结果中的实部和虚部与 MATLAB 输出的结果是一致的。这证明我们的程序是正确的。


http://chatgpt.dhexx.cn/article/Ucler9yT.shtml

相关文章

科学计算器如何求矩阵的逆

科学计算器如何求矩阵的逆

大学本科买了四年的计算器不会求逆&#xff0c;到了研究生了好好研究下这个功能&#xff0c;终于终于会用了&#xff0c;以往 对着那个矩阵功能都发懵&#x1f602;&#xff0c;记录一下这个史诗无敌隐藏功能 1、进入菜单&#xff0c;点击4进入矩阵菜单 2、这里选择1定义矩阵A…
阅读更多...
matlab求一个矩阵的逆矩阵的命令,如何用MATLAB求逆矩阵

matlab求一个矩阵的逆矩阵的命令,如何用MATLAB求逆矩阵

如何用MATLAB求逆矩阵以下文字资料是由(历史新知网www.lishixinzhi.com)小编为大家搜集整理后发布的内容，让我们赶快一起来看一下吧！ 如何用MATLAB求逆矩阵 如果英文好呢，自己看目录 不好还是先看中文的教材，对matlab的框架和功能有了一定的了解后，自己也就看的懂帮助里面…
阅读更多...
matlab矩阵求逆的模块,matlab矩阵求逆矩阵

matlab矩阵求逆的模块,matlab矩阵求逆矩阵

matlab矩阵求逆矩阵 因为 所以该矩阵可逆&#xff0c;根据 &#xff0c;其中 得到 计算矩阵A每个元素的代数余子式&#xff1a; 所以 可得&#xff1a; matlab计算如下&#xff1a; >> A1[1 2 2;2 1 -2;2 -2 1] A1 1 2 2 2 1 -2 2 -2 1 >> >> >> A2in…
阅读更多...
求矩阵的逆的三种方法

求矩阵的逆的三种方法

我们知道求矩阵的逆具有非常重要的意义&#xff0c;本文分享给大家如何针对3阶以内的方阵&#xff0c;求出逆矩阵的3种手算方法&#xff1a;待定系数法、伴随矩阵法、初等变换法&#xff08;只介绍初等行变换&#xff09; 待定系数法求逆矩阵 1 首先&#xff0c;我们来看如何使…
阅读更多...
千万不能错过的Android NDK下载安装及配置

千万不能错过的Android NDK下载安装及配置

Java 语言是一个跨平台的语言&#xff0c;有着“Write Once&#xff0c;Run Anywhere”的美誉。但是却导致了它和本地交互的能力不够强&#xff0c;无法完成一些和操作系统相关的特性。 而 JNI 就是 Java Native Interface&#xff08;Java 本地接口&#xff09;&#xff0c;用…
阅读更多...
NDK在Linux下载配置以及C、C++编译配置（交叉编译）

NDK在Linux下载配置以及C、C++编译配置（交叉编译）

NDK在Linux下载配置以及C、C编译配置&#xff08;交叉编译&#xff09; 前言&#xff1a; 我们搭建好Ubutu虚拟机之后&#xff0c;通过xShell远程登录Ubutu上SSH服务器&#xff0c;在xShell上可以进行相关的编译操作了。但是我们在xShell上gcc、g编译的可执行文件只能在Linux…
阅读更多...
Android——NDK下载提示缺少toolchains问题解决

Android——NDK下载提示缺少toolchains问题解决

更新下载了最新的NDK&#xff0c;发现Android SDK报错。 No toolchains found in the NDK toolchains folder for ABI with prefix: mips64el-linux-android。 解决办法&#xff1a; 1.找到并进入下载安装的ndk目录 lydeMacBook-Pro:~ imac$ cd /Users/ly/Library/Android/sd…
阅读更多...
android ndk 下载安装(ubuntu)

android ndk 下载安装(ubuntu)

1. 下载并解压安装包 官网下载&#xff1a;https://developer.android.com/studio ndk各个版本下载地址&#xff1a;https://blog.csdn.net/u011077027/article/details/102706283 官网下载需要梯子&#xff0c;百度云盘下载&#xff1a;链接: https://pan.baidu.com/s/1Ge8fQu…
阅读更多...
Window NDK下载以及环境变量配置

Window NDK下载以及环境变量配置

作者介绍&#xff1a;铸梦xy。IT公司技术合伙人&#xff0c;IT高级讲师&#xff0c;资深Unity架构师&#xff0c;铸梦之路系列课程创始人。 第一种 NDK下载安装步骤一 NDK环境变量配置步骤一 测试NDK配置 第二种 支持编译c ninja 前言 NDK是开发者必不可少的一部分&#xff0c…
阅读更多...
3、NDK下载、安装

3、NDK下载、安装

文章目录 一、下载NDK二、配置环境变量三、测试 一、下载NDK 官网下载地址:https://developer.android.google.cn/ndk/downloads/,选择自己相应的版本&#xff0c;下载解压。(我安装在D:\utils\android-ndk-r21d) 特别注意&#xff1a;安装路径不要有中文和空格 二、配置环境…
阅读更多...
【Android NDK 开发】Android NDK 下载 ( 下载指定历史版本 NDK | Android NDK r10e - 2015 年 5 月 )

【Android NDK 开发】Android NDK 下载 ( 下载指定历史版本 NDK | Android NDK r10e - 2015 年 5 月 )

文章目录 一、下载指定历史版本 NDK 一、下载指定历史版本 NDK 进入到 ndk 下载的 " 修订历史记录 " 页面 https://developer.android.google.cn/ndk/downloads/revision_history ; 在该页面中 , 有 Android NDK r1&#xff08;2009 年 6 月&#xff09;~ Android N…
阅读更多...
android ndk官网下载地址,android ndk下载

android ndk官网下载地址,android ndk下载

android ndk&#xff0c;在SDK前加上原生二字就是Native Development Kit&#xff0c;支持32位和64位使用&#xff0c;有需要的朋友可以来本站下载。 【使用方法】 1、打开Eclipse&#xff0c;点Window->Preferences->Android->NDK,设置NDK路径&#xff0c;例如Shamoo…
阅读更多...
【NDK】Android NDK下载安装教程

【NDK】Android NDK下载安装教程

目录 Android NDK下载安装教程 不积跬步&#xff0c;无以至千里&#xff1b;不积小流&#xff0c;无以成江海。要沉下心来&#xff0c;诗和远方的路费真的很贵&#xff01; Android NDK下载安装教程 打开Android Studio的 SDK Manager。 选中SDK Tools&#xff0c;选择要下载…
阅读更多...
android studio 如何下载指定版本的NDK

android studio 如何下载指定版本的NDK

安装及配置 NDK 和 CMake | Android 开发者 | Android Developers 如果官方文档看不懂的&#xff0c;就看我写的口水话版本吧&#xff1b; 1、AS打开SDK、NDK下载的那个对话框&#xff0c;如图&#xff1a; 2、非常关键的一步&#xff0c;默认情况下选项的子项未展开&…
阅读更多...
fallback method wasn‘t found

fallback method wasn‘t found

两种情况会报这个异常&#xff1a; 1、指定的降级方法 确保配置和注解都是开启了的前提下 2、全局使用的降级方法
阅读更多...
设置统一的hystrix fallback接口

设置统一的hystrix fallback接口

设置统一的hystrix fallback接口 前言Order工程改进&#xff08;将fallback方法放到类中&#xff09;&#xff1a;即设置统一的hystrix fallback接口1.不在方法上使用HystrixCommand注解2、创建回调类3、在Feign客户端中添加fallback属性4、配置文件中开启hystrix5、重新启动应…
阅读更多...
Sentinel服务熔断功能（sentinel整合ribbon+openFeign+fallback）

Sentinel服务熔断功能（sentinel整合ribbon+openFeign+fallback）

目录 1、Sentinel服务熔断功能 一、Ribbon系列 &#xff08;一&#xff09;提供者9003/9004 &#xff08;二&#xff09;消费者84 二、OpenFeign系列 三、熔断框架比较 2、规则持久化 1、Sentinel服务熔断功能 一、Ribbon系列 &#xff08;一&#xff09;提供者9003/9004 …
阅读更多...
Sentinel的blockHandler与fallback的区别

Sentinel的blockHandler与fallback的区别

一、两者区别 这里说明一下&#xff0c;笔者使用的是Alibaba的Sentinel限流降级框架&#xff0c;Sentinel提供了限流、服务降级功能&#xff0c;但是只是限制后&#xff0c;返回不可控的结果肯定是不行的&#xff0c;我们还要保证调用者在调用那些被限制的服务时候&#xff0c…
阅读更多...
Fallback函数

Fallback函数

Fallback函数的使用 特点&#xff1a; 1.无名字&#xff0c;无参数&#xff0c;无返回值 2.如果请求的方法在合约中不存在&#xff0c;则会调用fallback函数 3.对合约转账的时候&#xff0c;会自动执行fallback函数(可能会产生Reentrancy漏洞) 4.在高版本中已经将定义形式改为…
阅读更多...
sentinel1.8.1中fallback兜底方法和@RestControllerAdvice全局异常处理

sentinel1.8.1中fallback兜底方法和@RestControllerAdvice全局异常处理

环境描述&#xff0c;同上一篇文章 sentinel设置blockHandlerClass和blockHandler不生效的坑 目录 1.sentinel的blockHandler和fallback 2.RestControllerAdvice是否也可以兜底&#xff1f;&#xff1f;&#xff1f; 总结&#xff1a;二者结果相似&#xff0c;按需自取即…
阅读更多...
推荐文章

Copyright @ 2022~2023