数学建模预测模型学习（一）——灰色预测模型

article/2025/3/28 2:34:14

[1]累加生成（AGO）
举个简单的例子：{a, b, c, d, e}为原始序列，一次累加生成后的序列即{a, a+b, a+b+c, a+b+c+d, a+b+c+d+e}（n次累加生成依此类推）。
用数学表达式表示为：
$X^{(1)}(k)=\sum_{i=1}^{k}X^{(0)}(i)$ , 即累加序列中的第k个数等于原始序列前k个元素之和。
[2]加权邻值生成
设原始序列为 $X^{(0)}$ ={ $X^{(0)}$ (1), $X^{(0)}$ (2), …… $X^{(0)}$ (n) }，那么像 $X^{(0)}$ (k), $X^{(0)}$ (k-1)就是一对邻值，然后取权分别为 a 和 1-a (0<=a<=1)，那么加权邻值生成序列 $z^{(0)}$ (k)=a * $X^{(0)}$ (k) + (1-a) * $X^{(0)}$ (k-1) , (k=2,3,…n)
当a=0.5时，就称为均值生成，也称等权邻值生成。
[3]累减生成（IAGO）
它是累加生成的逆运算。一般用于把累加生成序列还原成原始序列，在累加序列求导时也有神奇的作用。
举个简单的例子：
累加生成序列为{a, a+b, a+b+c, a+b+c+d}，经累减生成即可生成原始序列{a, b, c, d}。具体过程用数学表达式表示为：
$X^{(0)}$ (k) = $X^{(1)}$ (k) - $X^{(1)}$ (k-1) , (k=2,3,……n)。即第k个原始序列元素等于累加生成序列中第k个减去第k-1个。

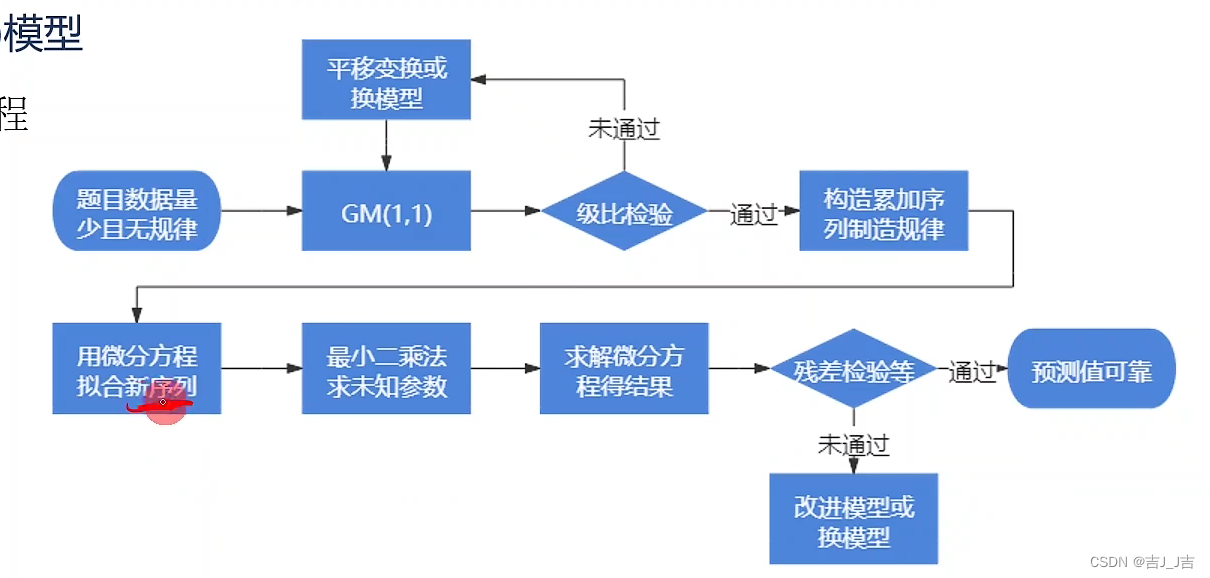
三、GM(1,1)模型：

1、级比分析：

级比分析是判断灰度模型GM(1,1)能否用于解决某个问题的关键。主要是在最开始搭建模型时对数据进行级比检验。其中的复杂原理这里不多做解释，用法很简单。
（1）先计算λ(k)= $X^{(0)}$ (k-1) / $X^{(0)}$ (k), (k=2,3,…n)
（2）如果λ(k)在区间 $\left ( e^{-\frac{2}{n+1}}, e^{\frac{2}{n+1}}\right )$ 内，则说明灰度模型GM(1,1)适用于该数据集。否则要对数据进行变换，例如可以做平移变换，给每个数据加上一个常数c，通过改变c的取值来试探是否可以通过变换使数据能够适用GM(1,1)。如果成功了，把最后的解减去c即我们最终要求的答案；如果失败了，说明该问题不适合用灰度模型GM(1,1)求解。

2、GM(1,1）:

第一步，根据已知原始数据 $X^{(0)}$ 用累加生成的方法生成新的序列 $X^{(1)}$ ；

第二步，画出新序列 $X^{(1)}$ 的散点图，观察其形状走势规律，用曲线进行拟合。（很多情况中，新序列得到的散点图会近似一条指数曲线）

第三步，构建常微分方程求解拟合曲线的函数表达式。（因变量为 $X^{(1)}$ 中的元素, 自变量通常是t，以实际情况为准）

微分方程的一般式为：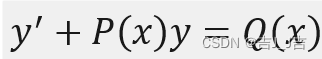
微分方程公式
因此，我们构建的拟合曲线的微分方程为：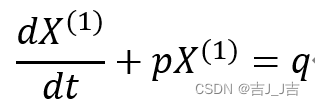
在这里插入图片描述
此时，由于一般已知的是离散数据，因此用导数d(x)的形式不是很合适，我们要把它换成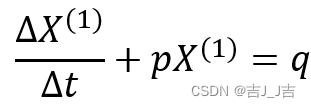

这时，我们就要用到前面累减的性质了，由于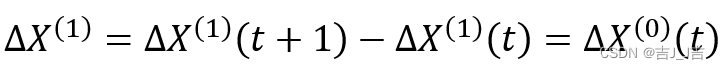

并且△t =1, 因此微分方程可以转化为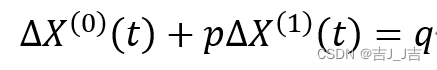

在进行适当移项变成熟悉的形式：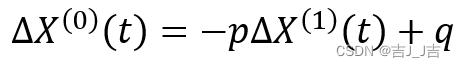
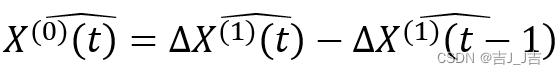
在这里插入图片描述