一、系统架构

1、大数据Lambda架构

（1）Lambda系统架构提供了一个结合实时数据和Hadoop预先计算的数据环境和混合平台, 提供一个实时的数据视图

（2）分层架构 ----- 批处理层

                a.数据不可变，可进行任何计算，可水平扩展

                b.高延迟 几分钟~几小时(计算量和数据量不同)

                c.日志收集Flume

                d.分布式存储Hadoop hdfs

                e.分布式计算Hadoop MapReduce & spark

                f.视图存储数据库 nosql (HBase/Cassandra)、Redis/memcache、Mysql

（3）分层架构 ----- 实时处理层

                a.流式处理, 持续计算

                b.存储和分析某个窗口期内的数据

                c.最终正确性(Eventual accuracy)

                d.实时数据收集 flume & kafka

                e.实时数据分析 spark streaming/storm/flink

（4）分层架构 ----- 服务层

                a.支持随机读

                b.需要在非常短的时间内返回结果

                c.读取批处理层和实时处理层结果并对其归并

（5）Lambad架构图

 2、推荐算法架构

（1）召回阶段(海选)

                a.常用算法:协同过滤(基于用户 基于物品的)

                b.基于内容 (根据用户行为总结出自己的偏好 根据偏好 通过文本挖掘技术找到内容上相似的商品)

                c.基于隐语义

(2)排序阶段

                a.召回决定了最终推荐结果的天花板, 排序逼近这个极限, 决定了最终的推荐效果

                b.CTR预估 (点击率预估 使用逻辑回归----LR算法) 估计用户是否会点击某个商品 需要用户的点击数据

（3）策略调整

二、推荐算法 

1、推荐模型构建流程

Data(数据)->Features(特征)->ML Algorithm(机器学习算法)->Prediction Output(预测输出)

（1）数据清洗/数据处理 （2）数据来源

                a.显性数据          Rating 打分 ------  Comments 评论/评价

                b.隐形数据          Order history 历史订单 ------ Cart events 加购物车

                                            Page views 页面浏览 -------Click-thru 点击 ----- Search log 搜索记录                    c.数据量/数据能否满足要求        

                d.特征工程 

                e.从数据中筛选特征         

                             一个给定的商品，可能被拥有类似品味或需求的用户购买

                             使用用户行为数据描述商品

（3）用数据表示特征将所有用户行为合并在一起 ，形成一个user-item 矩阵选择合适的算法产生推荐结果

（4）选择合适的算法 

（5）产生推荐结果

2、协同过滤推荐算法 

（1）算法思想：物以类聚，人以群分

基本的协同过滤推荐算法基于以下假设：

                     a.“跟你喜好相似的人喜欢的东西你也很有可能喜欢” ：基于用户的协同过滤推荐（User-based CF）

                      b.“跟你喜欢的东西相似的东西你也很有可能喜欢 ”：基于物品的协同过滤推荐（Item-based CF）

（2）步骤：

1. 找出最相似的人或物品：TOP-N相似的人或物品

   通过计算两两的相似度来进行排序，即可找出TOP-N相似的人或物品

2. 根据相似的人或物品产生推荐结果

   利用TOP-N结果生成初始推荐结果，然后过滤掉用户已经有过记录的物品或明确表示不感兴趣的物品

         例子：X同学爱好[足球、篮球、乒乓球]

                    Y同学爱好[网球、足球、篮球、羽毛球]，

                   可见他们的共同爱好有2个，那么他们的相似度：2/3 * 2/4 = 1/3 ≈ 0.33 来表示。

 3、相似度计算

1、计算方法

                a.数据分类

                        ------实数值(物品评分情况)

                        ------布尔值(用户的行为 是否点击 是否收藏)

                b.欧氏距离:欧氏距离的值是一个非负数, 最大值正无穷, 通常计算相似度的结果希望是 [-1,1]或[0,1]之间,一般可以使用

   

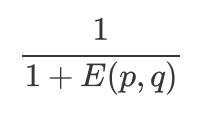
2 、杰卡德相似度&余弦相似度&皮尔逊相关系数                        

(1)余弦相似度 

        a.度量的是两个向量之间的夹角, 用夹角的余弦值来度量相似的情况

        b.两个向量的夹角为0是,余弦值为1, 当夹角为90度是余弦值为0,为180度是余弦值为-1

        c.余弦相似度在度量文本相似度, 用户相似度 物品相似度的时候较为常用

        d.余弦相似度的特点, 与向量长度无关,余弦相似度计算要对向量长度归一化, 两个向量只要方向一致,无论程度强弱, 都可以视为'相似'

（2）皮尔逊相关系数Pearson

        a.实际上也是一种余弦相似度, 不过先对向量做了中心化, 向量a b 各自减去向量的均值后, 再计算余弦相似度

        b.皮尔逊相似度计算结果在-1,1之间 -1表示负相关, 1表示正相关

        c.度量两个变量是不是同增同减

        d.皮尔逊相关系数度量的是两个变量的变化趋势是否一致, 不适合计算布尔值向量之间的相关度

（2）杰卡德相似度 Jaccard

        a.两个集合的交集元素个数在并集中所占的比例, 非常适用于布尔向量表示

        b.分子是两个布尔向量做点积计算, 得到的就是交集元素的个数

        c.分母是两个布尔向量做或运算, 再求元素和

（3）余弦相似度适合用户评分数据(实数值), 杰卡德相似度适用于隐式反馈数据(0,1布尔值)(是否收藏,是否点击,是否加购物车)

 4、基于模型的方法

（1）原理

• 根据用户与物品的潜在表现，我们就可以预测用户对未评分的物品的喜爱程度

• 把原来的大矩阵, 近似分解成两个小矩阵的乘积, 在实际推荐计算时不再使用大矩阵, 而是使用分解得到的两个小矩阵

• 用户-物品评分矩阵A是M X N维, 即一共有M个用户, n个物品 我们选一个很小的数 K (K<< M, K<<N)

• 通过计算得到两个矩阵U和矩阵V ，U是M * K矩阵 , 矩阵V是 N * K

（2）基于矩阵分解的方法

• ALS交替最小二乘

  • ALS-WR(加权正则化交替最小二乘法): alternating-least-squares with weighted-λ –regularization

  • 将用户(user)对商品(item)的评分矩阵分解为两个矩阵：一个是用户对商品隐含特征的偏好矩阵，另一个是商品所包含的隐含特征的矩阵。在这个矩阵分解的过程中，评分缺失项得到了填充，也就是说我们可以基于这个填充的评分来给用户做商品推荐了。

• SVD奇异值分解矩阵

（3） ALS方法

 

• ALS的矩阵分解算法常应用于推荐系统中，将用户(user)对商品(item)的评分矩阵，分解为用户对商品隐含特征的偏好矩阵，和商品在隐含特征上的映射矩阵。

• 与传统的矩阵分解SVD方法来分解矩阵R(R∈ℝm×n)不同的是，ALS(alternating least squares)希望找到两个低维矩阵，以 R̃ =XY 来逼近矩阵R，其中 ，X∈ℝm×d，Y∈ℝd×n，这样，将问题的复杂度由O(mn)转换为O((m+n)d)。

• 计算X和Y过程：首先用一个小于1的随机数初始化Y，并根据公式求X，此时就可以得到初始的XY矩阵了，根据平方差和得到的X，重新计算并覆盖Y，计算差平方和，反复进行以上两步的计算，直到差平方和小于一个预设的数，或者迭代次数满足要求则停止